课时作业34 空间向量在空间几何中的运用-2024-2025学年高考数学艺体生一轮复习课时作业

这是一份课时作业34 空间向量在空间几何中的运用-2024-2025学年高考数学艺体生一轮复习课时作业，文件包含课时作业34空间向量在空间几何中的运用教师版docx、课时作业34空间向量在空间几何中的运用学生版docx等2份试卷配套教学资源，其中试卷共41页， 欢迎下载使用。
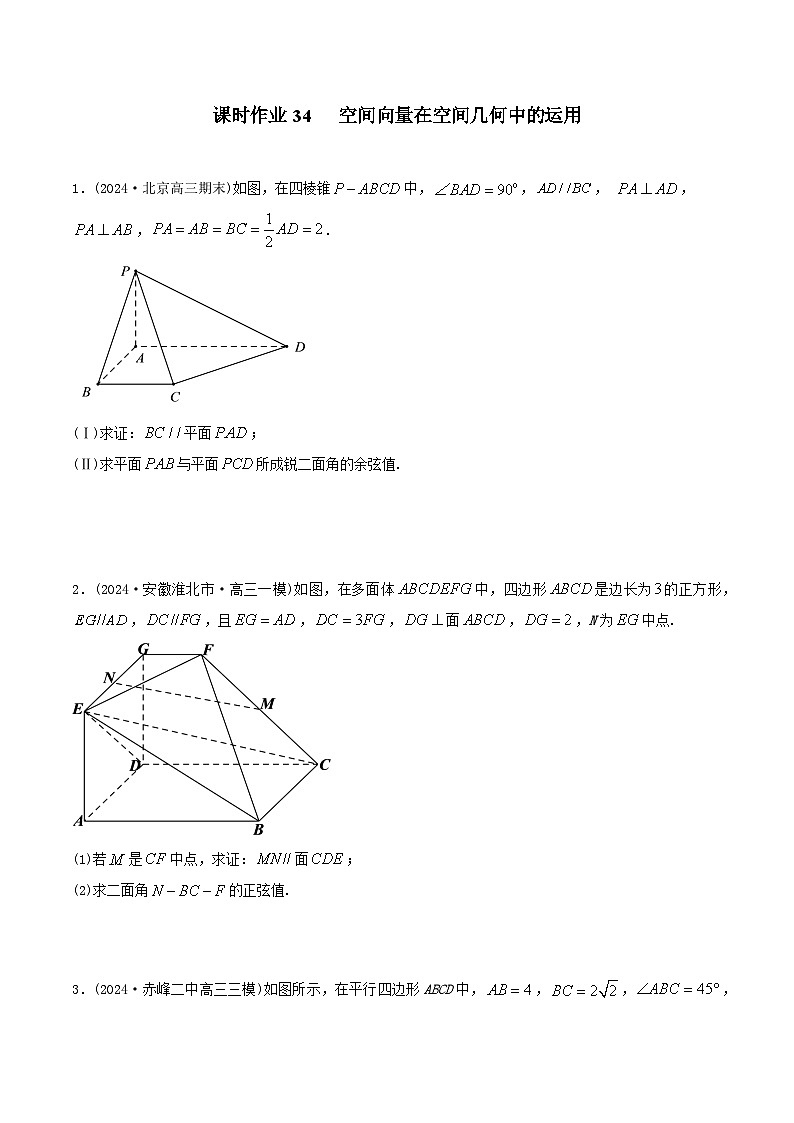
1．(2024·北京高三期末)如图，在四棱锥中，，， ，，.
(Ⅰ)求证：平面；
(Ⅱ)求平面与平面所成锐二面角的余弦值.
【答案】(Ⅰ)证明见解析；(Ⅱ).
【解析】(Ⅰ)证明：
解法1. 因为 平面 平面 所以平面
解法2.因为，，，
所以以为坐标原点，所在直线分别为轴、轴、轴，建立如图所示空间直角坐标系，则 ，
平面的法向量为 ， ，
因为 ，平面 ，所以平面；
(Ⅱ)解：因为，，
所以以为坐标原点，所在直线分别为轴、轴、轴，建立如图所示空间直角坐标系，则
所以平面的法向量为 ，
设平面的法向量为， ，
所以 ，令 ，
设平面与平面所成角为为锐角， 所以.
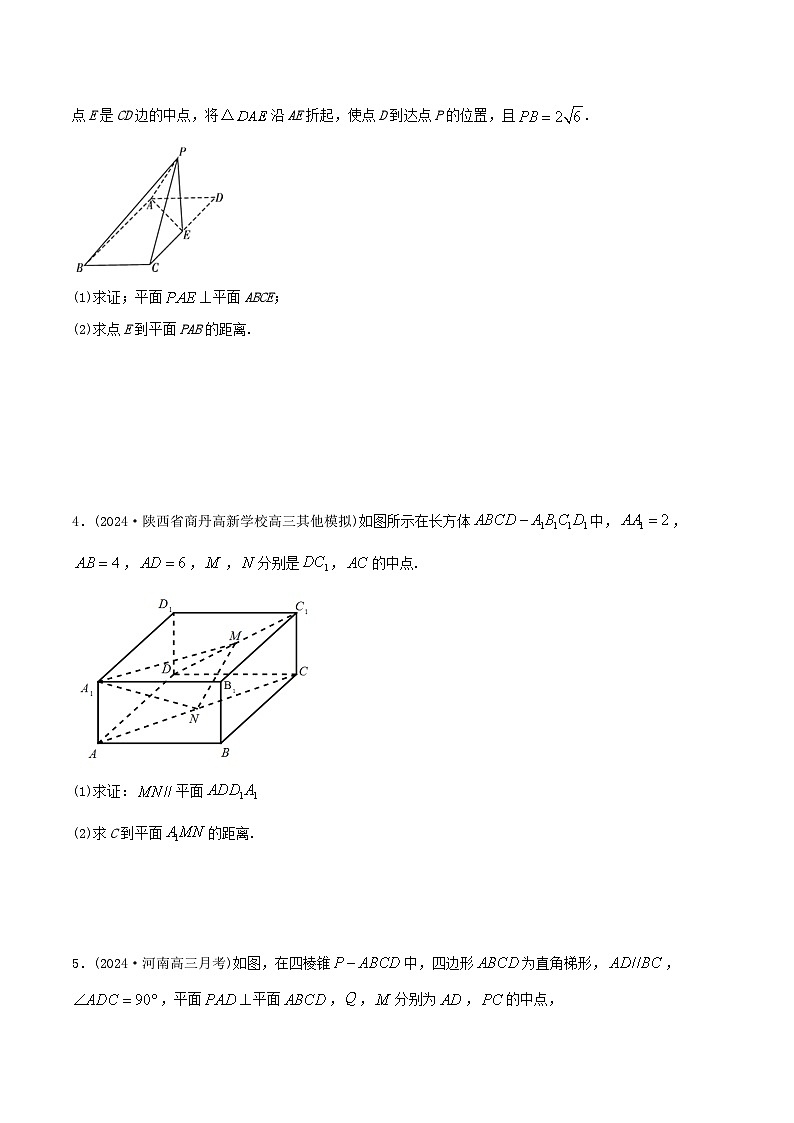
2．(2024·安徽淮北市·高三一模)如图，在多面体中，四边形是边长为的正方形，，，且，，面，，N为中点.
(1)若是中点，求证：面；
(2)求二面角的正弦值.
【答案】(1)证明见解析；(2).
【解析】(1)面，四边形是边长为的正方形，
以点为坐标原点，、、所在直线分别为、、轴建立空间直角坐标系，如下图所示：
则、、、、、、，
，，，
设平面的法向量为，由，
令，可得，，则，
，，
平面，平面；
(2)设平面的法向量为，，，
由，
令，则，，可得，
设平面的法向量为，，
由，取，则，，可得，
，.
因此，二面角的正弦值为.
3．(2024·赤峰二中高三三模)如图所示，在平行四边形ABCD中，，，，点E是CD边的中点，将沿AE折起，使点D到达点P的位置，且.
(1)求证；平面平面ABCE；
(2)求点E到平面PAB的距离.
【答案】(1)见解析；(2)
【解析】(1)∵在平行四边形ABCD中，，，，
点E是CD边的中点，将沿AE折起，
使点D到达点P的位置，且.
∴，
∴，
∵，∴，
∵，∴平面PAE，
∵平面ABCE，∴平面平面ABCE.
解：(2)∵，，，
∴，∴.
∵平面PAE，，
∴平面PAE，
∴EA，EC，EP两两垂直，
以E为原点，EA，EB，EP为x，y，轴，建立空间直角坐标系，
则，
，，
设平面PAB的法向量，
则，
取，得，
∴点E到平面PAB的距离.
4．(2024·陕西省商丹高新学校高三其他模拟)如图所示在长方体中，，，，，分别是，的中点.
(1)求证：平面
(2)求C到平面的距离.
【答案】(1)证明见解析；(2).
【解析】分别取和的中点，连接，
则且；且
所以，且，
所以四边形是平行四边形，所以，
又平面，平面，
所以平面；
(2)以为原点，分别为，建立空间直角坐标系，如图所示：
由题意，则，
又，分别是，的中点，
所以,
所以;
设平面的法向量为，则
，令，则；
所以，
设C到平面的距离为，则.
5．(2024·河南高三月考)如图，在四棱锥中，四边形为直角梯形，，，平面平面，，分别为，的中点，.
(1)求证：平面；
(2)求二面角的余弦值.
【答案】(1)证明见解析；(2).
【解析】(1)因为为的中点，，所以，
又因为，所以四边形为平行四边形.
因为，所以四边形为矩形，所以.
因为，，所以，
又因为，所以.
因为，所以平面.
(2)因为平面平面，结合(1)易知，，两两垂直，
以为原点，，，所在直线分别为，，轴建立空间直角坐标系，如图.
因为为的中点，，
因为在中，，，
所以，，，，因为为的中点，所以.
所以，，，
设平面的法向量为，
由，
令，得，，即为平面的一个法向量，
设平面的法向量为，
由，
令，得，，即为平面的一个法向量，
设二面角为，由题意，可得，
所以，
即二面角的余弦值为.
6．(2024·江苏南通市·高三期末)如图，在四棱锥中，平面，，相交于点，，已知，，.
(1)求证：平面；
(2)设棱的中点为，求平面与平面所成二面角的正弦值.
【答案】(1)证明见解析；(2).
【解析】(1)∵，，
∴，则，
∴在中，，
，
∴
∴，∴，∵平面
∴，，且都在平面，
∴平面
(2)以为轴建立空间直角坐标系，
∴，，，，，
∴，，，
设平面与平面法向量分别为，二面角为
∴，
∴，则.
7．(2024·河南高三期末)如图，直四棱柱的底面为平行四边形，，，，，是的中点.
(1)求证：平面平面；
(2)求直线和平面所成角的正弦值.
【答案】(1)证明见解析；(2).
【解析】(1)由题意可得，
所以，因此.
在直四棱柱中，
平面，平面，所以
又因为，平面，所以平面，
因为平面，所以平面平面．
(2)由(1)知，，，两两垂直，
以为原点，，，所在直线为，，轴建立如图所示的空间直角坐标系.
则，，，.
由可得，所以.
则，，，
设是平面的一个法向量，
则，
令，可得
设直线和平面所成的角为，
则.
8．(2024·江西宜春市·高三期末)如图所示，在多面体中，，，，四边形为矩形，平面平面，.
(1)证明：平面；
(2)若二面角正弦值为，求的值.
【答案】(1)证明见解析；(2).
【解析】(1)取的中点为，连接，因为且，
四边形为平行四边形，所以且，
又因为四边形为矩形，所以且，
所以四边形是平行四边形，所以，
且平面，平面，
所以平面，同可证平面，又
所以平面平面，因为平面
所以平面.
(2)由面面，知，平面，
故，，两两垂直，分别以，，的方向为轴，轴，轴的正方向建立空间直角坐标系，设，则，，，，，，
设平面的法向量为，，
则
设平面的法向量为，，
则.
，
9．(2024·陕西咸阳市·高三一模)如图，在三棱锥中，平面平面，，，，，是的中点．
(Ⅰ)求证：平面；
(Ⅱ)设点是的中点，求二面角的余弦值．
【答案】(Ⅰ)证明见解析；(Ⅱ)．
【解析】(Ⅰ)平面平面，平面平面=AC，平面，，
∴平面，
∵平面，
∴，
∵，是的中点，
∴，
∵，平面，
∴平面．
(Ⅱ)∵平面平面，平面平面=AC，平面，
∴平面，
∵平面，
∴，
以C为原点，CA，CB，CP为x，y，z轴正方向，建立如图所示的空间直角坐标系，
，，，，，，
则，，，
由(Ⅰ)知是平面的一个法向量，
设是平面的法向量，
则有，即，
令，则，，
∴，
设二面角所成角为，由图可得为锐角，
则．
10．(2024·宁夏吴忠市·高三一模)如图，在三棱锥中，平面ABC，三角形是正三角形，，点D、E、F分别为棱PA、PC、BC的中点，G为AD的中点．
(1)求证：平面BDE；
(2)求二面角的余弦值．
【解析】(1)法一：连接PF交BE于点H，连接DH，见图1:
∵E，F分别是PC，BC的中点，∴H是三角形的重心，
∴．
由已知得，∴，
又平面BDE，平面BDE，
∴平面BDE．
法二：取EC中点M，连接FM，GM，见图2:
由已知得
∴平面BDE，平面BDE，
∴平面BDE．
∵M，F分别是EC，BC的中点，
∴，又平面BDE，平面BDE，
∴平面BDE
∴，
∴平面平面BDE，又平面GFM，
∴平面BDE．
法三：在平面ABC内，以垂直于AB的直线为x轴，AB所在的直线为y轴，AP所在的直线为z轴建立空间直角坐标系，见图3，
设正三角形边长为()
则，，，
∴，
设平面BDE的法向量为，则
，，
∴，可取．
又，，
∴，∴，
即，又平面BDE，
∴平面BDE．
(2)在平面ABC内，以垂直于AB的直线为x轴，AB所在的直线为y轴，AP所在的直线为z轴建立空间直角坐标系，见图3，设正三角形边长为
则，，，
由第(1)问方法三可知，平面BDE的法向量为
设平面DEF的法向量为，
又，．
∵，，
∴，可取，
∴．
∴二面角为锐二面角，
∴二面角的余弦值为．
11．(2024·内蒙古赤峰市·高三期末)如图，四棱锥中，底面为直角梯形，其中，，面面，且，点在棱上．
(1)证明：当时，直线平面；
(2)当平面时，求二面角的余弦值．
【答案】(1)证明见解析；(2).
【解析】(1)证明：连结与交于点，连结，，
，
，，
又面，面，平面．
(2)解：平面，，是的中点，取的中点为，
平面
以，，所在的直线为，，轴建立空间直角坐标系，则
，，，，
设平面的法向量为，则
令，则，，
设平面的法向量为，则
令，则，，
二面角的余弦值为．
12．(2024·河南高三月考)如图，在四棱锥中，底面是边长为2的正方形，为的中点．
(1)求证：平面；
(2)若，，求二面角的余弦值．
【答案】(1)证明见解析；(2).
【解析】(1)连接交于，连接，则为中点，
所以为的中位线，所以，
又因为平面，平面，所以平面．
(2)在中，因为，所以，
取中点，中点，连接，，则，，
因为，，、平面，，
所以平面，又因为平面，所以，
因为，，、平面，
所以平面，又因为平面，所以，
所以，，两两垂直,
如图所示，以为原点，，，分别为轴，轴，轴建立空间直角坐标系，
则，，，，所以，
可得，，．
设平面的法向量为，
则，即，取，
设平面的法向量为，
则，即，取，
所以，
所以二面角的余弦值为．
13．(2024·安徽高三期末)在四棱锥中，平面平面，底面为直角梯形，，为线段的中点，过的平面与线段分别交于点.
(1)求证：平面；
(2)若，点G为的中点，求平面与平面所成锐二面角的余弦值.
【答案】(1)证明见解析；(2).
【解析】证明：(1)因为，且E为线段的中点，所以，又因为，所以四边形为平行四边形，所以，
又因为平面平面，所以平面，又平面平面，所以，
又，且平面平面，平面平面，所以平面，所以平面，
(2)因为为线段的中点，所以，又因为平面平面，所以平面，
以E为坐标原点，的方向为x轴正方向建立如图所示的空间直角坐标系；则，
则
设平面的法向量为，则，即
不妨令，可得为平面的一个法向量，设平面的法向量为，则，即不妨令，可得为平面的一个法向量，
设平面与平面所成的锐二面角为，
于是有；
所以平面与平面所成角的余弦值为.
14．(2024·江苏常州市·高三开学考试)如图，在四棱锥中，底面四边形是矩形，，平面平面，二面角的大小为.
(1)求证：平面；
(2)求直线与平面所成的角的正弦值.
【答案】(1)证明见解析；(2).
【解析】(1)四棱锥中，四边形是矩形，所以，
又因为平面平面，平面平面，平面
所以平面，
又因为、、平面，所以，，，
从而是二面角的平面角，
因为二面角的大小为，所以，
在中，，所以，所以，
即，
又因为，，所以平面；
(2)在底面内，过点作，垂足为，连接，
由(1)知平面，又平面，所以，
又因为，，所以平面，
从而为直线与平面所成角，
设，则，，
所以，，，
所以直线与平面所成角的正弦值为.
15．(2024·浙江绍兴市)如图，在四棱锥中，是等边三角形，平面且为中点．
(1)求证：平面；
(2)求直线与平面所成角的正弦值．
【答案】(1)证明见解析；(2)
【解析】解：(1)如图所示：
取边的中点E，连，
则三角形中位线可知：且，
由题可知：且，
且，
即四边形为平行四边形，
又平面平面，
故平面；
(2)取边的中点G，
则，且，
直线与平面所成角即为与平面所成角，
又，且易得,所以
由等体积法，，得，
与平面所成角的正弦值为，
故直线与平面所成角的正弦值为．
16．(2024·江西高三其他模拟)如图，在三棱锥中，，为的中点.
(1)证明：平面平面；
(2)求直线与平面所成角的正弦值.
【答案】(1)证明见解析(2)
【解析】(1)因为为正三角形，所以；
因为，所以.
又，平面，
所以平面.
因为平面，
所以平面平面
(2)过点P作的垂线，垂足为H，连结.
因为平面平面，又平面平面，平面，
故平面.所以直线与平面所成角为
在中，，
由余弦定得，
所以.
所以,
又，故，
即直线与平面所成角的正弦值为.
17．(2024·浙江绍兴市·高三期末)如图，三棱柱中，，在底面上的射影恰好是点，是的中点.
(1)证明：平面；
(2)求与平面所成角的正弦值.
【答案】(1)证明见解析；(2).
【解析】(1)连接与相交于，连接
由于，分别是，的中点，则
因为平面，平面，所以平面.
(2)取中点，连接，，则
因为平面，所以
又平面，，所以平面
又平面，所以平面平面，过作于
因为平面，平面平面
所以平面，连接，则即为与平面所成角
设，易知，，
由，
所以.
18．(2024·浙江绍兴市·高二期末)如图，在三棱柱中，，，，点为线段的中点．
(1)求证：．
(2)求二面角的大小．
(3)求直线与平面所成角的正弦值．
【答案】(1)证明见解析；(2)；(3).
【解析】(1)取的中点为，由于和为正三角形，则，，
又，故平面，又平面，故；
(2)由于，，故为二面角的平面角．
由于，，
由余弦定得，
从而，故二面角的大小为；
(3)如图以点原点，、所在直线为、轴建立如下图所示的空间直角坐标系．
则、、、、，
由于，，，
设平面的法向量为，
由，可得，取，则，，则，
设直线与平面所成角为，则由于，，
从而
备战高考数学成套的一轮复习，二轮复习，专题高分突破，考前回归，模拟试卷尽在备战高考QQ群722859698也可联系微信fjshuxue加入夸克网盘群3T一线老师必备资料一键转存自动更新永不过期