课时作业47 直线与曲线的最值问题-2024-2025学年高考数学艺体生一轮复习课时作业

这是一份课时作业47 直线与曲线的最值问题-2024-2025学年高考数学艺体生一轮复习课时作业，文件包含课时作业47直线与曲线的最值问题教师版docx、课时作业47直线与曲线的最值问题学生版docx等2份试卷配套教学资源，其中试卷共21页， 欢迎下载使用。
1．(2024·天津高三月考)已知椭圆的左焦点为F，离心率，长轴长为4.
(Ⅰ)求椭圆的方程；
(Ⅱ)过点F的直线l与椭圆交于M，N两点(非长轴端点)，的延长线与椭圆交于P点，求面积的最大值，并求此时直线l的方程.
【答案】(Ⅰ)；(Ⅱ)2，或.
【解析】(Ⅰ)因为椭圆长轴长为4，所以，
因为椭圆的离心率为，所以，
又，解得，
所以椭圆C的方程为；
(Ⅱ)法一：设的方程为，
联立方程组
，
，
原点到直线的距离
点P到直线的距离为 ，
，
令 ，
，
当时，面积取到最大值2，
此时，直线l的方程为或.
法二：
当k不存在时，
；
②当k存在且时，设直线方程为，
与椭圆方程联立，
可得，
显然，，
∴
，
∴，
，
令 ，
∴上式，
∴上式，
当且仅当，即时，取到最值.
综上，当时，取得最大值2.
此时，直线l的方程为或.
2．(2024·湖北武汉市)已知椭圆过点，离心率.
(1)求椭圆的方程；
(2)过点的直线与椭圆相交于，两点.
①当直线，的斜率之和为时(其中为坐标原点)，求直线的斜率；
②求的取值范围.
【答案】(1)；(2)①；②．
【解析】(1)由题意得，解得，.
设椭圆E的方程为，又因为点在椭圆E上，
所以，，
所以椭圆E的方程为；
(2)①设直线l方程为：，代入椭圆E的方程可得，
因为直线l与椭圆E有两个交点，所以，即.
设，，则，，
.
又
解得，经检验成立.所以，直线l的斜率；
②当直线l的斜率不存在时，直线l的方程为，
将代入，解得，则，，
当直线l的斜率存在时，由(2)①得
因为，所以的范围为．
综上，得的取值范围是．
3．(2024·内蒙古高三月考())已知椭圆的离心率，其左，右集点为，过点的直线与椭圆交于两点､的周长为.
(1)求椭圆的标准方程：
(2)过右焦点的直线互相垂直，且分别交椭圆于和四点，求的最小值
【答案】(1)；(2)最小值为.
【解析】(1)由椭圆的定义知，的周长为，
由，即，得
，
故椭圆的方程为：
(2)由(1)得，椭圆右焦点为，设，，，
①当直线的斜率为0，直线的斜率不存在时，
直线，此时；直线，此时；
②当直线的斜率为0，直线的斜率不存在时，；
③当直线，的斜率都存在，设直线的方程为，则直线的方程为
联立，整得
恒成立，则
同可得
则
令，则
当时，，则
所以
综上可知，，的最小值为
4．(2024·江西上高二中)已知抛物线：，过点的动直线与抛物线交于不同的两点，分别以为切点作抛物线的切线、，直线、交于点.
(1)求动点的轨迹方程；
(2)求面积的最小值，并求出此时直线的方程.
【答案】(1)；(2)1，.
【解析】(1)设，，，
则以A为切点的切线为，整得：，
同：以为切点的切线为：，
联立方程组：，解得，
设直线的方程为：，
联立方程组，整得：，
恒成立，
由韦达定得：，，故，
所以点的轨迹方程为；
(2)由(1)知：，
到直线的距离为：，
∴，
∴时，取得最小值，此时直线的方程为.
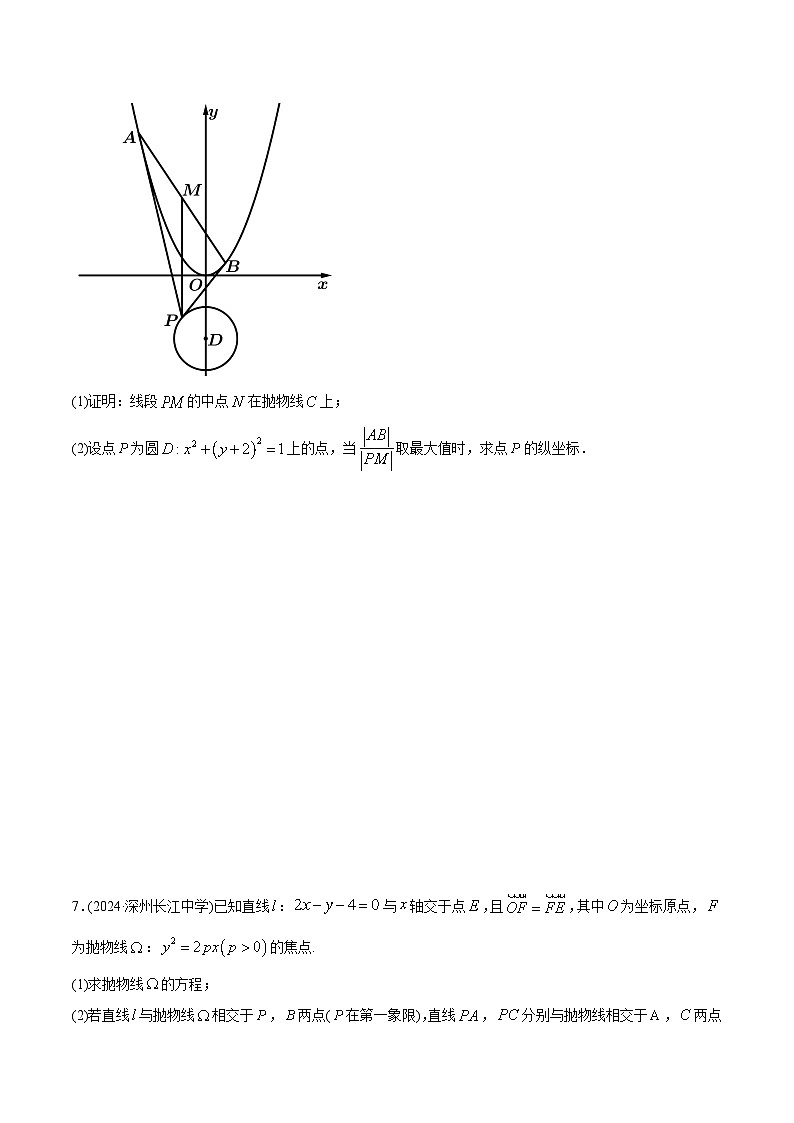
5．(2024·浙江)如图，点在抛物线外，过点作抛物线的两切线，设两切点分别为、，记线段的中点为．
(1)证明：线段的中点在抛物线上；
(2)设点为圆上的点，当取最大值时，求点的纵坐标．
【答案】(1)证明见解析；(2).
【解析】(1)设直线的方程为，
联立，可得，
，，
所以，直线的方程为，即，
同可知直线的方程为.
联立，解得，即点，
线段的中点为，
所以，线段的中点为，
因此，，因此，线段的中点在抛物线上；
(2)由(1)知，，
，
，
令，则，
所以，，
所以，当时，即当时，取最大值，
此时，解得，
因此，当取最大值时，点的纵坐标为.
7．(2024·深州长江中学)已知直线：与轴交于点，且，其中为坐标原点，为抛物线：的焦点.
(1)求拋物线的方程；
(2)若直线与抛物线相交于，两点(在第一象限)，直线，分别与抛物线相交于，两点(在的两侧)，与轴交于，两点，且为中点，设直线，的斜率分别为，，求证：为定值；
(3)在(2)的条件下，求的面积的取值范围.
【答案】(1)；(2)证明见解析；(3).
【解析】(1)由已知得，且为的中点，所以 .
所以，解得，
故抛物线的方程为.
(2)证明：联立，解得 ，，
由为的中点得.
不妨设，，其中 .
则，.
所以，
即为定值.
(3)由(2)可知直线的方程为，即 ，
与抛物线联立，消 x可得，
解得或(舍)，
所以，即 ，
故点到直线的距离.
设过点的抛物线的切线方程为，
联立得 ，
由，得，
所以切线方程为，令，得 ，
所以要使过点的直线与抛物线有两个交点，，
则有，
又，
所以，
即，故 的面积的取值范围为.
8(2024·浙江高三其他模拟)已知椭圆：的左、右焦点分别是，，且经过点，直线与轴的交点为，的周长为．
(1)求椭圆的标准方程；
(2)若是坐标原点，，两点(异于点)是椭圆上的动点，且直线与直线的斜率满足，求面积的最大值．
【答案】(1)；(2)．
【解析】(1)∵的周长为，
∴，∴．
将代入，得，解得．
∴椭圆的标准方程是．
(2)由题意知直线的斜率存在且不为0，
设直线的方程为，，，
将与联立并消去，整得，
则，．
∵，
∴，
∴，
化简得，
∴或(舍去)．
当时，，则，得．
，
原点到直线的距离，
∴，
当且仅当，即时取等号，经验证，满足题意．
∴面积的最大值是．
9．(2024·全国高三月考())如图，已知椭圆的右焦点为，原点为，椭圆的动弦过焦点且不垂直于坐标轴，弦的中点为，椭圆在点处的两切线的交点为.
(1)求证：三点共线；
(2)求的最小值.
【答案】(1)证明见解析；(2).
【解析】(1)椭圆的右焦点为，
设所在的直线的方程为，且
联立方程组可得：
则，，点的坐标为，
所在的直线的方程为，
设在点处的切线为：，与椭圆联立后由，可得，整得：椭圆在处的切线方程为，，
联立方程组，
解得点的坐标为，
，
故三点共线.
(2)由(1)可知，
，
当且仅当即时，等号成立.
10．(2024·浙江高三其他模拟)设为坐标原点，是轴上一点，过点的直线交抛物线：于点，，且．
(1)求点的坐标；
(2)求的最大值．
【答案】(1)；(2)2．
【解析】(1)设，，，
则，解得，
设直线，联立方程，得得，
由根与系数的关系知，，所以，
故点的坐标为．
(2)由(1)知，，．
易知，，
所以，
则．
令，，则，
所以在上单调递增，在上单调递减，
所以，即的最大值是2，当且仅当时取
备战高考数学成套的一轮复习，二轮复习，专题高分突破，考前回归，模拟试卷尽在备战高考QQ群722859698也可联系微信fjshuxue加入夸克网盘群3T一线老师必备资料一键转存自动更新永不过期