中考数学一轮复习过关练4.5 相似三角形重难点题型讲练（讲练）（2份，原卷版+解析版）

这是一份中考数学一轮复习过关练4.5 相似三角形重难点题型讲练（讲练）（2份，原卷版+解析版），文件包含中考数学一轮复习过关练45相似三角形重难点题型讲练讲练原卷版doc、中考数学一轮复习过关练45相似三角形重难点题型讲练讲练解析版doc等2份试卷配套教学资源，其中试卷共192页， 欢迎下载使用。
类型1-相似多边形的判定
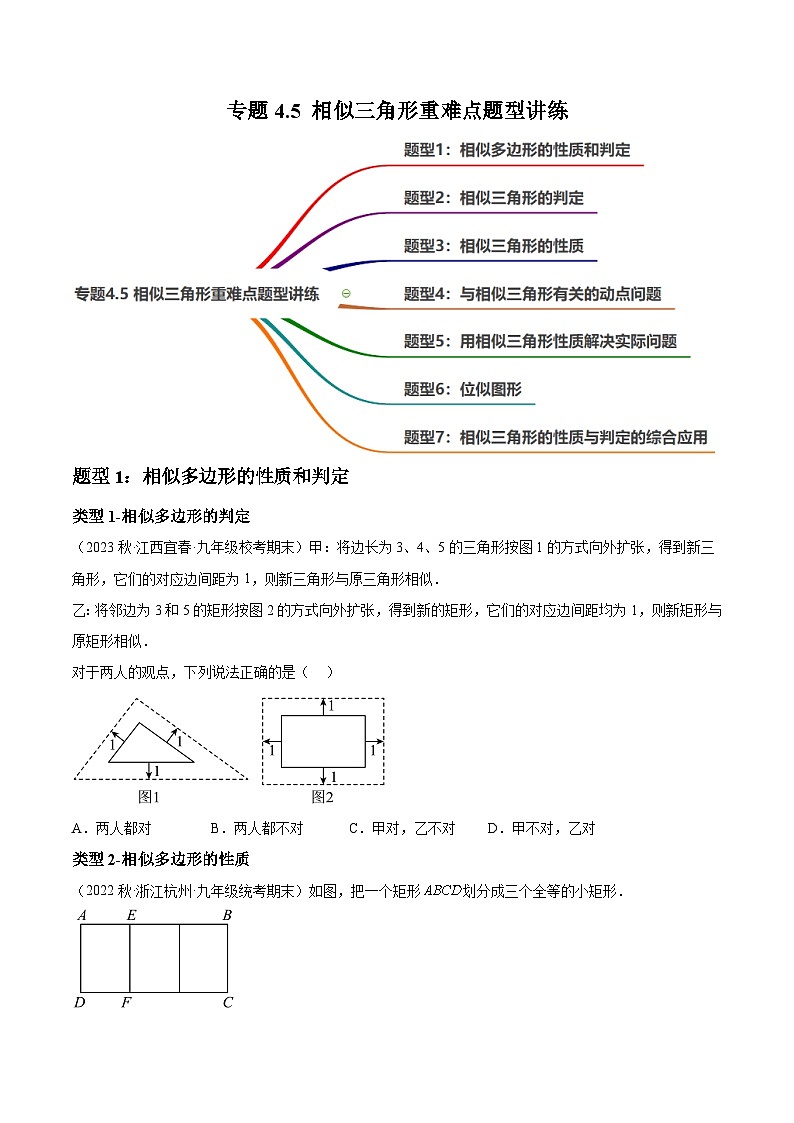
（2023秋·江西宜春·九年级校考期末）甲：将边长为3、4、5的三角形按图1的方式向外扩张，得到新三角形，它们的对应边间距为1，则新三角形与原三角形相似．
乙：将邻边为3和5的矩形按图2的方式向外扩张，得到新的矩形，它们的对应边间距均为1，则新矩形与原矩形相似．
对于两人的观点，下列说法正确的是（ ）
A．两人都对B．两人都不对C．甲对，乙不对D．甲不对，乙对
类型2-相似多边形的性质
（2022秋·浙江杭州·九年级统考期末）如图，把一个矩形划分成三个全等的小矩形．
(1)若原矩形的长，宽．问：每个小矩形与原矩形相似吗？请说明理由．
(2)若原矩形的长，宽，且每个小矩形与原矩形相似，求矩形长与宽应满足的关系式．
综合训练
1．（2022秋·河北邢台·九年级校考阶段练习）甲说：“将三角形各边向内平移1个单位长度并适当缩短，得到如图1所示的图形，变化前后的两个三角形相似．”
乙说：“将菱形各边向内平移1个单位长度并适当缩短，得到如图2所示的图形，变化前后的两个菱形相似．”
对于两人的观点，下列说法正确的是（ ）
A．两人都对B．两人都不对C．甲对，乙不对D．甲不对，乙对
2．（2023秋·辽宁沈阳·九年级统考期末）如图，有三个矩形，其中是相似图形的是（ ）
A．甲和乙B．甲和丙C．乙和丙D．甲、乙和丙
3．（2023秋·浙江绍兴·九年级统考期末）两个大小不一的五边形和五边形如图所示放置，点F在线段上，点H在线段上，对应连接并延长刚好交于一点O，则这两个五边形的关系是（ ）
A．一定相似B．一定不相似C．不一定相似D．不能确定
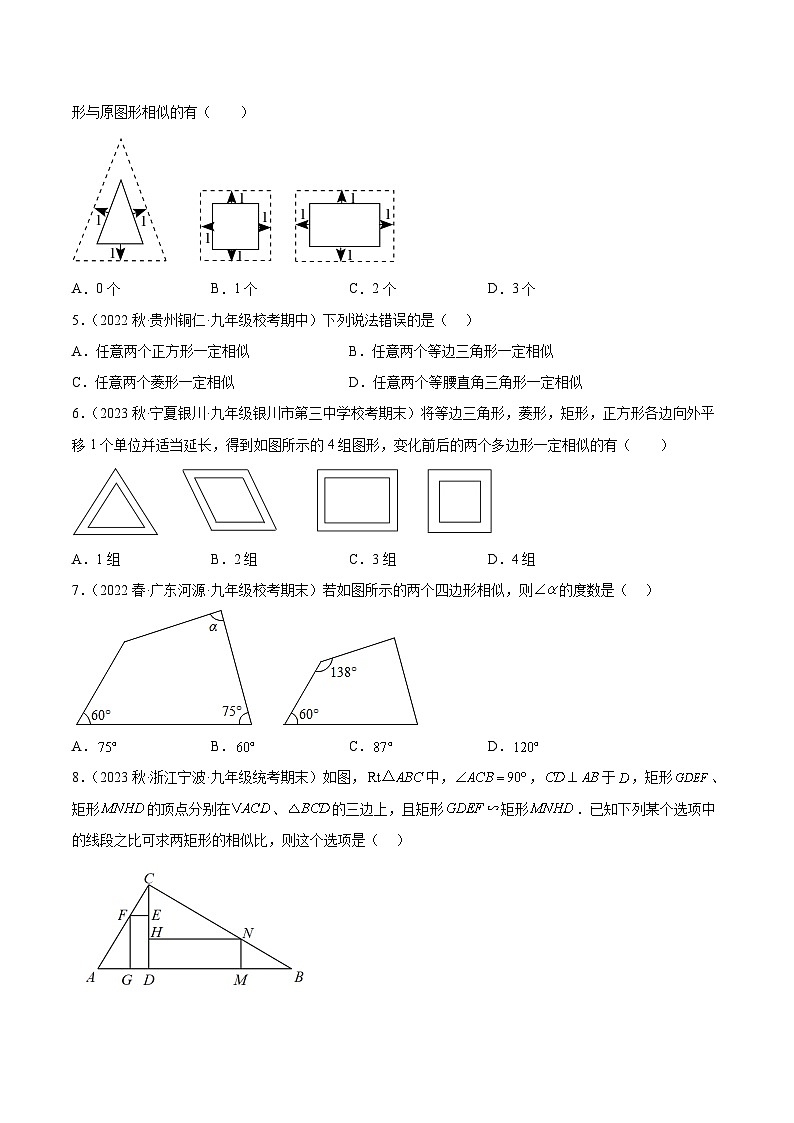
4．（2023秋·河北张家口·九年级校考阶段练习）将边长为4，6，6的等腰三角形、边长为4的正方形和长、宽分别为6，4的矩形按如图所示的方式向外扩张，各得到一个新图形，它们的对应边间距均为1，则新图形与原图形相似的有（ ）
A．0个B．1个C．2个D．3个
5．（2022秋·贵州铜仁·九年级校考期中）下列说法错误的是（ ）
A．任意两个正方形一定相似B．任意两个等边三角形一定相似
C．任意两个菱形一定相似D．任意两个等腰直角三角形一定相似
6．（2023秋·宁夏银川·九年级银川市第三中学校考期末）将等边三角形，菱形，矩形，正方形各边向外平移1个单位并适当延长，得到如图所示的4组图形，变化前后的两个多边形一定相似的有（ ）
A．1组B．2组C．3组D．4组
7．（2022春·广东河源·九年级校考期末）若如图所示的两个四边形相似，则的度数是（ ）
A．B．C．D．
8．（2023秋·浙江宁波·九年级统考期末）如图，中，，于，矩形、矩形的顶点分别在、的三边上，且矩形矩形．已知下列某个选项中的线段之比可求两矩形的相似比，则这个选项是（ ）
A．B．C．D．
9．（2023秋·浙江宁波·九年级统考期末）一个大矩形按如图方式分割成五个小矩形后仍是中心对称图形，且矩形矩形．设矩形与矩形的面积分别为m和n，则这个大矩形的面积一定可以表示为（ ）
A．B．C．D．
10．（2023秋·浙江宁波·九年级统考期末）如图，在平行四边形中，点分别在边上，，四边形四边形，相似比，则下列一定能求出面积的条件（ ）

A．四边形和四边形的面积之差B．四边形和四边形的面积之差
C．四边形和四边形的面积之差D．四边形和四边形的面积之差
11．（2022秋·浙江·九年级专题练习）如图，梯形中，E、F分别为、两腰上的点，且．若，，且梯形与梯形相似，则与的比值为（ ）
A．B．C．D．
12．（2023·河北衡水·校考二模）将边长为2的正六边形按照如图所示的方式向外扩张，得到新的六边形，它们的对应边的距离均为．
（1）新的六边形与原六边形_____；（填“相似”或“不相似”）
（2）扩张后六边形的周长比原来增加了______．
13．（2022秋·浙江宁波·九年级浙江省余姚市实验学校校考期末）如图，矩形中，，剪去一个矩形后，余下的矩形矩形，则的长为___________．
14．（2022秋·浙江·九年级专题练习）矩形纸片的边长为，动直线l分别交于E、F两点，且∶
(1)若直线l是矩形的对称轴，且沿着直线l剪开后得的矩形与原矩形相似，试求的长？
(2)若使，试探究：在边上是否存在点E，使剪刀沿着直线l剪开后，所得到的小矩形纸片中存在与原矩形相似的情况．若存在，请求出的值，并判断E点在边上位置的特殊性；若不存在，试说明理由．
15．（2023·陕西西安·校考一模）如图1，矩形的一边落在矩形的一边上，并且矩形矩形，其相似比为，矩形的边，．
(1)矩形的面积是 ；
(2)将图1中的矩形绕点逆时针旋转90°，若旋转过程中与夹角（图2中的）的正切的值为，两个矩形重叠部分的面积为，求与的函数关系式；
(3)将图1中的矩形绕点逆时针旋转一周，连接、，的面积是否存在最大值或最小值？若存在，求出最大值或最小值；若不存在，请说明理由．
题型2：相似三角形的判定
类型1 添加条件证明三角形相似
（2023秋·江苏宿迁·九年级统考期末）如图，要使，还需要添加一个条件，你添加的条件是____________（只写一种情况即可）．
类型2证明三角形相似
（2022秋·陕西渭南·九年级统考期末）如图，点为边上一点，连接，，，．
求证：．
类型3网格图中的三角形相似
（2022秋·浙江杭州·九年级杭州市十三中教育集团（总校）校联考期末）如图，的顶点均为网格中的格点．
(1)选择合适的格点（包括边界）为点D和点E，请画出一个，使（相似比不为1）．
(2)证明：．
综合训练
1．（2023·全国·九年级专题练习）如图，已知，那么添加下列一个条件后，仍然无法判定的是（ ）
A．B．C．D．
2．（2023春·安徽蚌埠·九年级校考阶段练习）如图，在和中，，要使与相似，还需要添加一个条件，这个条件是（ ）
A．B．C．D．
3．（2023·河北秦皇岛·统考一模）如图，在中，，点D为线段上一动点（不与点B，C重合），连接，作，交线段于点E．
下面是某学习小组根据题意得到的结论：
甲同学：；
乙同学：若，则；
丙同学：当时，D为的中点．
则下列说法正确的是（ ）
A．只有甲同学正确B．乙和丙同学都正确
C．甲和丙同学正确D．三个同学都正确
4．（2022秋·贵州贵阳·九年级统考期末）如图，在中，，，，将沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（ ）
A．B．
C．D．
5．（2022秋·福建宁德·九年级统考阶段练习）如图，点P是的边上一点，连接，以下条件中，不能判定的是（）
A．B．
C．D．
6．（2022秋·黑龙江齐齐哈尔·九年级统考期末）如图，、分别是、上两点，与相交于点，下列条件中不能使和相似的是（ ）
A．B．
C．，D．
7．（2023秋·河北保定·九年级校考期末）如图，在中，．将沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（ ）
A．B．
C．D．
8．（2023秋·广西贺州·九年级统考期末）如图，在四边形中，与相交于点O，则下列三角形中，与一定相似的是（ ）
A．B．C．D．
9．（2023秋·四川乐山·九年级统考期末）如图，在中，是斜边上的高，于点．除自身外，图中与相似的三角形的个数是___________．
10．（2022·广东汕头·一模）如图所示，在正方形中，是上的点，且，是的中点．
(1)与是否相似？为什么？
(2)试问：与有什么关系？
11．（2023·江苏宿迁·统考一模）如图，是的内接三角形，点D是的中点，弦交于点E．与相似吗？为什么？
12．（2023秋·广东河源·九年级校考期末）如图，，与交于点E.
(1)
(2)若，，，求的长；
13．（2022秋·江苏无锡·九年级统考期末）如图，已知，，且，将边反向延长至点D，使，连接．
(1)求证：；
(2)求的长．
14．（2023秋·福建泉州·九年级统考期末）如图，四边形ABCD中，，，．
(1)尺规作图：在上求作一点E，使得；（保留作图的迹，不写作去）
(2)在（1）的条件下，连接DE．求证：．
15. （2023秋·江苏徐州·九年级统考期末）如图，在中，C、D为边上的两个动点，．

(1)若，则与相似吗?为什么?
(2)若（即C、D重合），则_______°时，；
(3)当和满足怎样的数量关系时，?请说明理由．
题型3：相似三角形的性质
（2022秋·陕西西安·九年级统考期中）如图，在平面直角坐标系中，已知，点A的坐标为，点B的坐标为．若a，b的值是关于x的一元二次方程的两个根，且．
(1)直接写出___________，___________
(2)若点P在y轴上，且，求点P的坐标．
综合训练
1．（2022·辽宁营口·一模）如图，将等边三角形沿边上的高线平移到，阴影部分面积记为，若， ，则_____．
2．（2023春·辽宁本溪·九年级统考开学考试）如图，点，，点是第一象限内一动点，且，若与相似，则的长为______．
3．（2023·全国·九年级专题练习）如图，在中，点为边的中点，点为上一点，且，连接并延长交的延长线于点．求证：．
4．（2022秋·江苏无锡·九年级统考期末）如图，是的内接三角形，是的中点，交于点．
(1)求证：；
(2)若，，求的长．
5．（2023秋·河北秦皇岛·九年级统考期末）如图1，为等边三角形，，点D为边上的动点（点D不与点B，C重合），且，交边于点E．
(1)求证：；
(2)如图2，当D运动到的中点时，求线段的值；
6．（2023·安徽淮北·校联考一模）如图，四边形中，对角线，相交于点，且，．
(1)若，求证：；
(2)求证：；
(3)若平分，，，求的长．
题型4：与相似三角形有关的动点问题
类型1-双动点问题
（2023·山东青岛·统考一模）如图，在矩形中，，，动点P从点D出发沿向终点A运动，同时动点Q从点A出发沿对角线向终点C运动．过点P作，交于点E，动点P、Q的运动速度是每秒1个单位长度，当点P运动到点A时，P、Q两点同时停止运动．设运动时间为，解答下列问题：
(1)当E、Q重合时，求t的值；
(2)设四边形的面积为S，当线段在点Q右侧时，求出S与t之间的函数关系式；
(3)当时，求t的值；
(4)是否存在这样的点P和点Q，使P、Q、E为顶点的三角形是等腰三角形？若存在，请求出所有满足要求的t的值；若不存在，请说明理由．
类型2-动图问题
（2023秋·四川乐山·九年级统考期末）如图，正方形的边与矩形的边重合，将正方形以秒的速度沿方向移动，移动开始前点与点重合．已知正方形的边长为，，，设正方形移动的时间为秒，且．
(1)当______秒时，；
(2)若以、、为顶点的三角形同相似，求的值；
(3)过点作交于点，连接．
①若的面积为，的面积为，则的值会发生变化吗？请说明理由；
②当线段所在直线与正方形的对角线垂直时，求线段的长．
综合训练
1．（2023·安徽合肥·合肥一六八中学校考模拟预测）如图，中，，，．点P从点C出发沿折线CA-AB以每秒1个单位长的速度向点B匀速运动，点1从点B出发沿BC-CA-AB以每秒2个单位长的速度向点B匀速运动，点P，Q同时出发，当其中一点到达点B时停止运动，另一点也随之停止．设点P，Q运动的时间是t秒（）．
发现：
(1)___________；
(2)当点P，Q相遇时，相遇点在哪条边上？并求出此时AP的长．
探究：
(3)当时，的面积为___________；
(4)点P，Q分别在AC，BC上时，的面积能否是面积的一半？若能，求出t的值；若不能，请说明理由．
拓展：
(5)当时，求出此时t的值．
2．（2023秋·辽宁沈阳·九年级统考期末）如图，在平面直角坐标系中，O是坐标原点，矩形的两边分别在x轴和y轴上，点B的坐标为，现有两动点P，Q，点P以每秒3个单位的速度从点O出发向终点A运动，同时点Q以每秒2个单位的速度从点A出发向终点B运动，连接，，．设运动时间为t秒（）．
(1)点P的坐标为______，点Q的坐标为______（用含t的代数式表示）；
(2)请判断四边形的面积是否会随时间t的变化而变化，并说明理由；
(3)若以A，P，Q为顶点的三角形与相似时，请直接写出t的值．
3．（2022·河北保定·保定十三中校考二模）如图，中，，，．动点从点出发，以每秒3个单位长度的速度沿方向绕行一周，与垂直的动直线从开始．以每秒1个单位长度的速度向右平移，分别交，于，两点．当点运动到点时，直线也停止运动，设点的运动时间为秒．
(1)当点P在上运动时，过点作于F，
①当时，求证：；
②设的面积为S，用含t的代数式表示S，并求当t为何值时，S有最大值；
(2)当直线l等分的面积时求t的值，并判断此时点P落在的哪条边上；
(3)直接写出时t的值．
4．（2023·全国·九年级专题练习）如图1，，，，点从点出发以每秒1个单位长度的速度向点运动，点同时从点出发以每秒2个单位长度的速度向点A运动，当一点到达终点时，另一点也停止运动．
(1)求的长．
(2)当以点、、为顶点的三角形与相似时，求的值．
(3)如图2，将本题改为点从点出发以每秒3个单位长度的速度在上向点运动，点同时从点出发向点运动，其速度是每秒2个单位长度，其它条件不变，求当为何值时，为等腰三角形．
5．（2023秋·浙江金华·九年级统考期末）如图1，在矩形中，，，动点P从点A出发，沿边以每秒2个单位的速度向点B运动，同时，动点Q从点B出发，沿匀速向终点D运动，点P、Q同时到达终点，与交于点E．过点B作于点F．设点P、Q的运动时间为t秒．
(1)求点Q的运动速度．
(2)如图2，当点Q与点C重合时，求的长．
(3)在点P、Q的运动过程中，是否存在某一时刻，使得以B、E、F为顶点的三角形与相似？若存在，求运动时间t的值；若不存在，请说明理由．
6．（2022秋·安徽滁州·九年级校考阶段练习）如图1，在中，，，点P、Q分别在射线、上（点P不与C，B重合），且保持．
(1)若P在线段上，求证：；
(2)设、，求y与x之间的函数关系式，并写出x的取值范围；
(3)如图2，正方形的边长为4，点P、Q分别在直线、上（点P不与C，B重合），且保持，当时，直接写出的长．
7．（2022·广东东莞·东莞市横沥中学统考一模）如图甲，在中．．．．如果点由点出发沿方向向点匀速运动．同时点由点出发沿方向向点匀速运动．它们的速度均为每秒钟1个单位长度．连接，设运动时间为秒钟．
(1)设的面积为，当实数为何值时，取得最大值？的最大值是多少？
(2)在（1）的前提下．当取得最大值时．把此时的沿射线以每秒钟1个单位长度的速度平移，当点平移至与点重合时停止，写出平移过程中，与的重叠部分面积与平移时间的函数解析式，并写出对应的的取值范围；
(3)如图乙，连接，将沿翻折，得到四边形，当四边形为菱形时，求实数的值．
8．（2022秋·陕西西安·九年级校考期中）综合与探究：已知：如图①，在中，，，，点由出发沿方向向点匀速运动，速度为；点由出发沿方向向点匀速运动，速度为；连接．若设运动的时间为，解答下列问题：
(1)当时，求的值；
(2)点，同时出发，为何值时，以，，为顶点的三角形与相似；
(3)如图②，连接，并把沿翻折，得到四边形，那么是否存在某一时刻，使四边形为菱形？若存在，直接写出此时的值；若不存在，说明理由，（不写求解过程）
9．（2022秋·河北邯郸·九年级邯郸市第二十三中学校考期末）如图（1），在四边形中，，，，，动点从点开始沿边匀速运动，动点从点开始沿边匀速运动，它们的运动速度均为．点和点同时出发，设运动的时间为，．
(1)用含的代数式表示；
(2)当以点、、为顶点的三角形与相似时，求的值；
(3)如图（2），延长、，两延长线相交于点，当为直角三角形时，直接写出的值．
题型5：用相似三角形性质解决实际问题
（2023秋·河北邯郸·九年级校考期末）某数学兴趣小组的名同学利用课余时间想要测量学校里两棵树的高度，在同一时刻的阳光下，他们合作完成了以下工作：
(1)测得一根长为米的竹竿的影长为米，甲树的影长为米（如图1）．
(2)测量的乙树的影子除落在地面上外，还有一部分落在教学楼的第一级台阶上（如图2），测得落在地面上的影长为米，一级台阶高为米，落在第一级台阶的影子长为米，
①甲树的高度为______米，
②图3为图2的示意图，请利用图3求出乙树的高度．
综合训练
1．（2023·河北秦皇岛·模拟预测）九章算术记载“今有邑方不知大小，各中开门．出北门三十步有木，出西门七百五十步见木．问邑方有几何？”意思是：如图，点、点分别是正方形的边、的中点，，，过点，且步，步，则正方形的边长为( )
A．步B．步C．步D．步
2．（2023春·辽宁本溪·九年级统考开学考试）《海岛算经》是我国最早的一部测量数学专著，书中第一个问题的大意是：如图，要测量海岛上一座山峰的高度，立两根长度相等的标杆和，两杆之间的距离步，，，共线；从到走123步，此时A，，三点共线；从到走127步，此时A，，三点共线．计算山峰的高度及的长．若设步，所列方程正确的是（ ）
A．B．
C．D．
3．（2023秋·黑龙江哈尔滨·九年级统考期末）如图，某零件的外径为，用一个交叉卡钳（两条尺长和相等）可测量零件的内孔直径．如果，且量得，则零件的厚度x为（ ）
A．B．C．D．
4．（2023·广东佛山·统考一模）如图，周一某校升国旗时，甲、乙两名同学分别站在、的位置时，乙的影子刚好在甲的影子里边，已知甲身高为米，乙身高为米，甲的影长是6米，则甲、乙同学相距______米．
5．（2023秋·湖北随州·九年级统考期末）如图，小明同学用自制的直角三角形纸板测量树的高度，他调整自己的位置，设法使斜边保持水平，并且边与点在同一直线上．已知纸板的两条直角边，，测得边离地面的高度，，则树高为______．
6．（2023秋·辽宁沈阳·九年级统考期末）如图，数学实践课上，老师布置任务如下：让小明站在B点处去观测外的位于D点处的一棵大树，所用工具为一个平面镜P和必要的长度测量工具（点B，P，D在同一条直线上）．已知小明眼睛距地面，大树高，当小明与平面镜相距______m时，恰好能从平面镜里观测到大树的顶端．
7．（2023秋·江苏南通·九年级统考期末）《海岛算经》中记载：“今有望海岛，立两表齐高三丈，前后相去千步，令后表与前表参相直，从前表却行一百二十三步，人目着地，取望岛峰，与表末参合．从后表却行一百二十七步，人目着地，取望岛峰，亦与表末参合．问岛高几何．”其大意是：如图，为了求海岛上的山峰的高度，在处和处树立高都是3丈丈步）的标杆和，，相隔1000步，并且，和在同一平面内，从处后退123步到处时，，，在一条直线上；从处后退127步到处时，，，在一条直线上，则山峰的高度为 _____步．
8．（2023春·江苏南通·九年级南通田家炳中学校考开学考试）如图，为驾驶员的盲区，驾驶员的眼睛点P处与地面的距离为米，且满足，若盲区的长度是6米，则车宽的长度为______米．
9．（2022秋·浙江湖州·九年级统考期末）如图1是一个家用折叠梯子，使用时四个踏板都是平行于地面且全等的矩形，已知踏板宽，，将踏板往上收起时（如图2），点A与点F重合，此时，踏板可以看作与支架重合，将梯子垂直摆放时，点A离地面的高度为____________．图3是图1的简略视图，若点H恰好在点A的正下方，此时点A到地面的高度是____________．
10．（2023·陕西西安·西北大学附中校考三模）小延想要测量学校教学楼的高度，他站在N点处时，视线通过旗杆的顶端与顶楼的窗子下沿C重合，他向前走到点G处时，视线通过旗杆的顶端与楼顶A重合，已知小延的眼睛与地面的距离米，米，米，米，米，、、、均与地面垂直，且在同一平面内，请你根据以上数据计算教学楼的高度．
11．（2023·陕西宝鸡·统考一模）小明和小华利用学过的知识测量操场旗杆的高度，测量时，小明让小华站在点B处，此时，小华影子的顶端E与旗杆的影子C顶端重合，且的长为2米；小明又让小华沿着射线的方向走15.2米到达旗杆的另一侧N处，此时，小华观测到旗杆顶端C的仰角为，已知小华的身高为1.8米，请你根据相关测量信息，计算旗杆的高度．
12．（2023春·广东揭阳·九年级普宁二中实验学校校考阶段练习）小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高，如图所示，在某一时刻，他们在阳光下，分别测得该建筑物的影长为米，的影长为米，小明的影长为米，其中、、、、五点在同一直线上，、、三点在同一直线上，且，，已知小明的身高为米，求旗杆的高．
13．（2023·陕西西安·统考一模）某数学兴趣小组决定利用所学知识测量一古建筑的高度．如图2，古建筑的高度为，在地面上取E，G两点，分别竖立两根高为的标杆和，两标杆间隔为，并且古建筑，标杆和在同一竖直平面内．从标杆后退到D处（即），从D处观察A点，A、F、D三点成一线；从标杆后退到C处（即），从C处观察A点，A、H、C三点也成一线．已知B、E、D、G、C在同一直线上，，，，请你根据以上测量数据，帮助兴趣小组求出该古建筑的高度．
14．（2023秋·江苏南京·九年级统考期末）如图，道路l的正上方挂有一盏路灯M，把路灯M看成一个点光源，路灯M到道路l的距离为，晚上，一名身高为的小女孩沿着道路l散步，从A处径直向前走到达C处．已知小女孩在A处影子的长为，在C处影子的长为，求小女孩的身高．
15．（2023秋·河北唐山·九年级校考期末）某校九年级一班的一节数学活动课安排了测量操场上竖直的悬挂国旗的旗杆的高度．甲、乙、丙三个学习小组设计的测量方案如图所示：甲组测得图中米，米，米；乙组测得图中，米，同一时刻影长米，米；丙组测得图中，，，米，米，人的臂长为0.6米，请你任选两种方案，利用实验数据求出该校旗杆的高度．
题型6：位似图形
类型1 与图形位似有关的计算
（2023秋·四川眉山·九年级统考期末）如图，与位似，点为位似中心，已知，的面积为2，则的面积为______．
类型2 位似图形的作图
（2022秋·山东济宁·九年级统考期末）如图所示，在网格中，每个小正方形的边长均为1个单位长度，把小正方形的顶点叫做格点，为平面直角坐标系的原点，矩形的4个顶点均在格点上，连接对角线．
(1)在平面直角坐标系内，以原点为位似中心，把缩小，作出它的位似图形，并且使所作的位似图形与的相似比等于；
(2)在（1）的条件下，若是边上任意一点，则变换后点P的对应点的坐标为 ．
例10.（2023·四川宜宾·校考模拟预测）如图，在正方形中，点E是上的一点，点F是延长线上的一点，且，连接、、．
(1)求证；
(2)若，请求出的长．
综合训练
1．（2023春·重庆九龙坡·九年级重庆实验外国语学校校考阶段练习）如图，平面直角坐标系中，与关于原点位似，，若四边形的面积为4，则四边形的面积为（ ）
2．（2022春·黑龙江大庆·八年级大庆市第六十九中学校考期中）如图，在中，三个顶点的坐标分别是，，．以点C为位似中心，在x轴下方作的位似图形，并把的边长放大为原来的2倍，那么点的坐标为_______．
3．（2023秋·海南海口·九年级校联考期末）如图，在平面直角坐标系中，的顶点坐标分别为、、，是的边上一点．
(1)以原点O为位似中心，在y轴的右侧画出的一个位似，使它与的相似比为，并分别写出点、的对应点、的坐标；
(2)画出将向左平移2个单位，再向上平移1个单位后的，并写出点、的对应点、的坐标；
(3)判断与，能否是关于某一点为位似中心的位似图形，若是，请在图中标出位似中心，并写出点的坐标．
4．（2023秋·江苏南通·九年级统考期末）如图，在平面直角坐标系中，，O，A，C三点在同一直线上，，则点C的坐标为（ ）
A．B．C．D．
5．（2023·四川宜宾·校考模拟预测）如图，和是以点为位似中心的位似图形，点的坐标为，若点、、的坐标分别是、、．则点的对应点的坐标是（ ）
6．（2023春·湖南长沙·九年级校考阶段练习）如图，在平面直角坐标系中，已知点，，以原点为位似中心，将扩大为原来的4倍，则点A的对应点的坐标是（ ）
A．B．
C．或D．或
7．（2022秋·四川成都·九年级统考期末）在平面直角坐标系中，已知点，，以原点为位似中心，相似比为，把缩小，则点的对应点的坐标是（ ）
A．B．C．或D．或
8．（2023秋·贵州六盘水·九年级统考期末）如图，在平面直角坐标系中，与是位似图形，且顶点都在格点上，则位似中心的坐标是（ ）
A．B．C．D．
9．（2022秋·重庆北碚·九年级西南大学附中校考开学考试）在平面直角坐标系中，点，，以原点为位似中心，相似比为，把缩小，则点的对应点的坐标是（ ）
A．B．C．或D．或
10．（2023春·安徽安庆·九年级校联考阶段练习）如图，平面直角坐标系中点是的边上的任意一点．
(1)以点为位似中心，在M点的右侧把△按放大得，画出；直接写出的边上与点的对应点的坐标．
(2)将绕逆时针转90º得，画出，求旋转过程中线段在平面上扫过部分的面积（用表示）
11．（2023秋·河南平顶山·九年级统考期末）如图，在平面直角坐标系中，已知与位似，的顶点坐标分别是，，，的顶点坐标分别是，，．
(1)若位似中心为，请写出点的坐标为______；
(2)以点为位似中心，作的位似图形，使与的相似比为．请在图中画出符合要求的的图像并写出的坐标．
12．（2023·安徽合肥·校考一模）在平面直角坐标系xOy中的位置如图所示．
(1)作关于点C成中心对称的；
(2)以为位似中心，在图中画出将面积放大4倍后的，计算的面积并直接写出点的坐标．
13．（2022秋·安徽蚌埠·九年级校考期末）如图，在平面直角坐标系中，的三个顶点坐标分别为，，．
(1)以原点O为位似中心，位似比为，在第二象限画出放大后的图形，点A，B，C的对应点分别为点，，，并直接写出点的坐标；
(2)点是线段BC上的一点，请直接写出点D经过（1）的变化后对应点的坐标．
14．（2023·四川成都·统考一模）如图，在平面直角坐标系中，的顶点坐标分别为，，（每个方格的边长均为1个单位长度）．
(1)将先向左平移4个单位，再向上平移1个单位后得到，请在平面直角坐标系中画出平移后的．
(2)请以O为位似中心，在y轴右侧画出的位似图形，使与的相似比为，则点的坐标为（__________，__________）；点的坐标为（__________，__________）．
15．（2023秋·吉林长春·九年级统考期末）图①、图②均是的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点，的顶点均在格点上，只用无刻度的直尺，在给定的网格中，分别按下列要求画图，保留适当的作图痕迹，不要求写出画法．
(1)在图①中的线段上找一点D，线段上找一点E，连接，使是的中位线，并直接写出线段的长．
(2)在图②中，以点A为位似中心，作的位似，使与的面积比为．
题型7：相似三角形的性质与判定的综合应用
（2022秋·浙江·九年级期末）在中，，点D在直线上，连结，以为边作等腰直角（点E在直线右侧），连结．
（1）如图1，若，且点D在边上，求证：；
（2）如图2，若，且，，求的长；
（3）如图3，若点D在的延长线上，，相交于点F，设的面积为，的面积为，的面积为，则，请说明理由．
综合训练
1．（2023春·黑龙江哈尔滨·九年级哈尔滨市虹桥初级中学校校考阶段练习）如图1，已知：内接于圆O，，连接并延长，交于点D．
(1)求证：
(2)如图2，过点B作于点E，交圆O于点F，交于点G，求证：；
(3)如图3，在（2）的条件下，连接DE，，，求DE的长．
2．（2023秋·河北承德·九年级统考期末）如图，某水果的横断面是以为直径的半圆，其中水面截线，嘉琪在处测得垂直站立于处的爸爸头顶的仰角为，点的俯角行为，已知爸爸的身高为1.7m
(1)求大小及的长；
(2)图中线段表示最大水深，并求最大水深约为多少米（结果保留小数点后一位）．（参考数据：取4，取4.1）
3．（2022秋·福建泉州·九年级校考阶段练习）【基础探究】（1）如图①，在中，为上一点，，交延长线于点，若，求的长．
【拓展延伸】（2）如图②，在中，为上一点，，交延长线于点，，， ，则 ．
【拓展延伸】（3）如图③，点为四边形内部一点，且有，，于点，为上一点，，若，，则的面积为 ．
4．（2022·安徽·九年级专题练习）如图，在中，，为上一点，经过点的分别交，于点，，与相切于点，连接，相交于点．
(1)求证：平分；
(2)求证：；
(3)若，，求的长．
5．（2022·重庆·模拟预测）在等腰直角中，，，外有一点D满足，BD与AC相交于点E，连接CD．
(1)如图1，若，，求BD的长；
(2)如图2，点F为BD上一点，连接CF，点G为CF的中点，连接DG，若，猜想BF与CD存在的数量关系，并证明你的猜想；
(3)如图3，在（2）问条件下，当F为BD的中点时，将沿直线AB翻折至所在平面内，得，连接、，AG，请直接写出的比值．
6．（2022春·全国·九年级期末）如图，四边形ABCD是矩形．
(1)如图1，E、F分别是AD、CD上的点，BF⊥CE，垂足为G，连接AG．
①求证：＝．
②若G为CE的中点，求证：sin∠AGB＝；
(2)如图2，将矩形ABCD沿MN折叠，点A落在点R处，点B落在CD边的点S处，连接BS交MN于点P，Q是RS的中点．若AB=2，BC=3，求PS+PQ的最小值．
7．（2021秋·福建漳州·九年级福建省诏安第一中学校考期中）如图，已知正方形ABCD，点E为AB上的一点，，交BD于点F．
(1)如图1，直按写出的值_______；
(2)将△EBF绕点B顺时针旋转到如图2所示的位置，连接AE、DF，猜想DF与AE的数量关系，并证明你的结论；
(3)如图3，当BE=BA时，其他条件不变，△EBF绕点B顺时针旋转，设旋转角为，当为何值时EA=ED?请在图3或备用图中画出图形并求出的值．
8．（2022春·全国·九年级期末）如图，⊙O是△ABC的外接圆，AB为直径，弦AD平分∠BAC，过点D作射线AC的垂线，垂足为M，点E为线段AB上的动点．
(1)求证：MD是⊙O的切线；
(2)若∠B＝30°，AB＝8，在点E运动过程中，EC+EM是否存在最小值？若存在，请求出最小值；若不存在，说明理由；
(3)若点E恰好运动到∠ACB的角平分线上，连接CE并延长，交⊙O于点F，交AD于点P，连接AF，CP＝3，EF＝4，求AF的长．
9．（2022秋·湖南永州·九年级统考期中）如图，在梯形中，，，，点、分别在线段、上，．的延长线交边于点，交于点、其延长线交的延长线于点．
（1）求证：；
（2）设，的面积为，求关于的函数解析式，并写出它的定义域；
（3）联结，当与相似时，求的长．
10．（2021·安徽·九年级专题练习）如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E处，过点E作EG∥CD交AF于点G，连接DG．
（1）求证：四边形EFDG是菱形；
（2）求证EG2＝GF•AF；
（3）若AG＝3，EG＝，求BE的长．
11．（2022秋·江苏泰州·九年级靖江市靖城中学校联考阶段练习）在矩形ABCD的CD边上取一点E，将沿BE翻折至的位置．
（1）如图1，当点F落在矩形ABCD内部时，连接CF并延长，交AD于点G，若，，，则GF的长度为________________；
（2）如图2，当点C恰好落在AD边上点F处时，若，且，求BC的长；
（3）如图3，当点C恰好落在AD边上点F处时，延长EF，与的角平分线交于点M，BM交AD于点N，当时，求的值．
12．（2021春·江苏苏州·八年级统考期末）定义：有一组邻边垂直且对角线相等的四边形称为垂等四边形．
（1）矩形 垂等四边形（填 “是”或“不是”）；
（2）如图1，在正方形中，点、、分别在、、上，四边形是垂等四边形，且，．
①求证：；
②若，求的值；
（3）如图2，在中，， 以为对角线，作垂等四边形．过点作的延长线的垂线，垂足为，且与相似，则四边形的面积是 ．
13．（2021·内蒙古赤峰·统考中考真题）数学课上，有这样一道探究题．
如图，已知中，AB=AC=m，BC=n，，点P为平面内不与点A、C重合的任意一点，将线段CP绕点P顺时针旋转a，得线段PD，E、F分别是CB、CD的中点，设直线AP与直线EF相交所成的较小角为β，探究的值和的度数与m、n、α的关系，请你参与学习小组的探究过程，并完成以下任务：
（1）填空：
【问题发现】
小明研究了时，如图1，求出了___________，___________；
小红研究了时，如图2，求出了___________，___________；
【类比探究】
他们又共同研究了α=120°时，如图3，也求出了；
【归纳总结】
最后他们终于共同探究得出规律：__________(用含m、n的式子表示)；___________ (用含α的式子表示)．
（2）求出时的值和的度数．