中考数学一轮复习过关练5.2 特殊平行四边形重难点题型讲练（讲练）（2份，原卷版+解析版）

这是一份中考数学一轮复习过关练5.2 特殊平行四边形重难点题型讲练（讲练）（2份，原卷版+解析版），文件包含中考数学一轮复习过关练52特殊平行四边形重难点题型讲练讲练原卷版doc、中考数学一轮复习过关练52特殊平行四边形重难点题型讲练讲练解析版doc等2份试卷配套教学资源，其中试卷共261页， 欢迎下载使用。
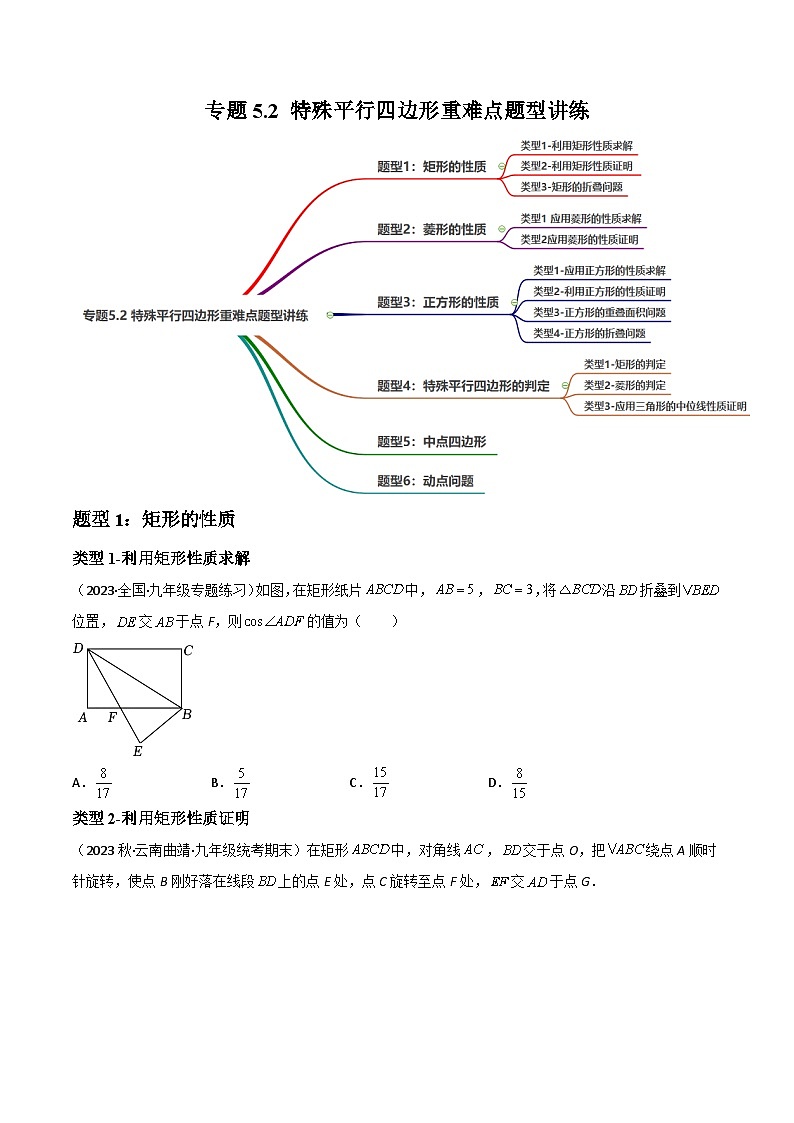
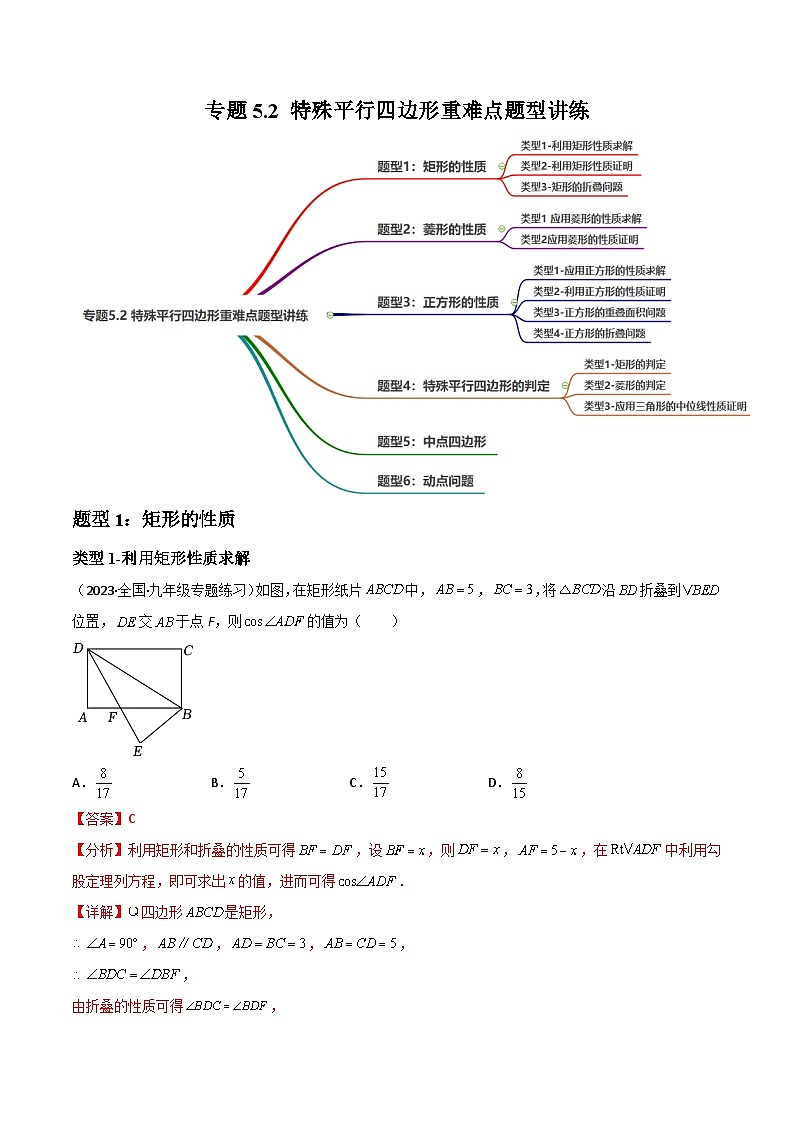
题型1：矩形的性质
类型1-利用矩形性质求解
（2023·全国·九年级专题练习）如图，在矩形纸片中，，，将沿折叠到位置，交于点F，则的值为（ ）
A．B．C．D．
类型2-利用矩形性质证明
（2023秋·云南曲靖·九年级统考期末）在矩形中，对角线，交于点O，把绕点A顺时针旋转，使点B刚好落在线段上的点E处，点C旋转至点F处，交于点G．
(1)求证：为等腰三角形；
(2)试判断与的关系，并说明理由．
类型3-矩形的折叠问题
25．（2023春·山西晋城·九年级校联考阶段练习）综合与实践
问题情境：综合与实践课上，老师让同学们以“矩形纸片的折叠”为主题开展数学活动．矩形纸片中，，．
操作探究：如图1，将矩形纸片沿过点A的直线折叠，使点D的对应点落在边上，展开后折痕交于点E．
(1)的度数为______．
(2)求线段的长度．
拓展延伸：
(3)如图2，在图1的基础上，继续沿过点A的直线折叠，使点B的对应点落在上，展开后折痕交于点F，连接．请判断的形状并说明理由．
综合训练
1．（2023春·湖南长沙·八年级长沙市长郡梅溪湖中学校考阶段练习）如图，在矩形中，对角线与相交于点，已知，则的大小是（ ）
A．B．C．D．
2．（2023春·重庆·九年级重庆一中校考阶段练习）如图，点E，F分别在矩形的边上，过A作交矩形对角线于点G，，，，则长度是（ ）
A．B．C．D．
3．（2023春·重庆沙坪坝·九年级重庆八中校考阶段练习）如图，四边形为矩形，且，，点E为上一点且，连接、，且，，连接，则的长为（ ）
A．10B．C．D．
4．（2023春·江苏·八年级专题练习）已知：如图，矩形中，，对角线相交于点O，点P是线段上任意一点，且于点E，于点F，则等于（ ）
A．6B．5C．D．
5．（2022秋·广东肇庆·八年级广东肇庆中学校考期末）已知：如图，折叠长方形的一边，使点D落在边的点E处，已知，，则的长是（ ）
A．B．2C．D．
6．（2023·黑龙江绥化·校考模拟预测）如图，在矩形中，，，点是上一个动点，把沿向矩形内部折叠，当点A的对应点恰好落在的平分线上时， 的长为（ ）
A．或B．4或C．或D．或
7．（2023春·江苏·八年级泰州市姜堰区第四中学校考周测）如图，在矩形中，对角线与相交于点O，过点A作的垂线，垂足为E．若，则____．
8．（2022秋·福建莆田·九年级校考期中）如图，矩形的四个顶点分别在直线，，，上．若直线且间距相等，，，则的值为______．
9．（2022·江西萍乡·校考模拟预测）如图，在矩形中，，，点P在矩形上或其对角线上运动，，则长为________．
10．（2023春·江苏·八年级泰州市姜堰区第四中学校考周测）如图，在矩形中，交于点O，于点E，，则的度数为_________
11．（2022春·北京东城·八年级校考阶段练习）如图，过矩形的对角线上一点K分别作矩形两边的平行线与，那么图中矩形的面积与矩形的面积的大小关系是_____；（填“＞”或“＜”或“=”）
12．（2023·河南周口·校考一模）如图，在矩形中，E为射线上一点，将沿翻折，使点B落在点F处，若，则BE＝_____．
13．（2023春·河北承德·九年级统考阶段练习）如图1，将矩形纸片对折，使与重合，得到折痕，把纸片展平；再一次折叠纸片，使点A落在上的点N处，并使折痕经过点B，得到折痕，把纸片展平，连接．
（1）图中是__________三角形；
（2）继续折叠纸片，使点A落在边上的点H处，并使折痕经过点B，得到折痕，把纸片展平，如图2，则__________，设与交于点P，若直线交直线于点O，，，则__________．
14．（2023秋·湖南湘西·九年级统考期末）如图，将矩形绕点旋转得到矩形，点在上，延长交于点.
(1)求证：；
(2)连接，若，求的度数．
15．（2022秋·浙江金华·九年级校考期中）如图，四边形是矩形，，，是上的一点，且，点是边上的任意一点．连接，将线段绕点顺时针旋转，得到线段．
(1)求点到的距离；
(2)当时，若此时点恰好落在对角线上，求的长．
16．（2023·安徽淮北·淮北一中校联考一模）已知矩形，将其绕着点逆时针旋转得到矩形．
(1)如图1，若点在上，连接．
①求证：平分；
②连接交于点，若，，求的长．
(2)如图2，若点，，在同一条直线上，与交于点，，，求的长．
17．（2023·山东青岛·校考一模）已知：线段和矩形如图①摆放（点E与点B重合），点F在边上，，．如图②．从图①的位置出发，沿方向运动，速度为；动点P同时从点D出发，沿方向运动，速度为．点M为的中点，连接，，，与相交于点Q，设运动时间为．解答下列问题：
(1)当时，求t的值；
(2)设五边形的面积为，求S与t的关系式；
(3)当时，求线段的长；
(4)当t为何值时，五边形的周长最小，最小是多少？直接写出答案即可．
18．（2023春·湖南长沙·八年级长沙县湘郡未来实验学校校考阶段练习）在平面直角坐标系中存在矩形，点、点，且、满足：（实数．
(1)求点坐标；
(2)如图1，作的角平分线交轴于，的中点为，作交轴于，求的值（用含式子表示）；
(3)如图2，在（2）的条件下，当时，将矩形向右推倒得到矩形，使与重合，落在轴上，现在将矩形沿射线以1个单位/秒平移，设平移时间为，用表示平移过程中矩形与矩形重合部分的面积．
19．（2023秋·辽宁沈阳·九年级统考期末）已知矩形的对角线，相交于点O，点E是边上一点，连接，，，且．求证：．
20．（2023·福建南平·统考一模）在五边形中，四边形是矩形，是以E为直角顶点的等腰直角三角形．与交于点G，将直线绕点E顺时针旋转交于点F．
(1)求证：；
(2)判断线段，，之间的数量关系，并说明理由；
(3)若，且，求线段的长．
21．（2023秋·四川眉山·九年级统考期末）如图，在矩形中，E是边的中点，于点F，连接．
(1)求证：；
(2)求证：．
22．（2022秋·四川达州·九年级统考期末）在矩形中，E为边上一动点，连接．

(1)将沿翻折，使点B恰好落在对角线上的点F处，AE交于点G．
①如图①，若，求证：F为的中点；
②如图②，当，时，求的长．
(2)根据②所得数据，将矩形沿翻折，点C的对应点为，点D的对应点为，使点E，，D三点在一条直线上，如图③，求此时的长．
题型2：菱形的性质
类型1 应用菱形的性质求解
（2022秋·吉林长春·九年级长春市解放大路学校校考开学考试）如图，在菱形中，的垂直平分线交于点为垂足，连接，则的度数是（ ）
A．B．C．D．
类型2应用菱形的性质证明
（2023·陕西西安·西安市铁一中学校考三模）如图，已知菱形，点F在的延长线上，点E在的延长线上，且满足．求证：是等边三角形．
综合训练
1．（2023·陕西西安·校考二模）如图，为菱形的对角线，已知，则等于（ ）
A．B．C．D．
2．（2022秋·广东梅州·九年级校考阶段练习）如图所示，在菱形 中，，， 分别是边 和 的中点， 于点 ，则 的度数是 （ ）
A．B．C．D．
3．（2022秋·广东揭阳·九年级统考期中）如图，菱形中，交于，于，连接，若，则的度数为（ ）
A．B．C．D．
4．（2023秋·重庆·九年级校考期末）如图，四边形是菱形，连接，交于点，过点作，交于点，若，，则的长度是（ ）
A．B．C．D．
5．（2023秋·陕西汉中·九年级统考期末）如图，在菱形中，对角线相交于点O，若，则的度数为________．
6．（2022秋·四川成都·九年级成都七中校考期中）如图，在菱形中，与相交于点，的垂直平分线交于点，连接，若，则的度数为______．
7．（2022·江西萍乡·校考模拟预测）如图，在菱形中，，为的中点，点在上，，，将沿方向平移，使点落在上，则平移的距离为________．
8．（2023·全国·九年级专题练习）如图，菱形纸片中，，，将纸片沿对角线剪开，再将沿射线的方向平移得到，当是直角三角形时，平移的距离为___．
9．（2023春·四川成都·九年级统考开学考试）如图，在菱形中，，，G为边上一动点，作于点，于点H，当取得最小值时，__________．
10．（2023·陕西西安·陕西师大附中校考模拟预测）如图，在菱形中，对角线与相交于点，过点作，交于点，若，，则的长是______．
11．（2023·陕西西安·交大附中分校校考三模）如图，菱形的顶点是原点，顶点在轴上，反比例函数的图象经过顶点．若菱形的面积为，则的值为________．
12．（2023春·四川成都·九年级统考开学考试）如图，菱形的边长为，其中对角线的长为，则菱形的面积为_________．
13．（2023·河南新乡·统考一模）如图，在菱形中，，，扇形的半径为6，圆心角为，则阴影部分的面积是______．
14．（2022·广东东莞·校考一模）如图，是菱形的对角线，．
(1)请用尺规作图法，作的垂直平分线，垂足为E，交于F；（不要求写作法，保留作图痕迹）
(2)在（1）条件下，连接，求的度数．
15．（2023秋·四川成都·九年级统考期末）如图，在菱形中，，点是边上一动点，连接，将射线绕点逆时针旋转60°，分别交边于点，交对角线于点.
(1)试判断的形状，并说明理由；
(2)若，，求及的长；
(3)若，求的值.
16．（2023春·江苏·八年级姜堰区实验初中校考周测）如图，已知菱形中，对角线、相交于点，过点作，过点作，与相交于点．
(1)求证：四边形是矩形；
(2)若，，则四边形的周长为 ．
17．（2023·四川巴中·校考一模）如图，在四边形中，，，对角线，交于点O，平分，过点C作交的延长线于点E，连接．
(1)求证：四边形是菱形；
(2)若，，求的长．
18．（2023秋·辽宁沈阳·九年级统考期末）如图，在菱形中，对角线，交于点O，，，连接，交于点F．
(1)求证：四边形是矩形；
(2)若，，直接写出菱形的面积．
19．（2023秋·山东济南·九年级统考期末）如图，矩形的对角线交于点F，延长到点C，使，延长到点D，使，连接
(1)求证：四边形是菱形；
(2)若，求菱形的面积．
20．（2022秋·山东菏泽·九年级统考期末）如图，在菱形中，点E、F分别在边上，且，连接，求证：．
21．（2023秋·广东河源·九年级校考期末）如图，在菱形中，对角线，交于点，交延长线于，交延长线于点．
(1)求证：四边形是矩形；
(2)若，，求AC的长．
22．（2023春·北京海淀·九年级人大附中校考开学考试）如图，在中，，D是的中点，点E，F在射线上，且．
(1)求证：四边形是菱形；
(2)点G为线段的中点，射线交于点H，若，求线段的长．
23．（2023秋·福建莆田·九年级莆田第二十五中学校考期末）如图，中，为的中点，连接，作点关于的对称点，连接．
(1)求证：四边形为菱形；
(2)连接，若平分，求的长
24．（2023秋·云南曲靖·九年级统考期末）如图，在菱形中，为菱形的一条对角线，以为直径作，交于点E，交于点F，G为边上一点，且．
(1)求证：为的切线；
(2)若，，求的半径．
题型3：正方形的判定
类型1-应用正方形的性质求解
（2023·陕西西安·交大附中分校校考三模）如图，在正方形中，点在对角线上，，，，分别为垂足，连结，，若，则（ ）
A．5B．C．D．
类型2-利用正方形的性质证明
（2023春·江苏·八年级姜堰区实验初中校考周测）如图，在正方形中，是边上点，（与、不重合），连接，将沿所在的直线折叠得到，延长交于，连接，作，与的延长线交于点，连接．
(1)求证：；
(2)求证：平分．
类型3-正方形的重叠面积问题
（2023·广东东莞·东莞市东华初级中学校考模拟预测）如图，将边长为4的正方形绕点按逆时针方向旋转，得到正方形，连接，在旋转角从0°到180°的整个旋转过程中，当时，的面积为____________．
类型4-正方形的折叠问题
（2023春·全国·八年级专题练习）如图，正方形中，，点E在边上，且．将沿对折至，延长交边于点G，连接、．
(1)求证：；
(2)求的面积；
(3)在的条件下，求周长的最小值．
综合训练
1．（2022·陕西西安·西安市第三中学校考模拟预测）下列四边形中，对称轴条数最多的四边形是（ ）
A．平行四边形B．等腰梯形C．菱形D．正方形
2．（2023·云南昆明·昆明八中校考模拟预测）如图，有六根长度相同的木条，小明先用四根木条制作了能够活动的菱形学具，他先将该活动学具调成图1所示菱形，测得，对角线，接着将该活动学具调成图2所示正方形，最后用剩下的两根木条搭成了如图3所示的图形，连接，则图3中的面积为（ ）
A．B．C．D．
3．（2023秋·重庆江北·九年级统考期末）如图，已知正方形中，，，则的度数是（ ）
A．B．C．D．
4．（2023秋·山东烟台·八年级统考期末）如图，P为线段上任意一点，分别以、为边在同侧作正方形、，若，则的度数为（ ）
A．B．C．D．
5．（2023春·八年级单元测试）如图，E、F、H分别为正方形的边、、上的点，连接，，且，平分交于点G．若，则的度数为（ ）
A．26°B．38°C．52°D．64°
6．（2022秋·重庆·九年级统考期末）如图，在正方形中，点M是上一点，点E是的中点，绕点E顺时针旋转得到，连接，．则的度数为（ ）
A．B．C．D．
7．（2023秋·河北唐山·九年级统考期末）如图，四边形是正方形，是上一点，，将绕着点顺时针旋转到与重合，，则正方形的边长为（ ）
A．B．C．5D．4
8．（2022秋·贵州黔东南·九年级统考期末）如图，在边长为6的正方形内作，交于点E，交于点F，连接，将绕点A顺时针旋转到的位置，点D的对应点是点B．若，则的长为（ ）
A．B．C．D．2
9．（2022秋·山西朔州·九年级统考期末）如图．正方形的边长为4．以C为圆心，长为半径画弧，交于点F，若再以C为圆心，长为半径画弧，交的延长线于点E，则图中阴影部分的面积为（ ）
A．B．C．D．
10．（2023春·八年级课时练习）如图，已知正方形ABCD的边长为4，E是AB边延长线上一点，BE＝2，F是AB边上一点，将△CEF沿CF翻折，使点E的对应点G落在AD边上，连接EG交折痕CF于点H，则FH的长是（ ）
A．B．C．1D．
11．（2022秋·辽宁沈阳·九年级统考期末）如图，正方形的面积为12，点E在边上，且，连接将沿折叠，点A对应点为F，延长交于点G，点M，N分别是，的中点，则的长为（ ）
A．B．C．D．
12．（2023·山东青岛·统考一模）如图，在正方形中，，为的中点，将沿折叠，使点落在正方形内点处，连接，则的长为（ ）
A．B．C．D．
13．（2022春·湖南永州·八年级校考期中）如图所示，以正方形中边为一边向外作等边，则__．
14．（2023·安徽·校联考一模）如图．已知正方形纸片的边，点P在边上，将沿折叠，点A的应点为．
（1）若时，的长为______﹔
（2）若点到边或的距离为1，则线段的长为______．
15．（2023·湖北孝感·统考一模）数学课上，老师将如图边长为2的正方形铁丝框变形成以A为圆心，为半径的扇形（铁丝的粗细忽略不计），则所得扇形的面积是______．
16．（2023秋·重庆忠县·八年级统考期末）如图所示，若大正方形与小正方形的面积之差是20，则与的面积之和是_________
17．（2023秋·河北石家庄·八年级统考期末）如图，矩形内三个相邻的正方形面积分别为4，3和2，则图中阴影部分的面积为_______．
18．（2023秋·河北唐山·八年级校考期末）如图，有一块边长为2的正方形塑料模板ABCD，将一块足够大的直角三角板的直角顶点落在A点，两条直角边分别与CD交于点F，与CB延长线交于点E，则四边形AECF的面积是___________．
19．（2023秋·江苏南京·九年级统考期末）如图，正方形的边长为，点是边的中点，点是边上一动点，连接，将沿翻折得到，连接，当最小时，的长是______．
20．（2023春·江苏·八年级专题练习）如图，折叠边长为4cm的正方形纸片，折痕是，点C落在点E处，分别延长、交于点F、G，若点M是边的中点，则______cm．
21．（2023春·江苏·八年级专题练习）如图，正方形纸片的边长为12，E是边上一点，连接，折叠该纸片，使点A落在上的G点，并使折痕经过点B，折痕与交于点H，点F在上，若，则的长为_____．
22．（2023春·八年级课时练习）如图，点E在正方形外，连接，过点A作的垂线交于点F．若．则下列结论：
①；
②；
③点B到直线的距离为；
④．
其中正确的结论是________.（填写所有正确结论的序号）
23．（2023·浙江·模拟预测）如图，正方形的边长为，E，F分别是的中点，与分别交于点M，N． 请你回答下列问题：
(1)求证：．
(2)直接写出的长．
(3)求的面积．
24．（2023春·江苏·八年级泰州市姜堰区第四中学校考周测）如图，正方形的顶点C在直线a上，且直线a于M，直线a于N．
(1)求证：
(2)若点B，D到a的距离分别是1，2，求正方形的面积．
25．（2023春·重庆·九年级重庆一中校考阶段练习）如图，正方形的对角线和交于点O，点E是上的一点，．
(1)用直尺和圆规完成以下基本操作：过点B作的角平分线交和分别于点F和点G（保留作图痕迹，不写作法）：
(2)求证：．
证明：在正方形中，，
∵，平分
∴______①
∴
又∵
∴
∴______②
在和中，
∴
∴______④
∴
26．（2023春·江苏·八年级姜堰区实验初中校考周测）如图，四边形是正方形，是等腰三角形，，．连接，过B作于F，连接，．
(1)若，求的度数；
(2)当变化时，的大小会发生变化吗?请说明理由；
(3)试用等式表示线段与之间的数量关系，并证明．
27．（2023秋·辽宁阜新·九年级阜新实验中学校考期末）如图，正方形和正方形（其中），的延长线与直线交于点H．
(1)如图1，当点G在上时，求证：；
(2)将正方形绕点C旋转一周．
①如图2，当点E在直线右侧时，判断的数量关系并证明；
②当时，若，请直接写出线段的长．
28．（2022秋·四川广安·九年级统考阶段练习）如图，已知E是正方形的边上的一点，延长到点F使，连接，．
(1)能通过旋转得到吗？说明理由．
(2)连接，过点D作垂直于点M，交于点N．若，，求的长．
29．（2023·陕西西安·西安市铁一中学校考三模）如图，在正方形中，点P在边上，且不与点A，D重合，点H在边上，且不与点A，B重合，连接与交于点E.若，求证：
30．（2022秋·辽宁沈阳·九年级统考期末）如图，在正方形中，E、F分别是和上的动点，且．
(1)求证：；
(2)若平分，且正方形的面积为36，连接，点P为线段上一个动点，，，垂足分别为G、H．则_____．
31．（2022春·福建龙岩·八年级校考期中）如图1，在正方形中，点E是边上的一点，，且交正方形外角的平分线于点P．
(1)求的度数；
(2)求证：；
(3)在边上是否存在点M，使得四边形是平行四边形？若存在，请画出图形并给予证明；若不存在，请说明理由；
(4)如图2，在边长为4的正方形中，将线段沿射线平移，得到线段，连接，则直接写出的最小值是 ．
题型4：特殊平行四边形的判定
类型1-矩形的判定
（2023春·八年级课时练习）如图，平行四边形的对角线相交于点O，请你再添一个条件，使得平行四边形是矩形，则下列条件符合的是( )
A．平分B． C． D．
25．（2023春·江苏·八年级姜堰区实验初中校考阶段练习）如图，在平行四边形中，于点，延长至点，使，连接，与交于点．
(1)求证：四边形为矩形；
(2)若，求的长．
类型2-菱形的判定
（2023秋·河北保定·九年级统考期末）如图，甲、乙两人分别用一张矩形纸做一个折菱形的游戏．甲沿折叠使得点落在上，沿折叠使得点落在上，甲说得到的四边形为菱形；乙沿折叠使得与重合，再折出，，乙说得到的四边形为菱形；下列说法正确的是（ ）
（2023春·全国·八年级阶段练习）如图，矩形，延长至点E，使，连接，过点C作交的延长线于点F，连接．
(1)求证：四边形是菱形；
(2)连接交于点G．当，时，求的长．
类型3-正方形的判定
（2023春·全国·八年级专题练习）如图，在中，点E、D、F分别在边上，且，，下列四个判断中，不正确的是（ ）
A．四边形是平行四边形
B．如果平分，那么四边形是菱形
C．如果，那么四边形是矩形
D．如果且，那么四边形是正方形
（2023秋·山东烟台·八年级统考期末）问题情境：
如图1，点为正方形内一点，，将绕点按顺时针方向旋转，得到 （点的对应点为点）．延长交于点，连接，
猜想证明：
(1)试判断四边形的形状，并说明理由；
(2)如图2，若、请猜想线段与的数最关系并加以证明，解决问题；
(3)如图1，若的面积为72，，请直接写出的长．
综合训练
1．（2023秋·辽宁朝阳·九年级统考期末）如图，四边形是平行四边形，下列结论中错误的是（ ）
A．当，是矩形B．当，是菱形
C．当，是菱形D．当，是正方形
2．（2023春·江苏·八年级专题练习）如图，要使平行四边形为矩形，则可添加下列哪个条件（ ）
A． B． C． D．
3．（2022秋·河南平顶山·九年级校考期中）如图，在平行四边形ABCD中，在不添加任何辅助线的情况下，添加以下哪个条件，能使平行四边形ABCD是矩形（ ）
A．B．C．D．
4．（2023春·全国·八年级专题练习）顺次连接四边形ABCD各边的中点，得到四边形EFGH，在下列条件中，能使四边形EFGH为矩形的是（ ）
A．AB＝CDB．AB⊥CDC．AC⊥BDD．
5．（2022秋·福建福州·八年级福建省福州第十六中学校考期末）已知四边形ABCD是平行四边形，下列结论中错误的是（ ）
A．当∠ABC=90°时，它是矩形B．当AB=BC时，它是菱形
C．当AC⊥BD时，它是菱形D．当AC=BD时，它是正方形
6．（2023秋·贵州六盘水·九年级统考期末）如图，在中，对角线，相交于点O，若添加一个条件，使得一定为菱形，该条件是（ ）
A．B．C．D．
7．（2022秋·四川南充·九年级校考阶段练习）如图，在▱ABCD中，O为AC的中点，经过点O的直线交AD于E交BC于F，连接AF、CE，下列选项可以使四边形AFCE是菱形的为（ ）
A．OE＝OFB．AE＝CFC．EF⊥ACD．EF＝AC
8．（2021秋·山东菏泽·九年级校考阶段练习）如图，平行四边形 ABCD 的对角线 AC、BD 相交于点 O，那么下列条件中，能判断平行四边形 ABCD 是菱形的为 （ ）
A．AO＝COB．AO＝BOC．∠AOB＝90°D．∠BAD＝∠ABC
9．（2022春·上海杨浦·八年级校考期末）顺次连接四边形各边中点得到的四边形是菱形，那么与只需满足（ ）
A．垂直B．相等C．互相平分D．互相平分且垂直
10．（2023·广西防城港·校考一模）如图，在正方形中，对角线，交于点O，点E，F分别在，上，且，交于点G，连接．下列结论错误的是（ ）
A．B．
C． D．四边形是菱形
11．（2023春·河北承德·九年级统考阶段练习）如图，中，点E、F在对角线上，且，要使四边形为菱形，现有甲、乙、丙三种方案：
甲：只需要满足；
乙：只需要满足；
丙：只需要满足．
则正确的方案是（ ）
A．甲、乙、丙B．甲、丙C．甲、乙D．乙、丙
12．（2023秋·山西晋中·九年级统考期末）如图，在菱形中，对角线，相交于点，添加下列条件，能使菱形成为正方形的是（ ）
A．B．C．D．平分
13．（2023秋·福建漳州·九年级统考期末）如图，在矩形中，对角线，交于点O，要使该矩形成为正方形，则应添加的条件是（ ）
A．B．
C．D．
14．（2023春·八年级课时练习）如图，在矩形内有一点，与分别平分和，点为矩形外一点，连接，，若，则添加下列条件不能判定四边形是正方形的是（ ）
A．B．C．D．
15．（2022秋·辽宁辽阳·九年级校联考期中）有下列四个条件：①；②；③；④；从中选两个作为补充条件，使平行四边形为正方形，现有下列四种选法，你认为错误的是（ ）
A．①②B．①③C．②③D．②④
16．（2023·湖南湘潭·湘潭县云龙中学校考一模）如图，平行四边形添加一个条件_____使得它成为矩形．（任意添加一个符合题意的条件即可）
17．（2022秋·山西晋中·九年级统考期末）平行四边形的对角线与相交于点，若要使平行四边形成为矩形，则需要添加的一个条件是___________．（只写出一种情况即可）
18．（2023秋·山西运城·九年级统考期末）如图，已知四边形是菱形，从①，②，③中选择一个作为条件后，使四边形成为正方形，则应该选择的是______．（仅填序号）
19．（2022春·山东济宁·八年级校考期末）如图，已知点D在△ABC的BC边上，DEAC交AB于E，DFAB交AC于F，若添加条件_____，则四边形AEDF是矩形；若添加条件_____，则四边形AEDF是菱形；若添加条件_____，则四边形AEDF是正方形．
20．（2023春·全国·八年级专题练习）如图，AD是△ABC的中线，过点A作AEBC，过点B作BEAD交AE于点E．
(1)求证：∠E＝∠ADB．
(2)当△ABC满足 条件时，四边形ADBE是矩形？请说明理由．
21．（2022春·河北石家庄·八年级校考期末）如图，在平行四边形中，对角线与交于点O.
(1)添加一个条件：_____，则可判定四边形是矩形；
(2)若，，则与的周长之差为_____________.
22．（云南省楚雄州部分地区2022-2023学年九年级下学期教学质量作业四（开学考）数学试题）如图，四边形中，是对角线，，且，于点D，点E、F分别是边、的中点，连接、分别交于点G、H．
(1)求证：四边形是矩形；
(2)若，求的面积．
23．（2023春·八年级课时练习）如图，已知，延长到E，使，连接，，，若．
(1)求证：四边形是矩形；
(2)连接，若，，求的长．
24．（2023春·江苏·八年级校考周测）如图，在中，是上的任意一点（不与点、重合），过点平行于的直线分别与、的外角的平分线交于点、．
(1)与相等吗？证明你的结论．
(2)试确定点的位置，使四边形是矩形，并加以证明．
25．（2023秋·河南平顶山·九年级统考期末）如图，在中，，D为的中点，四边形是平行四边形．
(1)判断四边形的形状，并说明理由；
(2)填空：
①当且时，四边形的周长等于______；
②当时，四边形的形状为______．
26．（2023·广东深圳·校考一模）如图，已知中，是边上一点，过点分别作交于点，作交于点，连接．
(1)下列条件：
①是边的中点；
②是的角平分线；
③点与点关于直线对称．
请从中选择一个能证明四边形是菱形的条件，并写出证明过程；
(2)若四边形是菱形，且，，求的长．
27．（2023秋·河南郑州·九年级校考期末）如图，在平行四边形中，对角线，相交于点O，点E，F在上，且．
(1)求证：；
(2)不添加辅助线，请你补充一个条件，使得四边形是菱形；并给予证明．
28．（2022秋·河南郑州·九年级校考期末）如图，已知在中，，，，点、分别从点、出发沿、方向向点A、C匀速运动，运动速度均为，当点到达点时，两点都停止运动．以、为边作平行四边形，连接，交于点设运动的时间为．
(1)求四边形的最大面积．
(2)填空：
①当______时，四边形是矩形；
②当______时，四边形是菱形．
29．（2023春·江苏·八年级姜堰区实验初中校考周测）如图，在四边形中，，，对角线、交于点，平分，过点作交延长线于点，连接．
(1)求证：四边形是菱形；
(2)若，，求的长．
30．（2023·黑龙江绥化·校考模拟预测）如图，在梯形中，，，，，，动点从点开始沿边向以秒的速度运动，动点从点开始沿边向以秒的速度运动，、分别从、同时出发，当其中一点到端点时，另一点也随之停止运动，设运动时间为秒．问：
(1)求为何值时，四边形是平行四边形？
(2)四边形可能是矩形吗？如果可能，求出的值；如果不可能，说明理由；
(3)四边形可能是菱形吗？如果可能，求出的值；如果不可能，说明理由．
31．（2023秋·山东济南·九年级统考期末）如图，矩形的对角线交于点F，延长到点C，使，延长到点D，使，连接
(1)求证：四边形是菱形；
(2)若，求菱形的面积．
32．（2023·全国·九年级专题练习）如图，中， 是边上的中线，分别过点作的平行线交于点且交于点连接
(1)求证：四边形是菱形；
(2)若 求菱形的面积．
33．（2023春·江苏·八年级泰州市姜堰区第四中学校考周测）如图，在四边形中，，过对角线的中点O，作，分别交边，于点E，F，连接，．
(1)求证：四边形是菱形；
(2)若，，求四边形的面积．
34．（2022秋·广东东莞·八年级阶段练习）如图，矩形的对角线，相交于点，关于的对称图形为．
(1)求证：四边形是菱形；
(2)连接，若，．求的值；
35．（2023春·江苏·八年级校考周测）如图，矩形中，点P是线段上一动点，O为的中点，的延长线交于Q．
(1)求证：；
(2)若厘米，厘米，P从点A出发，以1厘米/秒的速度向D运动（不与D重合），设点P运动时间为t秒，请用t表示的长；并求t为何值时，四边形是菱形．
36．（2022春·福建龙岩·八年级校考期中）如图，平行四边形中，，过点作，交的延长线于点．
(1)求证：四边形是菱形；
(2)连接，若，，则的长为 ．
37．（2023春·江苏·八年级姜堰区实验初中校考周测）如图，在四边形中，，对角线的垂直平分线与边、分别相交于点M、N，连接、．
(1)求证：四边形是菱形；
(2)若四边形的周长为52，，求的长．
38．（2022秋·河南郑州·九年级校联考期末）如图，矩形中，，点M，N分别为上一点，且，连接．
(1)当时，求证：四边形是菱形；
(2)填空：①当 时，四边形是矩形；②当 时，以为对角线的正方形的面积为．
39．（2023春·全国·八年级专题练习）如图，中，是的平分线，作交于点，交于点F．
(1)求证：四边形是菱形；
(2)当满足条件 时，四边形是正方形．
40．（2023秋·陕西榆林·九年级统考期末）如图，在矩形中，对角线相交于点O．
(1)若，求证：矩形是正方形；
(2)请添加一个异于（1）的条件，使矩形成为正方形，不用说明理由．
41．（2023春·全国·八年级专题练习）如图，，是的两条中位线．我们探究的问题是：这两条中位线和三角形的两条边所围成的四边形的形状与原三角形的边或角有什么关系？建议按下列步骤探索：
(1)围成的四边形是否必定是平行四边形？
(2)在什么条件下，围成的四边形是菱形？
(3)在什么条件下，围成的四边形是矩形？
(4)你还能发现其他什么结论吗？
42．（2022春·湖南永州·八年级校考期中）如图，在中，，，垂足为点是外角的平分线，，垂足为点．
(1)求证：四边形为矩形；
(2)当满足什么条件时，四边形为正方形？给出证明．
43．（2023秋·山东枣庄·九年级统考期末）如图，在中，，过点C的直线，D为边上一点，过点D作，交直线与E，垂足为F，连接，．
(1)求证：；
(2)当D在中点时，四边形是什么特殊四边形？说明理由；
(3)在满足（2）的条件下，当满足______条件时，四边形是正方形（直接填写答案）．
题型5：中点四边形
（2023春·全国·八年级专题练习）已知：如图，四边形四条边上的中点分别为、、、，顺次连接、、、，得到四边形即四边形的中点四边形．
(1)四边形的形状是______，请证明你的结论；
(2)当四边形的对角线满足______条件时，四边形是菱形；
(3)你学过的哪种特殊的平行四边形的中点四边形是菱形？请写出一种．
综合训练
1．（2023春·湖南长沙·八年级长沙市长郡梅溪湖中学校考阶段练习）如图，在矩形中，对角线与相交于点，已知，则的大小是（ ）
题型5：中点四边形
（2023春·全国·八年级专题练习）已知：如图，四边形四条边上的中点分别为、、、，顺次连接、、、，得到四边形即四边形的中点四边形．
(1)四边形的形状是______，请证明你的结论；
(2)当四边形的对角线满足______条件时，四边形是菱形；
(3)你学过的哪种特殊的平行四边形的中点四边形是菱形？请写出一种．
综合训练
1．（2023春·福建福州·八年级校考阶段练习）如图，E，F，G，H分别是，，，的中点，且，下列结论：①四边形是菱形；②；③若，则；④；其中正确的个数是（ ）
A．1个B．2个C．3个D．4个
2．（2023春·八年级课时练习）如图所示，顺次连接四边形各边中点得到四边形，使四边形为正方形，应添加的条件分别是（ ）
A．且B．且
C．且D．且
3．（2023春·全国·八年级专题练习）顺次连接四边形四条边的中点，所得的四边形是菱形，则原四边形一定是( )
A．平行四边形B．对角线相等的四边形
C．矩形D．对角线互相垂直的四边
4．（2022秋·广东清远·九年级统考期中）如图，四边形中，E、F、G、H分别是、、、的中点，若中点四边形是菱形，那么原四边形满足什么条件（ ）
A．B．
C．D．
5．（2023秋·陕西西安·九年级统考期末）如图，是内一点，，，，，、、、分别是、、、的中点，则四边形的周长是（ ）
A．B．C．D．
6．（2022·广东佛山·校考一模）如图，点E，F，G，H分别为四边形ABCD四条边AB，BC，CD，DA的中点，则关于四边形EFGH，下列说法正确的是（ ）
A．不一定是平行四边形B．当AC＝BD时，它为菱形
C．一定是轴对称图形D．不一定是中心对称图形
7．（2022春·全国·八年级校考期末）如图，四边形中，E，F，G，H分别是边、、、的中点．若四边形为菱形，则对角线、应满足条件_______．
8．（2022秋·福建漳州·九年级漳州实验中学校考期中）如图，四边形中，E，F、G、H分别是边，、、的中点，请你添加一个条件，使四边形为菱形，应添加的条件是_____________．
9．（2023春·江苏·八年级专题练习）如图，已知矩形的对角线的长为10cm，顺次连接各边中点E、F、G、H得四边形，则四边形的周长为______cm．
10．（2022秋·贵州贵阳·九年级统考期末）如图，在矩形中，E，F，G，H分别是各边的中点，连接，，，．试判断四边形的形状，并说明理由．
题型5：特殊平行四边形的动点问题
（2023·全国·九年级专题练习）如图,在矩形ABCD中，，，动点M以的速度从A点出发,沿向点B运动,同时动点N以的速度从点D出发,沿DA向点A运动，设运动的时间为秒（）．
(1)当为何值时，的面积等于矩形面积的？
(2)是否存在某一时刻,使得以A、M、N为顶点的三角形与相似?若存在,求出的值;若不存在,请说明理由．
综合训练
1．（2022春·湖南永州·八年级校考期中）如图，在梯形中，，，动点P从点A开始，沿边，以1厘米/秒的速度向点D运动；动点Q从点C开始，沿边，以3厘米/秒的速度向B点运动．已知P、Q两点分别从A、C同时出发，当其中一点到达端点时，另一点也随之停止运动．假设运动时间为t秒，问：
(1)t为何值时，四边形是平行四边形？
(2)在某个时刻，四边形可能是菱形吗？为什么？
(3)t为何值时，四边形是等腰梯形？
2．（2023秋·辽宁沈阳·九年级统考期末）如图，在平面直角坐标系中，O是坐标原点，矩形的两边分别在x轴和y轴上，点B的坐标为，现有两动点P，Q，点P以每秒3个单位的速度从点O出发向终点A运动，同时点Q以每秒2个单位的速度从点A出发向终点B运动，连接，，．设运动时间为t秒（）．
(1)点P的坐标为______，点Q的坐标为______（用含t的代数式表示）；
(2)请判断四边形的面积是否会随时间t的变化而变化，并说明理由；
(3)若以A，P，Q为顶点的三角形与相似时，请直接写出t的值．
3．（2023春·辽宁沈阳·九年级统考开学考试）如图，在平面直角坐标系中，直线交x轴正半轴于点A，交y轴正半轴于点E，，，点C为射线上一点且纵坐标为8，连接，过点C作轴，过点A作交于点B．
(1)请直接写出直线的函数表达式；
(2)试判断四边形的形状，并说明理由；
(3)点F在，上运动，现从点C出发，沿路线向点A以每秒2个单位的速度匀速运动，设运动时问为t（秒），连接EF，EB
①当时，请直接写出的面积S与运动时间的函数关系式；
②请直接写出的面积为9时t的值；
4．（2022秋·四川眉山·九年级校考阶段练习）如图，已知正方形的边长为，动点从点出发，以的速度沿方向向点运动，动点从点出发，以的速度沿方向向点运动，若、两点同时出发运动时间为．
(1)连接、、，求当为何值时，的面积为？
(2)当点P在上运动时，是否存在这样的t使得是以为一腰的等腰三角形？若存在，请求出符合条件的t的值；若不存在，请说明理由．
5．（2022秋·福建泉州·九年级统考期末）如图，在中，，，，动点P从点A出发，沿线段向点B以的速度运动，同时动点Q从点C出发，沿线段向点A以的速度运动．当其中一点到达端点时，两点同时停止运动．以、为邻边作平行四边形．设平行四边形与重叠部分的图形面积为，运动时间为．
(1)当点E落在线段上时，求t的值；
(2)求S与t之间的函数关系式，并写出自变量t的取值范围；
(3)当四边形为菱形时，求t的值．
6．（2022秋·江西抚州·九年级校考期末）如图，在中，，平分，过点作的平行线交的延长线于点，连接．
(1)求证：四边形是菱形；
(2)如果，的长单位：米）是的两根，求的长以及菱形的面积；
7．（2022秋·山东青岛·九年级校考期中）如图，矩形中，，，点P从点A出发沿AB向点B移动（不与点A，B重合），一直到达点B为止；同时，点Q从点C出发沿向点D移动（不与点C，D重合）．运动时间设为t秒．
(1)若点P，Q均以的速度移动，则___________；___________．（用含t的代数式表示）
(2)在（1）的条件下，t为何值时，P，Q间的距离为？
(3)若点P为的速度移动，点Q以的速度移动，经过多长时间，使为等腰三角形？
(4)若点P，Q均以的速度移动，经过多长时间，四边形为菱形？
8．（2022秋·山东聊城·八年级校考期末）已知正方形中，，．动点以每秒2个单位速度从点出发沿线段方向运动，动点同时以每秒8个单位速度从点出发沿正方形的边方向顺时针作折线运动，当点与点相遇时停止运动，设点的运动时间为．
(1)当运动时间为__ 秒时，点P与点Q相遇；
(2)当时，求线段的长度；
(3)连接，当和全等时，求的值．
9．（2022秋·吉林白城·八年级校考阶段练习）如图，已知正方形中，边长为，点在边上，．点在线段上以/秒的速度由点向点运动，同时，点在线段上以厘米/秒的速度由点向点运动，设运动的时间为秒．
(1) ， ．（用含的代数式表示）
(2)若以、、为顶点的三角形和以、、为顶点的三角形全等，求的值．
10．（2022秋·吉林长春·九年级校考期末）如图，在中，，，，是的中点．动点从点出发，沿以每秒5个单位的速度向点运动，连接，以、为邻边作．设点的运动时间为（秒）．
(1)的长是______．
(2)当与的斜边垂直时，求的值．
(3)当是轴对称图形时，求的值．
(4)作点关于直线的对称点．当与的某一条直角边垂直时，直接写出的值．