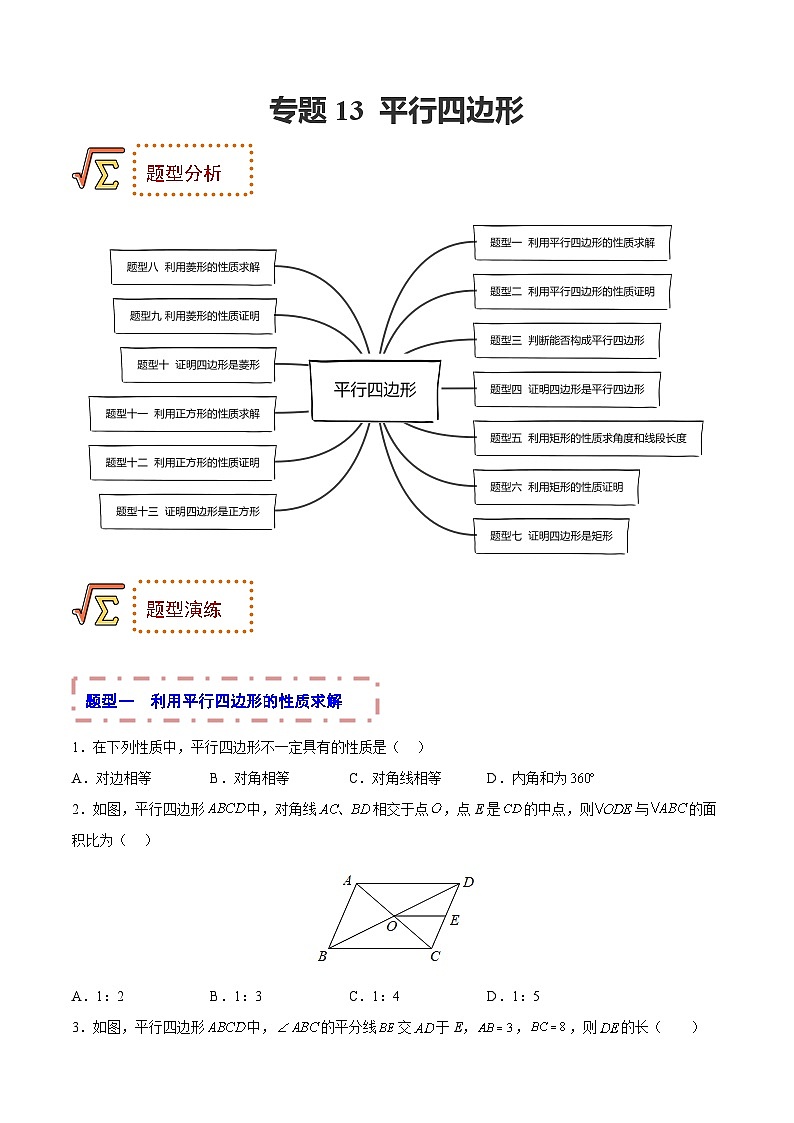
中考数学一轮复习考点题型归纳讲练专题13 平行四边形（2份，原卷版+解析版）

这是一份中考数学一轮复习考点题型归纳讲练专题13 平行四边形（2份，原卷版+解析版），文件包含中考数学一轮复习考点题型归纳讲练专题13平行四边形原卷版doc、中考数学一轮复习考点题型归纳讲练专题13平行四边形解析版doc等2份试卷配套教学资源，其中试卷共106页， 欢迎下载使用。

题型演练
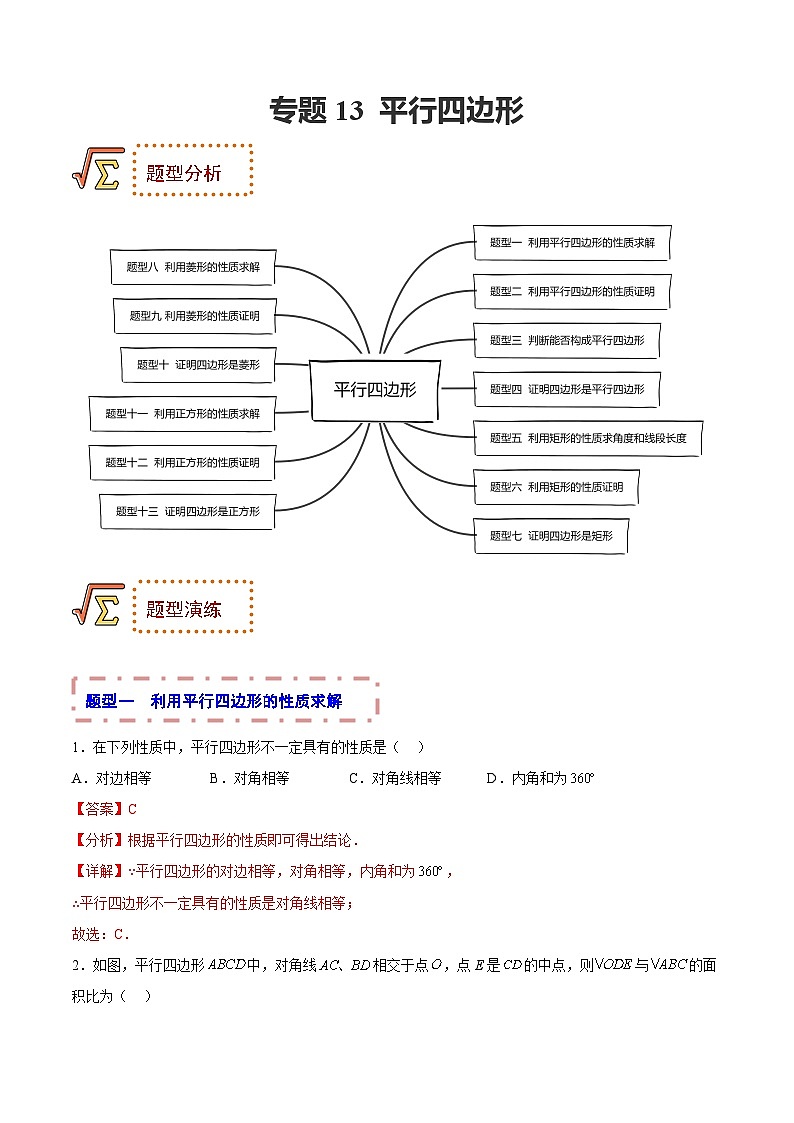
题型一 利用平行四边形的性质求解
1．在下列性质中，平行四边形不一定具有的性质是（ ）
A．对边相等B．对角相等C．对角线相等D．内角和为
2．如图，平行四边形中，对角线相交于点，点E是的中点，则与的面积比为（ ）
A．1：2B．1：3C．1：4D．1：5
3．如图，平行四边形中，的平分线交于E，，，则的长（ ）
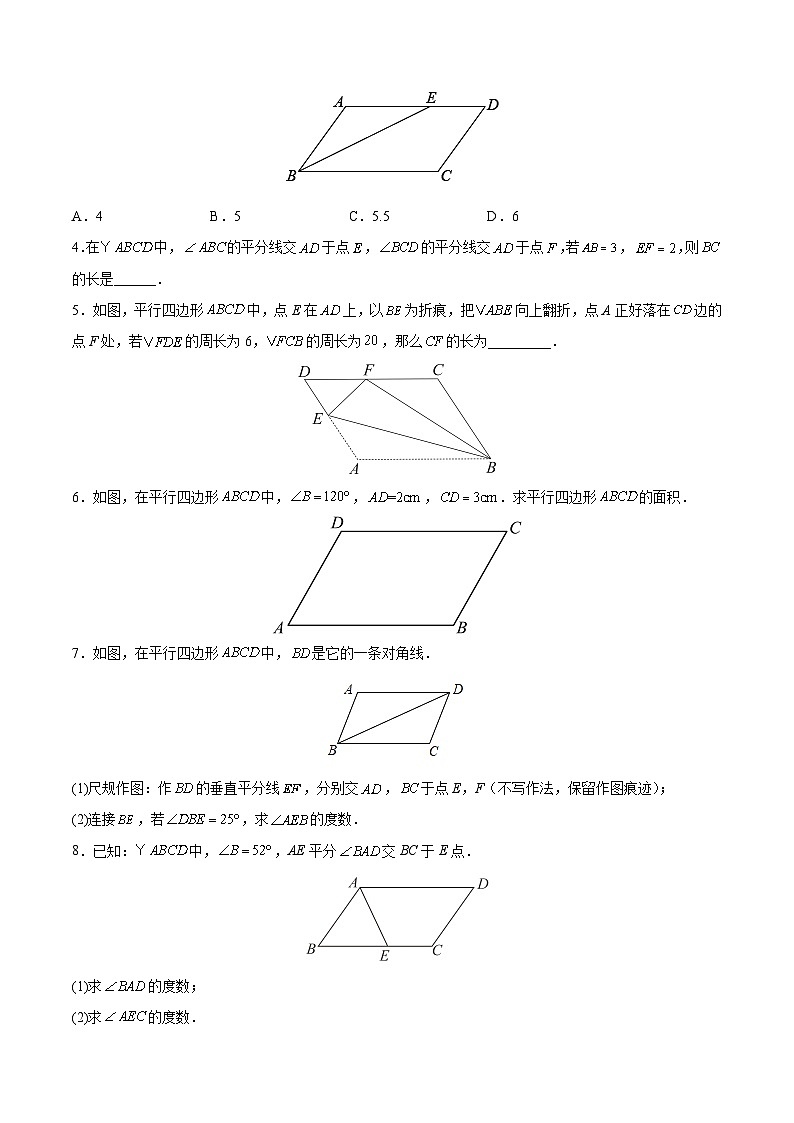
A．4B．5C．5.5D．6
4．在中，的平分线交于点，的平分线交于点，若，，则的长是______．
5．如图，平行四边形中，点E在上，以为折痕，把向上翻折，点A正好落在边的点F处，若的周长为6，的周长为，那么的长为_________．
6．如图，在平行四边形中，，，．求平行四边形的面积．
7．如图，在平行四边形中，是它的一条对角线．
(1)尺规作图：作的垂直平分线，分别交，于点E，F（不写作法，保留作图痕迹）；
(2)连接，若，求的度数．
8．已知：中，，AE平分交BC于E点．
(1)求的度数；
(2)求的度数．
题型二 利用平行四边形的性质证明
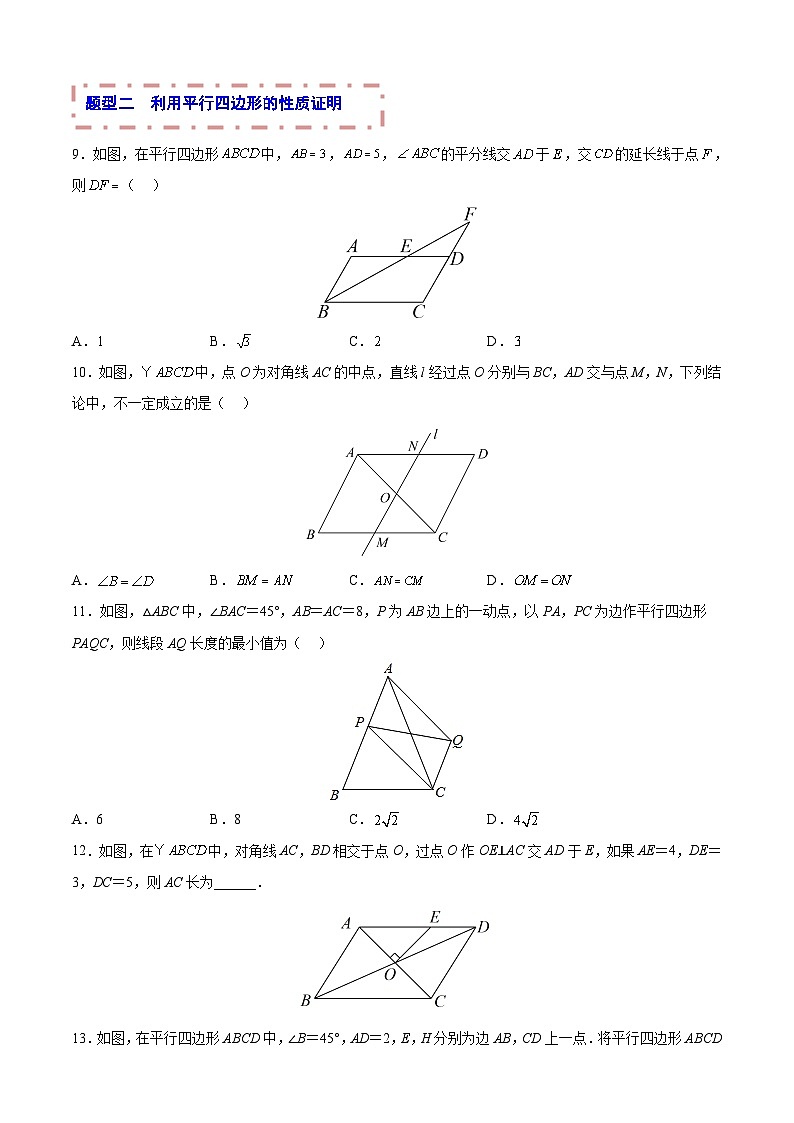
9．如图，在平行四边形中，，，的平分线交于，交的延长线于点，则（ ）
A．B．C．D．
10．如图，中，点O为对角线AC的中点，直线l经过点O分别与BC，AD交与点M，N，下列结论中，不一定成立的是（ ）
A．B．C．D．
11．如图，△ABC中，∠BAC＝45°，AB＝AC＝8，P为AB边上的一动点，以PA，PC为边作平行四边形PAQC，则线段AQ长度的最小值为（ ）
A．6B．8C．D．
12．如图，在中，对角线AC，BD相交于点O，过点O作OE⊥AC交AD于E，如果AE＝4，DE＝3，DC＝5，则AC长为______．
13．如图，在平行四边形ABCD中，∠B＝45°，AD＝2，E，H分别为边AB，CD上一点．将平行四边形ABCD沿EH翻折，使得AD的对应线段FG经过点C，若FG⊥CD，C为FG的中点，则EF的长度为 _____．
14．已知：如图，在平行四边形中，点、为对角线上两点，且求证：．
15．如图，在中，．
(1)用尺规完成以下基本作图：在上截取，使；作的平分线交于点F．（保留作图痕迹，不写作法）
(2)在（1）所作的图形中，连接交于点G，证明：．
16．如图，在▱ABCD中，DE⊥AC于E，BF⊥AC于F，∠DAE＝35°．
(1)求证：△AED≌△CFB；
(2)求∠CBF的度数．
17．如图，在平行四边形ABCD中，AC⊥DE，AE=AD，AE交BC于O．
(1)求证：∠BCA=∠EAC；
(2)若CE=3，AC=4，求COE的周长．
18．如图，在平行四边形中，，是对角线，是的平分线，交边的延长线于点．
(1)证明：；
(2)若，，写出图中长度等于的所有线段．
题型三 判断能否构成平行四边形
19．下列命题中，真命题的是（ ）
A．一组对角相等且一组对边相等的四边形是平行四边形
B．一组对边平行且一组对角互补的四边形是平行四边形
C．两组对角分别相等的四边形是平行四边形
D．一组邻边相等且一组对边平行的四边形是平行四边形
20．下列四组条件中，不能判定四边形ABCD是平行四边形的是（ ）．
A．AB＝DC，AD＝BCB．
C．，AB＝DCD．，AD＝BC
21．如图，四边形ABCD的对角线AC和BD相交于点O，下列不能判定四边形ABCD为平行四边形的条件是（ ）
A．B．
C．D．
22．如图，是四边形的边延长线上的一点，且，则下列条件中不能判定四边形是平行四边形的是（ ）
A．B．C．D．
23．下列命题错误的是（ ）
A．一组对边相等且一条对角线平分另一条对角线的四边形不一定是平行四边形
B．一组对角相等且这一组对角的顶点所连接的对角线平分另一条对角线的四边形不一定是平行四边形
C．一组对角相等且这一组对角的顶点连接的对角线被另一条对角线平分的四边形不一定是平行四边形
D．一组对边相等一组对角相等的四边形不一定是平行四边形
题型四 证明四边形是平行四边形
24．如图，已知在四边形中，，点F是的中点，连接交于点A，且点E是的中点，求证：四边形是平行四边形．
25．如图，已知在四边形中，，点是的中点，连接交于点，且点是的中点，求证：四边形是平行四边形．
26．已知，点B，D在线段AF上，，且．
(1)求证：；
(2)连接，，求证：四边形是平行四边形．
27．如图，在中，点，分别是，的中点，点是延长线上的一点，且，连接，，．
(1)求证：四边形是平行四边形；
(2)若，，，求四边形的面积．
28．如图，点A，F，C，D在同一直线上，AB＝DE，AF＝CD，BC＝EF．
(1)求证：∠ACB＝∠DFE；
(2)连接BF，CE，直接判断四边形BFEC的形状．
29．如图，中，D是边上任意一点，F是中点，过点C作∥交的延长线于点E，连接，．
(1)求证：四边形是平行四边形：
(2)若，，，求的长．
30．已知：如图，在四边形ABCD中，，对角线AC、BD相交于点O，且O是AC的中点．
(1)求证：≌；
(2)求证：四边形ABCD是平行四边形．
31．如图，在四边形中，点E，C为对角线上的两点，．连接．
(1)求证：四边形是平行四边形；
(2)若，求证：．
题型五 利用矩形的性质求角度和线段长度
32．如图，矩形 中，，交于点O，M，N分别为， 的中点，若，则的度数为（ ）
A．B．C．D．
33．如图，矩形中，于，且：：，则的度数为（ ）
A．B．C．D．
34．如图，矩形ABCD的顶点A，C分别在直线a，b上，且，，则的度数为（ ）
A．B．C．D．
35．如图，矩形的对角线，，则的长是（ ）
A．B．C．D．
36．如图，点为矩形对角线与的交点，若，则的长为（ ）
A．1B．2C．3D．6
37．如图，矩形的对角线交于点O，，则的长为（ ）
A．4B．6C．8D．
38．如图，在矩形中，对角线，相交于点，于点，于点．
（1）求证：．
（2）若，求的度数．
39．如图，在平行四边形中，于点，延长至点，使，连接，与交于点．
(1)求证：四边形为矩形；
(2)若，，，求的长．
40．如图，在矩形中，E是上一点，于点F，设．
(1)若，求证：；
(2)若，，且D、B、F在同一直线上时，求λ的值．
41．如图，在四边形中，，，，，分别为，的中点，连接，，延长交的延长线于点．
(1)求证：四边形为矩形；
(2)若，，求的长度．结果可保留根号
题型六 利用矩形的性质证明
42．如图，四边形是矩形，对角线相交于点，交的延长线于点．求证：．
43．如图，在矩形中， 点在边上，，，垂足为．试判断与的数量关系，并说明理由．
44．如图，在矩形ABCD中，点E，F分别在边AB，CD上，且AF＝CE，求证：DF＝BE．
45．如图，在平行四边形ABCD中，点M是AD边的中点，连接BM，CM，且BM＝CM．
(1)求证：四边形ABCD是矩形；
(2)若△BCM是直角三角形，写出AD与AB之间的数量关系，并证明．
46．在矩形ABCD中，E在BC的延长线上，连接DE，过点B作BF//DE交DA的延长线于点F．
(1)求证：BF＝DE；
(2)连接AE，若AF＝1，AB＝2，AD，求证：AE平分∠DEB．
47．如图，在矩形中，对角线、交于点，过点作，交的延长线于点．
(1)求证：；
(2)若，，求的周长．
题型七 证明四边形是矩形
48．如图，在平行四边形中，对角线、交于点，点为的中点，于点，点为上一点，连接，，且．
(1)求证：四边形为矩形；
(2)若，，，求的长．
49．如图，在平行四边形中，对角线相交于点O，且．
(1)求证：四边形是矩形；
(2)若，，求的长．
50．如图，中，为边的中点，连接并延长交的延长线于点，延长至点，使，连接、、．
(1)求证：；
(2)若，求证：四边形是矩形．
51．如图，已知在中，，
小明同学进行了以下操作：
第一步：作出的中点E；
第二步：连接并延长到D，使得；
第三步：连接和．
则四边形是什么特殊四边形？请说明理由．
52．如图，在平行四边形中，是对角线．
(1)用基本尺规作图完成以下作图，取边的点E，使得，并延长与的延长线交于点F，再连接；
(2)若，猜想四边形的形状，并说明理由．
题型八 利用菱形的性质求解
53．如图，菱形中，交于，于，连接，若，则的度数为（ ）
A．B．C．D．
54．如图，在菱形中，，分别在，上，且，与交于点，连接．若，则的度数为（ ）
A．B．C．D．
55．如图，在边长为2的菱形ABCD中，∠A=60°，点M是AD边的中点，点N是AB边上一动点，将AMN沿MN所在的直线翻折得到，连接，则线段长度的最小值是（ ）
A．－1B．－1C．－1D．2
56．如图，菱形中，E，F分别是，的中点．若菱形的周长为32，则线段的长为（ ）
A．4B．6C．8D．12
57．在菱形中，，，则菱形的周长为（ ）
A．48B．30C．20D．10
58．如图，在菱形中，，则菱形的周长是（ ）
A．B．C．D．
59．如图，菱形的对角线与相交于点O，过点O的直线分别交，于点E，F．若阴影部分的面积为5，则菱形的面积为（ ）
A．10B．15
C．20D．25
60．如图，已知菱形的两条对角线与长分别是和，则这个菱形的面积是（ ）
A．B．C．D．
61．如图，四边形 是菱形， 于点 ．若 ，，则 的长度为（ ）
A．B．C．D．
题型九 利用菱形的性质证明
62．下列说法正确的是（ ）
A．对角线相等的四边形是矩形
B．矩形的对角线相等且互相平分
C．对角线互相垂直的四边形是菱形
D．一组对边相等，另一组对边平行的四边形是平行四边形
63．下列命题中正确的是（ ）
A．菱形的对角线相等B．矩形的对角线互相垂直平分
C．对角线平分对角的平行四边形是菱形D．对角线相等的四边形是矩形
64．下列说法正确的是（ ）
A．矩形的对角线互相垂直B．矩形的邻边相等
C．菱形的对角线互相垂直平分D．菱形的对角线相等
65．以下条件中能判定平行四边形为菱形的是（ ）
A．B．C．D．
66．如图，在中，、分别为边、的中点，点、在上，且，若添加一个条件使四边形是菱形，则下列可以添加的条件是
A．B．C．D．
题型十 证明四边形是菱形
67．如图，菱形的对角线，相交于点O，E，F分别为边，的中点，连接，，.
(1)求证：四边形是菱形；
(2)如果，，求线段的长．
68．如图，在中，，D是的中点，过点作，且，连接．
(1)求证：四边形是菱形；
(2)若，，求菱形的面积．
69．如图，在矩形中，对角线交于点，分别过点作，的平行线交于点，连接交于点．
(1)求证：四边形是菱形；
(2)若，，求菱形的面积．
70．如图1，在中，，，是斜边上的中线，点E为射线上一点，将沿折叠，点B的对应点为点F．
(1)若，垂足为G，点F与点D在直线的异侧，连接．如图2，判断四边形的形状，并说明理由；
(2)若，，则的长度为____________．
71．如图，在中，点D是边的中点，点F，E分别是及其延长线上的点，，连接，．
(1)求证：四边形是平行四边形．
(2)当满足____________条件时，四边形为菱形．（填写序号）
①．②，③，④．
题型十一 利用正方形的性质求解
72．如图，在正方形中，为上一点，连接，交对角线于点，连接，若，则的度数为（ ）
A．B．C．D．
73．如图，在正方形中，对角线相交于点O．E、F分别为上一点，且，连接．若，则的度数为（ ）
A．B．C．D．
74．如图，边长为5的正方形中，点E、F分别在边、上，连接、、．已知平分，，则的长为（ ）
A．2B．4C．D．
75．如图，在正方形中，与相交于点，，点为上任意一点，于点，于点，则的值为（ ）
A．B．C．D．
76．如图，已知，相邻两条平行线间的距离都等于，如果正方形的四个顶点分别在四条直线上，与交于点，则正方形的面积为（ ）
A．B．C．D．
77．如图，点E在正方形ABCD的对角线AC上，且EC＝AE，Rt△FEG的两直角边EF，EG分别交BC，DC于点M，N．若正方形ABCD边长为4，则重叠部分四边形EMCN的面积为（ ）
A．2B．4C．6D．8
78．如图，将一张长方形纸对折，再对折，然后沿图中虚线剪下，剪下的图形展开后可得到（ ）
A．三角形B．梯形C．正方形D．五边形
79．如图，正方形ABCD中，AB=12，点E在边CD上，且BG=CG，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF，下列结论：①∠EAG＝45°：②CE＝3DE；③AG∥CF；④S△FGC=，其中正确结论的个数是 （ ）
A．1个B．2个C．3个D．4个
题型十二 利用正方形的性质证明
80．如图，在正方形中，将边绕点逆时针旋转至，连接，，若，，则线段的长为（ ）
A．B．C．D．
81．如图，已知正方形的边长为4，是对角线上一点，于点，于点，连接，．给出下列结论：①；②四边形的周长为8；③；④的最小值为2．其中正确结论有（ ）
A．1个B．2个C．3个D．4个
82．如图，在正方形中，点E、点F分别在上，且，若四边形的面积是，的长为1，则正方形的边长为（ ）
A．B．C．D．
83．如图，在正方形纸片中，对角线，交于点，折叠正方形纸片，使落在上，点恰好与上的点重合，展开后，折叠分别交，于，，连接，下列结论：①②③④四边形是菱形，正确的有（ ）
A．个B．个C．个D．个
84．已知：如图，，是正方形的对角线上的两点，且．那么四边形不具备的条件是（ ）
A．对角线相等B．四边相等C．对角线互相垂直D．对边平行
题型十三 证明四边形是正方形
85．在中，，点D是的中点，连接，过点B，C分别作，，、交于点F．
(1)求证：四边形是菱形；
(2)当和满足怎样的关系时，四边形是正方形？并证明你的结论．
86．如图，、是中的内、外角平分线，于，于，交的延长线于．
(1)判断四边形的形状，并说明理由．
(2)与相等吗？为什么？
(3)当满足______时，四边形是一个正方形？并给出证明．
87．在中，平分，于点，交于点，，连接.
(1)求证：；
(2)当满足什么条件时四边形是正方形？请说明理由.
88．如图，已知平行四边形ABCD中，对角线AC、BD交于点O，E是DB延长线上一点，若AE＝CE．
(1)求证：四边形ABCD是菱形；
(2)若∠BAO＝∠ABO，判断四边形ABCD的形状，并说明理由．
89．如图1，在矩形ABCD中，点E，F分别在AB，BC边上，DE＝AF，DE⊥AF于点G．
(1)求证：四边形ABCD是正方形；
(2)延长CB到点H，使得BH＝AE，判断△AHF的形状，并说明理由．
(3)如图2，在菱形ABCD中，点E，F分别在AB，BC边上，DE与AF相交于点G，DE＝AF，∠AED＝60°，AE＝6，BF＝2，请类比（2），求DE的长．