



所属成套资源:中考数学一轮复习知识点梳理+题型训练 (2份,原卷版+解析版)
中考数学一轮复习知识点梳理+题型训练专题17 相交线与平行线(2份,原卷版+解析版)
展开
这是一份中考数学一轮复习知识点梳理+题型训练专题17 相交线与平行线(2份,原卷版+解析版),文件包含中考数学一轮复习知识点梳理+题型训练专题17相交线与平行线原卷版doc、中考数学一轮复习知识点梳理+题型训练专题17相交线与平行线解析版doc等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。
【知识要点】
知识点一 垂线
直线的位置关系:在同一平面内,不重合的两条直线之间的位置关系只有两种:相交或平行。
垂线的概念:当两条相交直线所成的四个角中,有一个角是直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,交点叫做垂足。
【注意事项】线段与线段及射线与射线互相垂直,是指它们所在的直线互相垂直。
垂线的性质:1)在同一平面内,过一点有且只有一条直线与已知直线垂直。
2)两条直线互相垂直,则它们之间所形成的四个角为直角。
3)在同一平面内,如果一条直线垂直于两条平行线中的一条,那么这条直线垂直于另一条。垂线段最短定理:连接直线外一点与直线上各点的所有线段中,垂线段最短。
【注意事项】垂线是一条直线,而垂线段是一条线段。
点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
考查题型一 垂线定义的理解
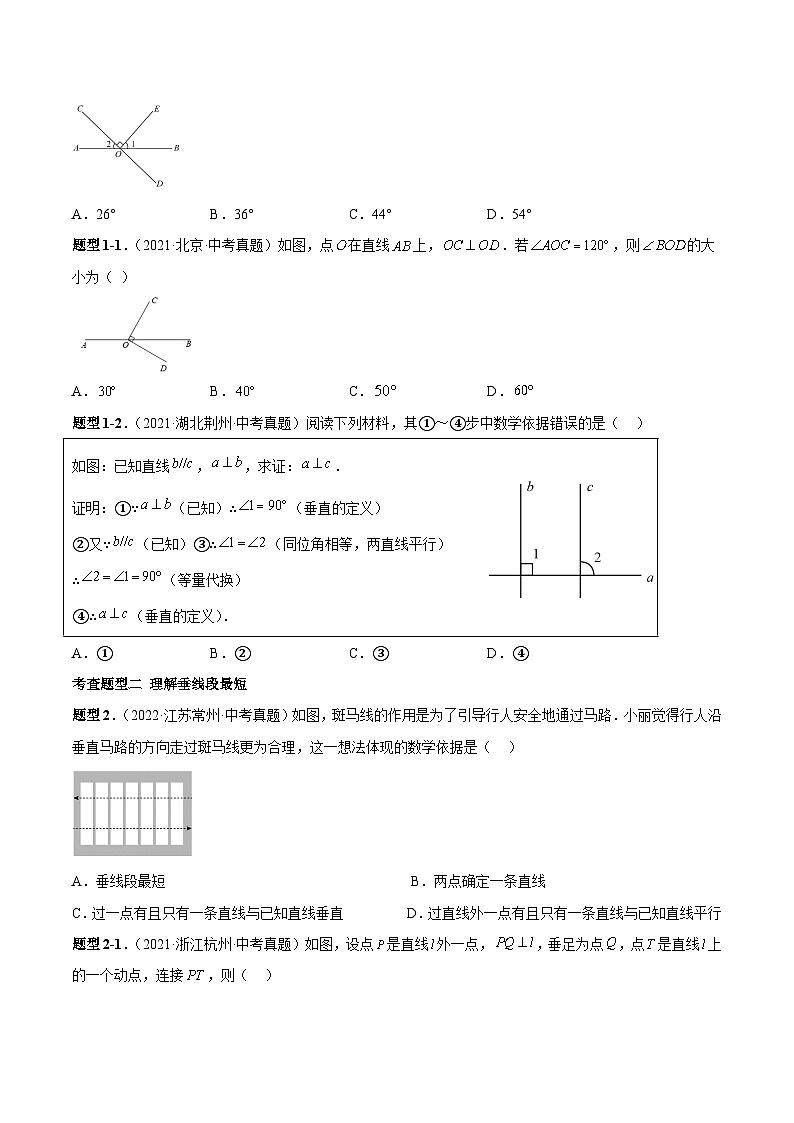
题型1.(2022·河南·中考真题)如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为( )
A.26°B.36°C.44°D.54°
题型1-1.(2021·北京·中考真题)如图,点在直线上,.若,则的大小为( )
A.B.C.D.
题型1-2.(2021·湖北荆州·中考真题)阅读下列材料,其①~④步中数学依据错误的是( )
A.①B.②C.③D.④
考查题型二 理解垂线段最短
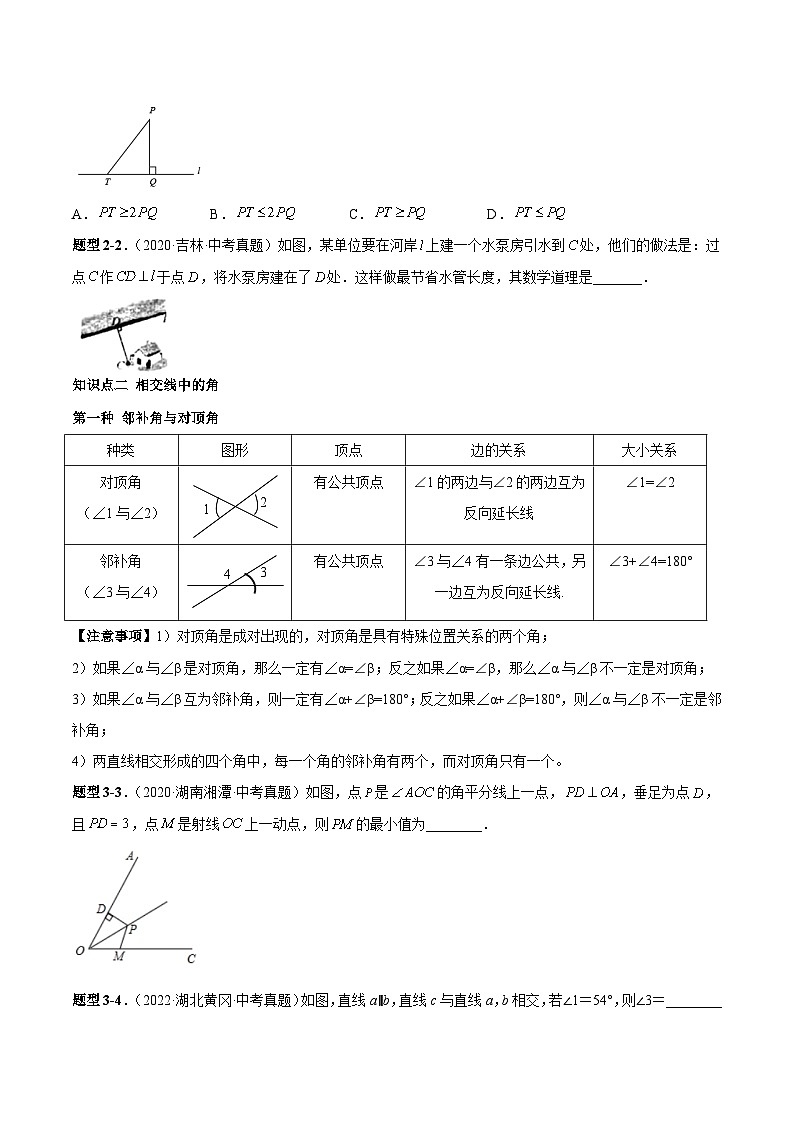
题型2.(2022·江苏常州·中考真题)如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )
A.垂线段最短 B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直 D.过直线外一点有且只有一条直线与已知直线平行
题型2-1.(2021·浙江杭州·中考真题)如图,设点是直线外一点,,垂足为点,点是直线上的一个动点,连接,则( )
A.B.C.D.
题型2-2.(2020·吉林·中考真题)如图,某单位要在河岸上建一个水泵房引水到处,他们的做法是:过点作于点,将水泵房建在了处.这样做最节省水管长度,其数学道理是_______.
知识点二 相交线中的角
第一种 邻补角与对顶角
【注意事项】1)对顶角是成对出现的,对顶角是具有特殊位置关系的两个角;
2)如果∠α与∠β是对顶角,那么一定有∠α=∠β;反之如果∠α=∠β,那么∠α与∠β不一定是对顶角;
3)如果∠α与∠β互为邻补角,则一定有∠α+∠β=180°;反之如果∠α+∠β=180°,则∠α与∠β不一定是邻补角;
4)两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个。
题型3-3.(2020·湖南湘潭·中考真题)如图,点是的角平分线上一点,,垂足为点,且,点是射线上一动点,则的最小值为________.
题型3-4.(2022·湖北黄冈·中考真题)如图,直线a∥b,直线c与直线a,b相交,若∠1=54°,则∠3=________度.
考查题型四 利用邻补角互补求角度
题型4.(2022·湖南娄底·中考真题)一条古称在称物时的状态如图所示,已知,则( )
A.B.C.D.
题型4-1.(2021·河南·中考真题)如图,,,则的度数为( )
A.B.C.D.
题型4-2.(2021·湖南湘潭·中考真题)如图,直线a,b被直线c所截,已知,,则为______度.
第二种 同位角、内错角与同旁内角
同位角:两条直线被第三条直线所截,在截线的同旁,在被截两条直线同侧,具有这样位置关系的一对角叫做内错角。(同旁同侧)如:∠1和∠5。
内错角:两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角。(内部异侧)如:∠3和∠5。
同旁内角:两条直线被第三条直线所截,在截线的同旁,在被截两条直线内部,具有这样位置关系的一对叫同旁内角。(同旁内侧)如:∠3和∠6。
三线八角的概念:指的是两条直线被第三条直线所截而形成的八个角,其中同位角4对,内错角有2对,同旁内角有2对。
【速记同位角、内错角与同旁内角】
考查题型五 同位角、内错角、同旁内角的识别
题型5.(2022·青海·中考真题)数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示( )
A.同旁内角、同位角、内错角
B.同位角、内错角、对顶角
C.对顶角、同位角、同旁内角
D.同位角、内错角、同旁内角
题型5-1.(2022·广西贺州·中考真题)如图,直线a,b被直线c所截,下列各组角是同位角的是( )
A.与B.与C.与D.与
题型5-2.(2021·广西贺州·中考真题)如图,下列两个角是同旁内角的是( )
A.与B.与C.与D.与
题型5-3.(2021·广西百色·中考真题)如图,与∠1是内错角的是( )
A.∠2B.∠3C.∠4D.∠5
知识点三 平行线
平行线的定义:在同一平面内,不相交的两条直线叫做平行线,平行用符号“∥”表示,
如:直线a与直线互相平行,记作a∥,读作a平行于b。
判断同一平面内两直线的位置关系时,可以根据它们的公共点的个数来确定:
①有且只有一个公共点,两直线相交;
②无公共点,则两直线平行;
③两个或两个以上公共点,则两直线重合
平行公理(唯一性):经过直线外一点,有且只有一条直线与这条直线平行。
平行公理的推论(传递性):如果两条直线都与第三条直线平行,那么这两条直线也互相平行
a
几何描述 :∵∥a,∥a
∴∥
平行线的性质:
性质1:两直线平行,同位角相等;
几何符号语言:∵AB∥CD
∴∠3=∠2(两直线平行,同位角相等)
A
B
C
D
E
F
1
2
3
4
性质2:两直线平行,内错角相等;
几何符号语言:∵AB∥CD
∴∠1=∠2(两直线平行,内错角相等)
性质3:两直线平行,同旁内角互补.。
几何符号语言:∵AB∥CD
∴∠4+∠2=180°(两直线平行,同旁内角互补)
平行线的判定
判定方法1 :两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行
简称:同位角相等,两直线平行
几何符号语言:∵∠3=∠2∴AB∥CD(同位角相等,两直线平行)
判定方法2 :两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行
简称:内错角相等,两直线平行
几何符号语言:∵∠1=∠2∴AB∥CD(内错角相等,两直线平行)
判定方法3: 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行
简称:同旁内角互补,两直线平行
几何符号语言:∵∠4+∠2=180°∴AB∥CD(同旁内角互补,两直线平行)
考查题型三 理解对顶角的性质
题型3.(2022·北京·中考真题)如图,利用工具测量角,则的大小为( )
A.30°B.60°C.120°D.150°
题型3-1.(2022·江苏苏州·中考真题)如图,直线AB与CD相交于点O,,,则的度数是( )
A.25°B.30°C.40°D.50°
题型3-2.(2022·陕西·中考真题)如图,.若,则的大小为( )
A.B.C.D.
考查题型六 利用同位角判定平行线
题型6.(2022·浙江台州·中考真题)如图,已知,为保证两条铁轨平行,添加的下列条件中,正确的是( )
A.B.C.D.
题型6-1.(2022·吉林·中考真题)如图,如果,那么,其依据可以简单说成( )
A.两直线平行,内错角相等B.内错角相等,两直线平行
C.两直线平行,同位角相等D.同位角相等,两直线平行
题型6-2.(2021·江苏泰州·中考真题)如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转 ___°.
考查题型七 利用内错角判定平行线
题型7.(2022·新疆·中考真题)如图.AB与CD相交于点O,若,则( )
A.B.C.D.
题型7-1.(2021·甘肃兰州·中考真题)将一副三角板如图摆放,则______∥______,理由是______.
考查题型八 利用同旁内角判定平行线
题型8.(2022·湖南郴州·中考真题)如图,直线,且直线a,b被直线c,d所截,则下列条件不能判定直线的是( )
A.B.C.D.
题型8-1.(2020·湖南郴州·中考真题)如图,直线被直线所截,下列条件能判定的是( )
A.B.
C.D.
考查题型九 利用平行线的性质求解
题型9.(2022·广东·中考真题)如图,直线a,b被直线c所截,a∥b,∠1=40°,则∠2等于( )
A.30°B.40°C.50°D.60°
题型9-1.(2022·云南·中考真题)如图,已知直线c与直线a、b都相交.若ab,∠1=85°,则∠2=( )
A.110°B.105°C.100°D.95°
题型9-2.(2022·江苏盐城·中考真题)小明将一块直角三角板摆放在直尺上,如图所示,则与的关系是( )
A.互余B.互补C.同位角D.同旁内角
题型9-3.(2022·内蒙古内蒙古·中考真题)如图,直线,截线c,d相交成30°角,,则的度数是( )
A.B.C.D.
题型9-4.(2022·浙江杭州·中考真题)如图,已知,点E在线段AD上(不与点A,点D重合),连接CE.若∠C=20°,∠AEC=50°,则∠A=( )
A.10°B.20°C.30°D.40°
题型9-5.(2022·浙江绍兴·中考真题)如图,把一块三角板的直角顶点B放在直线上,,ACEF,则( )
A.30°B.45°
C.60°D.75°
题型9-6.(2022·黑龙江齐齐哈尔·中考真题)如图所示,直线a∥b,点A在直线a上,点B在直线b上,AC=BC,∠C=120°,∠1=43°,则∠2的度数为( )
A.57°B.63°
C.67°D.73°
题型9-7.(2022·重庆·中考真题)如图,直线,被直线所截,,,则的度数为( )
A.B.C.D.
题型9-8.(2022·山东滨州·中考真题)如图,在弯形管道中,若,拐角,则的大小为( )
A.B.C.D.
题型9-9.(2022·山东济宁·中考真题)如图,直线l1,l2,l3被直线l4所截,若l1l2,l2l3,∠1=126°32',则∠2的度数是___________.
考查题型十 平行线性质的实际应用
题型10.(2022·湖南长沙·中考真题)如图,,则的度数为( )
A.B.C.D.
题型10-1.(2022·湖北恩施·中考真题)已知直线,将含30°角的直角三角板按图所示摆放.若,则( )
A.120°B.130°C.140°D.150°
题型10-2.(2022·内蒙古通辽·中考真题)如图,一束光线先后经平面镜,反射后,反射光线与平行,当时,的度数为( )
A.B.C.D.
题型10-3.(2022·浙江金华·中考真题)图1是光伏发电场景,其示意图如图2,为吸热塔,在地平线上的点B,处各安装定日镜(介绍见图3).绕各中心点旋转镜面,使过中心点的太阳光线经镜面反射后到达吸热器点F处.已知,在点A观测点F的仰角为.
(1)点F的高度为______m.
(2)设,则与的数量关系是_______.
如图:已知直线,,求证:.
证明:①∵(已知)∴(垂直的定义)
②又∵(已知)③∴(同位角相等,两直线平行)
∴(等量代换)
④∴(垂直的定义).
种类
图形
顶点
边的关系
大小关系
对顶角
(∠1与∠2)
1
2
有公共顶点
∠1的两边与∠2的两边互为反向延长线
∠1=∠2
邻补角
(∠3与∠4)
4
3
有公共顶点
∠3与∠4有一条边公共,另一边互为反向延长线.
∠3+∠4=180°
相关试卷
这是一份中考数学一轮复习知识点梳理+题型训练专题38 概率(2份,原卷版+解析版),文件包含中考数学一轮复习知识点梳理+题型训练专题38概率原卷版doc、中考数学一轮复习知识点梳理+题型训练专题38概率解析版doc等2份试卷配套教学资源,其中试卷共44页, 欢迎下载使用。
这是一份中考数学一轮复习知识点梳理+题型训练专题33 图形的相似(2份,原卷版+解析版),文件包含中考数学一轮复习知识点梳理+题型训练专题33图形的相似原卷版doc、中考数学一轮复习知识点梳理+题型训练专题33图形的相似解析版doc等2份试卷配套教学资源,其中试卷共91页, 欢迎下载使用。
这是一份中考数学一轮复习知识点梳理+题型训练专题31 平移与旋转(2份,原卷版+解析版),文件包含中考数学一轮复习知识点梳理+题型训练专题31平移与旋转原卷版doc、中考数学一轮复习知识点梳理+题型训练专题31平移与旋转解析版doc等2份试卷配套教学资源,其中试卷共79页, 欢迎下载使用。








