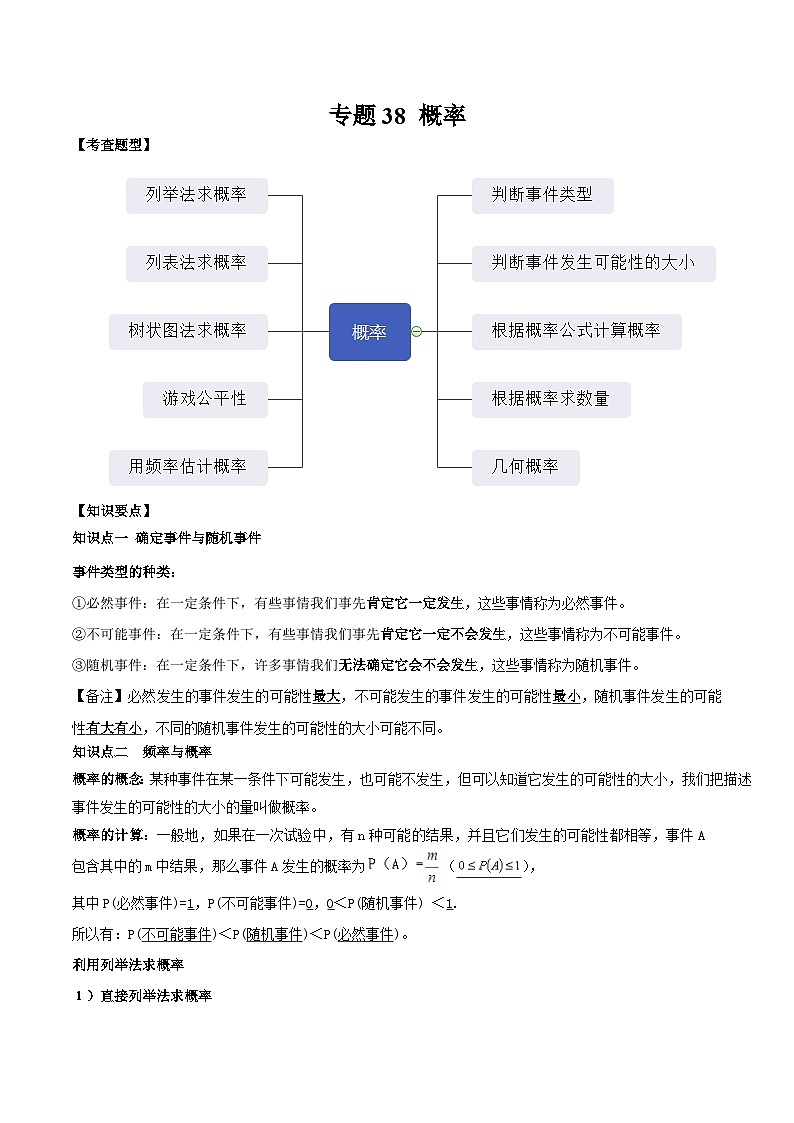


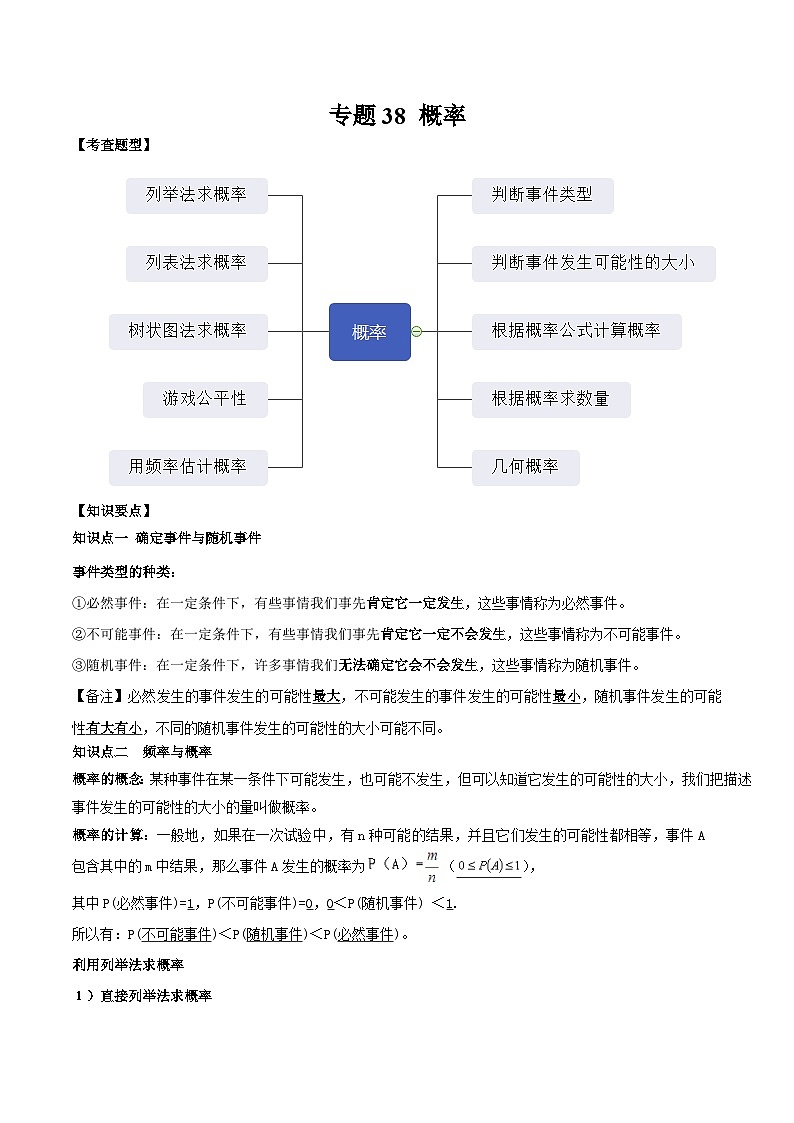


所属成套资源:中考数学一轮复习知识点梳理+题型训练 (2份,原卷版+解析版)
中考数学一轮复习知识点梳理+题型训练专题38 概率(2份,原卷版+解析版)
展开
这是一份中考数学一轮复习知识点梳理+题型训练专题38 概率(2份,原卷版+解析版),文件包含中考数学一轮复习知识点梳理+题型训练专题38概率原卷版doc、中考数学一轮复习知识点梳理+题型训练专题38概率解析版doc等2份试卷配套教学资源,其中试卷共44页, 欢迎下载使用。
【知识要点】
知识点一 确定事件与随机事件
事件类型的种类:
①必然事件:在一定条件下,有些事情我们事先肯定它一定发生,这些事情称为必然事件。
②不可能事件:在一定条件下,有些事情我们事先肯定它一定不会发生,这些事情称为不可能事件。
③随机事件:在一定条件下,许多事情我们无法确定它会不会发生,这些事情称为随机事件。
【备注】必然发生的事件发生的可能性最大,不可能发生的事件发生的可能性最小,随机事件发生的可能性有大有小,不同的随机事件发生的可能性的大小可能不同。
知识点二 频率与概率
概率的概念:某种事件在某一条件下可能发生,也可能不发生,但可以知道它发生的可能性的大小,我们把描述事件发生的可能性的大小的量叫做概率。
概率的计算:一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为(),
其中P(必然事件)=1,P(不可能事件)=0,0<P(随机事件) <1.
所以有:P(不可能事件)<P(随机事件)<P(必然事件)。
利用列举法求概率
1)直接列举法求概率
当一次试验中,可能出现的结果是有限个,并且各种结果发生的可能性相等时,通常采用直接列举法。
2)列表法求概率
当一次试验要设计两个因素, 并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法。
3)树状图法求概率
当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率。
利用频率估计概率
实际上,我们可以通过大量的重复试验,用一个随机事件发生的频率去估计它的概率。用频率估计概率 ,虽然不像列举法能确切地计算出随机事件的概率,但由于不受“各种结果出现的可能性相等”的条件限制,使得可求概率的随机事件的范围扩大。
通常,在多次重复实验中,一个随机事件发生的频率会在某一个常数附近摆动,并且随着试验次数增多,摆动的幅度会减小,这个性质称为频率的稳定性.
【注意事项】概率是频率的稳定值,而频率是概率的近似值。
考查题型一 判断事件类型
典例1(2022·湖北武汉·统考中考真题)彩民李大叔购买1张彩票,中奖.这个事件是( )
A.必然事件B.确定性事件C.不可能事件D.随机事件
变式1-1.(2022·江苏扬州·统考中考真题)下列成语所描述的事件属于不可能事件的是( )
A.水落石出B.水涨船高C.水滴石穿D.水中捞月
变式1-2(2022·四川德阳·统考中考真题)下列事件中,属于必然事件的是( )
A.抛掷硬币时,正面朝上
B.明天太阳从东方升起
C.经过红绿灯路口,遇到红灯
D.玩“石头、剪刀、布”游戏时,对方出“剪刀”
变式1-3(2022·江西·统考中考真题)某医院计划选派护士支援某地的防疫工作,甲、乙、丙、丁4名护士积极报名参加,其中甲是共青团员,其余3人均是共产党员.医院决定用随机抽取的方式确定人选.
(1)“随机抽取1人,甲恰好被抽中”是__________事件;
A.不可能 B.必然 C.随机
(2)若需从这4名护士中随机抽取2人,请用画树状图法或列表法求出被抽到的两名护士都是共产党员的概率.
考查题型二 判断事件发生可能性的大小
典例2(2022·江苏泰州·统考中考真题)如图,一张圆桌共有3个座位,甲、乙,丙3人随机坐到这3个座位上,则甲和乙相邻的概率为( )
A.B.C.D.
变式2-1(2021·贵州黔东南·统考中考真题)一只不透明的袋子中装有3个黑球和2个白球,这些除颜色外无其他差别,从中任意摸出3个球,下列事件是确定事件的为( )
A.至少有1个球是黑球B.至少有1个球是白球
C.至少有2个球是黑球D.至少有2个球是白球
变式2-2.(2022·贵州贵阳·统考中考真题)某校九年级选出三名同学参加学校组织的“法治和安全知识竞赛”.比赛规定,以抽签方式决定每个人的出场顺序,主持人将表示出场顺序的数字1,2,3分别写在3张同样的纸条上,并将这些纸条放在一个不透明的盒子中,搅匀后从中任意抽出一张,小星第一个抽,下列说法中正确的是( )
A.小星抽到数字1的可能性最小B.小星抽到数字2的可能性最大
C.小星抽到数字3的可能性最大D.小星抽到每个数的可能性相同
考查题型三 根据概率公式计算概率
典例3(2022·广东·统考中考真题)书架上有2本数学书、1本物理书.从中任取1本书是物理书的概率为( )
A.B.C.D.
变式3-1(2022·湖南怀化·统考中考真题)从下列一组数﹣2,π,﹣,﹣0.12,0,﹣中随机抽取一个数,这个数是负数的概率为( )
A.B.C.D.
变式3-2(2022·内蒙古呼和浩特·统考中考真题)不透明袋中装有除颜色外完全相同的个白球、个红球,则任意摸出一个球是红球的概率是( )
A.B.C.D.
变式3-3(2022·甘肃兰州·统考中考真题)无色酚酞溶液是一中常见常用酸碱指示剂,广泛应用于检验溶液酸碱性,通常情况下酚酞溶液遇酸溶液不变色,遇中性溶液也不变色,遇碱溶液变红色.现有5瓶缺失标签的无色液体:蒸馏水、白醋溶液、食用碱溶液、柠檬水溶液、火碱溶液,将酚酞试剂滴入任意一瓶液体后呈现红色的概率是( )
A.B.C.D.
变式3-4(2022·山东东营·统考中考真题)如图,任意将图中的某一白色方块涂黑后,能使所有黑色方块构成的图形是轴对称图形的概率是( )
A.B.C.D.
考查题型四 根据概率求数量
典例4(2022·黑龙江绥化·统考中考真题)一个不透明的箱子中有5个红球和若干个黄球,除颜色外无其它差别.若任意摸出一个球,摸出红球的概率为,则这个箱子中黄球的个数为______个.
变式4-1(2022·辽宁鞍山·统考中考真题)一个不透明的口袋中装有5个红球和个黄球,这些球除颜色外都相同,某同学进行了如下试验:从袋中随机摸出1个球记下它的颜色后,放回摇匀,为一次摸球试验.根据记录在下表中的摸球试验数据,可以估计出的值为_________.
变式4-2(2022·四川广元·统考中考真题)一个袋中装有m个红球,10个黄球,n个白球,每个球除颜色外都相同,任意摸出一个球,摸到黄球的概率与不是黄球的概率相同,那么m与n的关系是________.
考查题型五 几何概率
典例5(2022·江苏苏州·统考中考真题)如图,在的长方形网格飞镖游戏板中,每块小正方形除颜色外都相同,小正方形的顶点称为格点,扇形OAB的圆心及弧的两端均为格点.假设飞镖击中每一块小正方形是等可能的(击中扇形的边界或没有击中游戏板,则重投1次),任意投掷飞镖1次,飞镖击中扇形OAB(阴影部分)的概率是( )
A.B.C.D.
变式5-1(2022·辽宁朝阳·统考中考真题)如图所示的是由8个全等的小正方形组成的图案,假设可以随意在图中取一点,那么这个点取在阴影部分的概率是( )
A.B.C.D.1
变式5-2(2022·江苏徐州·统考中考真题)将一枚飞镖任意投掷到如图所示的正六边形镖盘上,若飞镖落在镖盘上各点的机会相等,则飞镖落在阴影区域的概率为( )
A.B.C.D.
变式5-3(2021·江苏常州·统考中考真题)以下转盘分别被分成2个、4个、5个、6个面积相等的扇形,任意转动这4个转盘各1次.已知某转盘停止转动时,指针落在阴影区域的概率是,则对应的转盘是( )
A.B.C.D.
变式5-4(2021·甘肃兰州·统考中考真题)如图,将一个棱长为3的正方体表面涂上颜色,再把它分割成棱长为1的小正方体,将它们全部放入一个不透明盒子中摇匀,随机取出一个小正方体,只有一个面被涂色的概率为( )
A.B.C.D.
变式5-5(2022·四川成都·统考中考真题)如图,已知⊙是小正方形的外接圆,是大正方形的内切圆.现假设可以随意在图中取点,则这个点取在阴影部分的概率是_________.
考查题型六 列举法求概率
典例6(2022·安徽·统考中考真题)随着信息化的发展,二维码已经走进我们的日常生活,其图案主要由黑、白两种小正方形组成.现对由三个小正方形组成的“”进行涂色,每个小正方形随机涂成黑色或白色,恰好是两个黑色小正方形和一个白色小正方形的概率为( )
A.B.C.D.
变式6-1(2022·广西贵港·中考真题)从,,2这三个数中任取两个不同的数,作为点的坐标,则该点落在第三象限的概率是___.
考查题型七 列表法求概率
典例7(2022·山西·中考真题)“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界普为“中国第五大发明”,小文购买了“二十四节气”主题邮票,他要将“立春”“立夏”“秋分”“大暑”四张邮票中的两张送给好朋友小乐.小文将它们背面朝上放在桌面上(邮票背面完全相同),让小乐从中随机抽取一张(不放回),再从中随机抽取一张,则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是( )
A.B.C.D.
变式7-1(2022·山东临沂·统考中考真题)为做好疫情防控工作,某学校门口设置了,两条体温快速检测通道,该校同学王明和李强均从通道入校的概率是( )
A.B.C.D.
变式7-2(2022·辽宁朝阳·统考中考真题)某社区组织A,B,C,D四个小区的居民进行核酸检测,有很多志愿者参与此项检测工作,志愿者王明和李丽分别被随机安排到这四个小区中的一个小区组织居民排队等候.
(1)王明被安排到A小区进行服务的概率是 .
(2)请用列表法或画树状图法求出王明和李丽被安排到同一个小区工作的概率.
变式7-3(2022·江苏宿迁·统考中考真题)从甲、乙、丙、丁4名学生中选2名学生参加一次乒乓球单打比赛,求下列事件发生的概率.
(1)甲一定参加比赛,再从其余3名学生中任意选取1名,恰好选中丙的概率是 ;
(2)任意选取2名学生参加比赛,求一定有乙的概率.(用树状图或列表的方法求解).
变式7-4(2022·山东青岛·统考中考真题)2022年3月23日下午,“天宫课堂”第二课开讲,航天员翟志刚、王亚平、叶光富相互配合进行授课,激发了同学们学习航天知识的热情.小冰和小雪参加航天知识竞赛时,均获得了一等奖,学校想请一位同学作为代表分享获奖心得.小冰和小雪都想分享,于是两人决定一起做游戏,谁获胜谁分享,游戏规则如下:甲口袋装有编号为1,2的两个球,乙口袋装有编号为1,2,3,4,5的五个球,两口袋中的球除编号外都相同.小冰先从甲口袋中随机摸出一个球,小雪再从乙口袋中随机摸出一个球,若两球编号之和为奇数,则小冰获胜;若两球编号之和为偶数,则小雪获胜.
请用列表或画树状图的方法,说明这个游戏对双方是否公平.
考查题型八 树状图法求概率
典例8(2022·北京·统考中考真题)不透明的袋子中装有红、绿小球各一个,除颜色外两个小球无其他差别,从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,那么第一次摸到红球、第二次摸到绿球的概率是( )
A.B.C.D.
变式8-1(2022·湖北武汉·统考中考真题)班长邀请,,,四位同学参加圆桌会议.如图,班长坐在⑤号座位,四位同学随机坐在①②③④四个座位,则,两位同学座位相邻的概率是( )
A.B.C.D.
变式8-2(2022·山东烟台·统考中考真题)如图所示的电路图,同时闭合两个开关能形成闭合电路的概率是( )
A.B.C.D.1
变式8-3(2022·江苏淮安·统考中考真题)一只不透明的袋子中装有3个大小、质地完全相同的乒乓球,球面上分别标有数字1、2、3,搅匀后先从袋子中任意摸出1个球,记下数字后放回,搅匀后再从袋子中任意摸出1个球,记下数字.
(1)第一次摸到标有偶数的乒乓球的概率是______;
(2)用画树状图或列表等方法求两次都摸到标有奇数的乒乓球的概率.
变式8-4(2022·江苏连云港·统考中考真题)“石头、剪子、布”是一个广为流传的游戏,规则是:甲、乙两人都做出“石头”“剪子”“布”3种手势中的1种,其中“石头”赢“剪子”,“剪子”赢“布”,“布”赢“石头”,手势相同不分输赢.假设甲、乙两人每次都随意并且同时做出3种手势中的1种.
(1)甲每次做出“石头”手势的概率为_________;
(2)用画树状图或列表的方法,求乙不输的概率.
考查题型九 游戏公平性
典例9(2021·山东青岛·统考中考真题)为践行青岛市中小学生“十个一”行动,某校举行文艺表演,小静和小丽想合唱一首歌.小静想唱《红旗飘飘》,而小丽想唱《大海啊,故乡》.她们想通过做游戏的方式来决定合唱哪一首歌,于是一起设计了一个游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.同时转动两个转盘,若两个指针指向的数字之积小于4,则合唱《大海啊,故乡》,否则合唱《红旗飘飘》;若指针刚好落在分割线上,则需要重新转动转盘.请用列表或画树状图的方法说明这个游戏是否公平.
变式9-1(2021·贵州遵义·统考中考真题)现有A,B两个不透明的袋子,A袋的4个小球分别标有数字1,2,3,4;B袋的3个小球分别标有数字1,2,3.(每个袋中的小球除数字外,其它完全相同.)
(1)从A,B两个袋中各随机摸出一个小球,则两个小球上数字相同的概率是 ;
(2)甲、乙两人玩摸球游戏,规则是:甲从A袋中随机摸出一个小球,乙从B袋中随机摸出一个小球,若甲、乙两人摸到小球的数字之和为奇数时,则甲胜;否则乙胜,用列表或树状图的方法说明这个规则对甲、乙两人是否公平.
变式9-(2021·辽宁丹东·统考中考真题)一个不透明的袋子中装有4个只有颜色不同的小球,其中2个红球,2个白球,摇匀后从中一次性摸出两个小球.
(1)请用列表格或画树状图的方法列出所有可能性;
(2)若摸到两个小球的颜色相同,甲获胜;摸到两个小球颜色不同,乙获胜.这个游戏对甲、乙双方公平吗?请说明理由.
考查题型十 用频率估计概率
典例10(2021·四川乐山·统考中考真题)在一次心理健康教育活动中,张老师随机抽取了40名学生进行了心理健康测试,并将测试结果按“健康、亚健康、不健康”绘制成下列表格,其中测试结果为“健康”的频率是( ).
A.32B.7C.D.
变式10-1(2021·山东青岛·统考中考真题)在一个不透明的袋中装有若干个红球和4个黑球,每个球除颜色外完全相同.摇匀后从中摸出一个球,记下颜色后再放回袋中.不断重复这一过程,共摸球100次.其中有40次摸到黑球,估计袋中红球的个数是__________.
变式10-2(2021·湖北宜昌·统考中考真题)社团课上,同学们进行了“摸球游戏”:在一个不透明的盒子里装有几十个除颜色不同外其余均相同的黑、白两种球,将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.整理数据后,制作了“摸出黑球的频率”与“摸球的总次数”的关系图象如图所示,经分析可以推断盒子里个数比较多的是___________(填“黑球”或“白球”).
变式10-3(2021·辽宁锦州·统考中考真题)一个口袋中有红球、白球共20个,这些球除颜色外都相同,将口袋中的球搅匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了300次球,发现有120次摸到红球,则这个口袋中红球的个数约为____.
变式10-4(2021·湖南长沙·统考中考真题)“网红”长沙入选2021年“五一”假期热门旅游城市.本市某景点为吸引游客,设置了一种游戏,其规则如下:凡参与游戏的游客从一个装有12个红球和若干个白球(每个球除颜色外,其他都相同)的不透明纸箱中,随机摸出一个球,摸到红球就可免费得到一个景点吉祥物.据统计参与这种游戏的游客共有60000人,景点一共为参与该游戏的游客免费发放了景点吉祥物15000个.
(1)求参与该游戏可免费得到景点吉祥物的频率;
(2)请你估计纸箱中白球的数量接近多少?
变式10-5(2021·甘肃武威·统考中考真题)一个不透明的箱子里装有3个红色小球和若干个白色小球,每个小球除颜色外其他完全相同,每次把箱子里的小球摇匀后随机摸出一个小球,记下颜色后再放回箱子里,通过大量重复实验后,发现摸到红色小球的频率稳定于0.75左右.
(1)请你估计箱子里白色小球的个数;
(2)现从该箱子里摸出1个小球,记下颜色后放回箱子里,摇匀后,再摸出1个小球,求两次摸出的小球颜色恰好不同的概率(用画树状图或列表的方法).
变式10-6(2021·湖南岳阳·统考中考真题)国务院教育督导委员会办公室印发的《关于组织责任督学进行“五项管理”督导的通知》指出,要加强中小学生作业、睡眠、手机、读物、体质管理.某校数学社团成员采用随机抽样的方法,抽取了八年级部分学生,对他们一周内平均每天的睡眠时间(单位:)进行了调查,将数据整理后得到下列不完整的统计图表:
请根据图表信息回答下列问题:
(1)频数分布表中,________,________;
(2)扇形统计图中,组所在扇形的圆心角的度数是________;
(3)请估算该校600名八年级学生中睡眠不足7小时的人数;
(4)研究表明,初中生每天睡眠时长低于7小时,会严重影响学习效率.请你根据以上调查统计结果,向学校提出一条合理化的建议.
摸球的总次数
100
500
1000
2000
…
摸出红球的次数
19
101
199
400
…
摸出红球的频率
0.190
0.202
0.199
0.200
…
类型
健康
亚健康
不健康
数据(人)
32
7
1
组别
睡眠时间分组
频数
频率
4
0.08
8
0.16
10
21
0.42
0.14
相关试卷
这是一份中考数学一轮复习知识点梳理+题型训练专题33 图形的相似(2份,原卷版+解析版),文件包含中考数学一轮复习知识点梳理+题型训练专题33图形的相似原卷版doc、中考数学一轮复习知识点梳理+题型训练专题33图形的相似解析版doc等2份试卷配套教学资源,其中试卷共91页, 欢迎下载使用。
这是一份中考数学一轮复习知识点梳理+题型训练专题28 圆(2份,原卷版+解析版),文件包含中考数学一轮复习知识点梳理+题型训练专题28圆原卷版doc、中考数学一轮复习知识点梳理+题型训练专题28圆解析版doc等2份试卷配套教学资源,其中试卷共75页, 欢迎下载使用。
这是一份中考数学一轮复习知识点梳理+题型训练专题21 勾股定理(2份,原卷版+解析版),文件包含中考数学一轮复习知识点梳理+题型训练专题21勾股定理原卷版doc、中考数学一轮复习知识点梳理+题型训练专题21勾股定理解析版doc等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。









