中考数学一轮复习知识梳理+考点精讲专题11 反比例函数的图像与性质（2份，原卷版+解析版）

这是一份中考数学一轮复习知识梳理+考点精讲专题11 反比例函数的图像与性质（2份，原卷版+解析版），文件包含中考数学一轮复习知识梳理+考点精讲专题11反比例函数的图像与性质原卷版doc、中考数学一轮复习知识梳理+考点精讲专题11反比例函数的图像与性质解析版doc等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。

反比例函数是中考命题热点之一，主要考察反比例函数的图象、性质及解析式确实定，也经常与一次函数、二次函数及几何图形等知识综合考察.考察形式以选择题、填空题为主.
考标要求
1.理解反比例函数的概念，能根据条件确定反比例函数的解析式.
2.会画反比例函数图象，根据图象和解析式探究并理解其根本性质.
考点精讲
3.能用反比例函数解决简单实际问题.
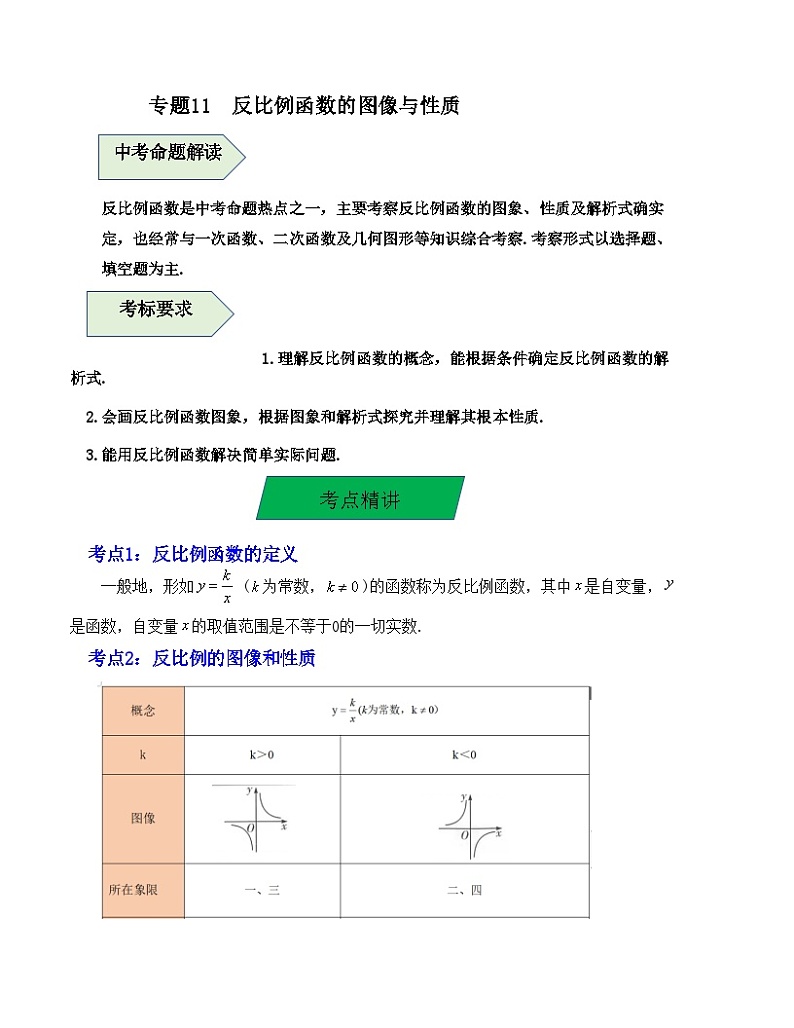
考点1：反比例函数的定义
一般地，形如 (为常数，)的函数称为反比例函数，其中是自变量，是函数，自变量的取值范围是不等于0的一切实数.
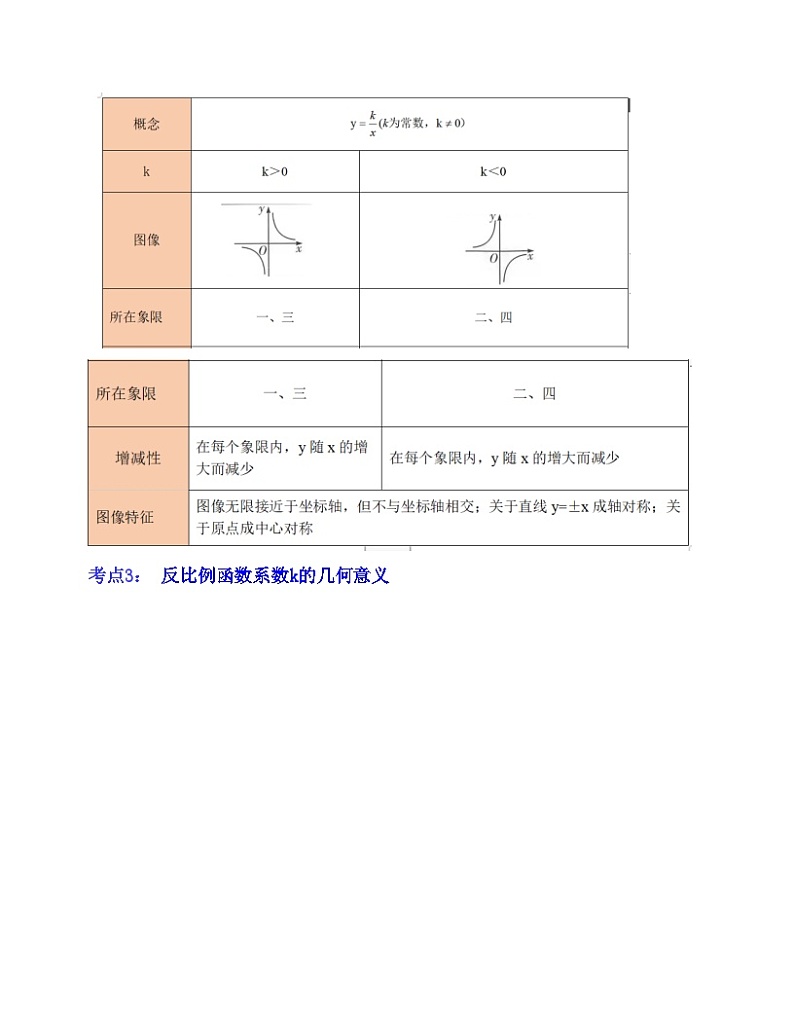
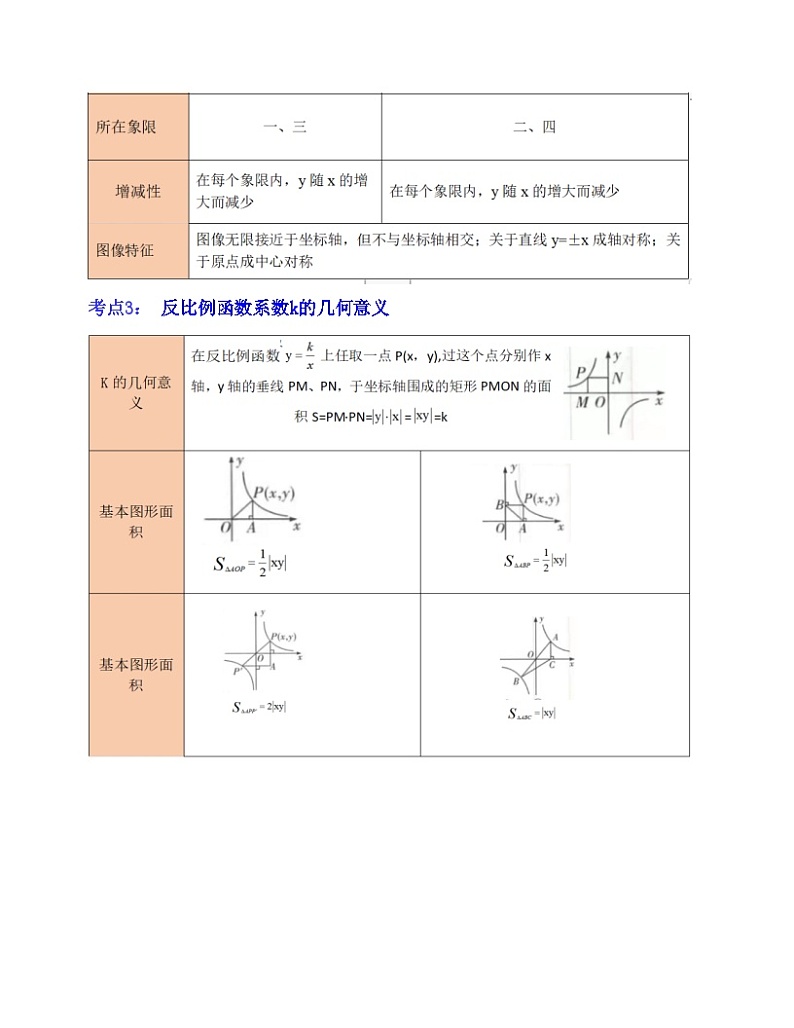
考点2：反比例的图像和性质

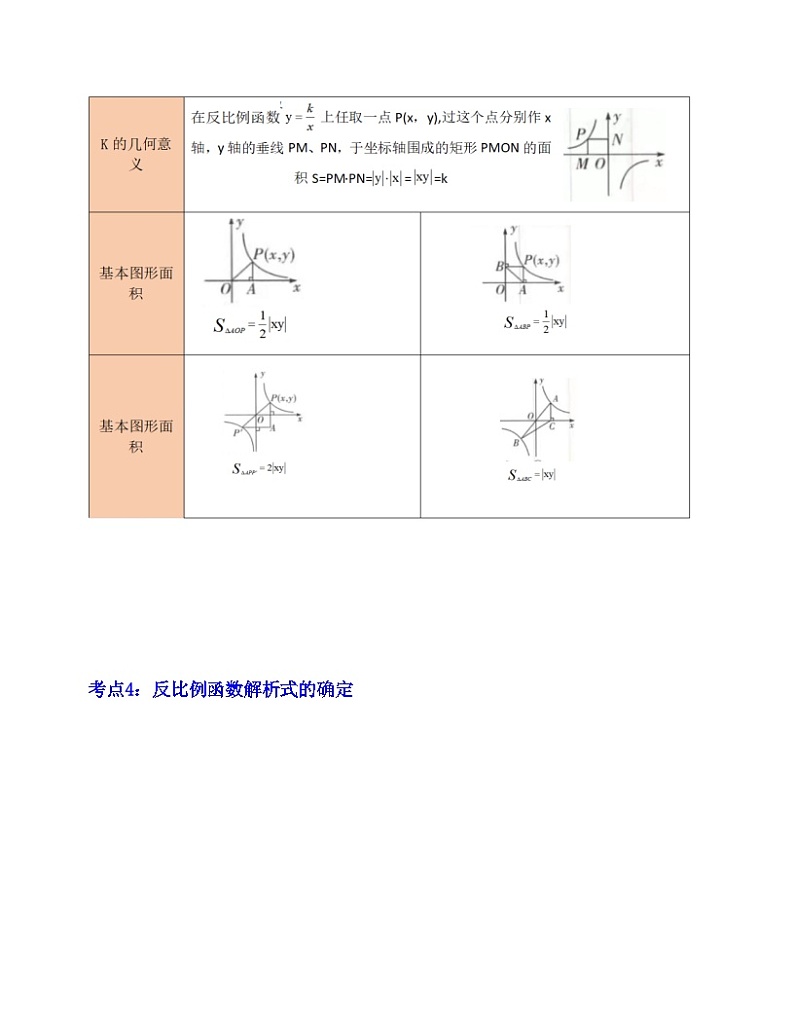
考点3： 反比例函数系数k的几何意义
考点4：反比例函数解析式的确定
母题精讲
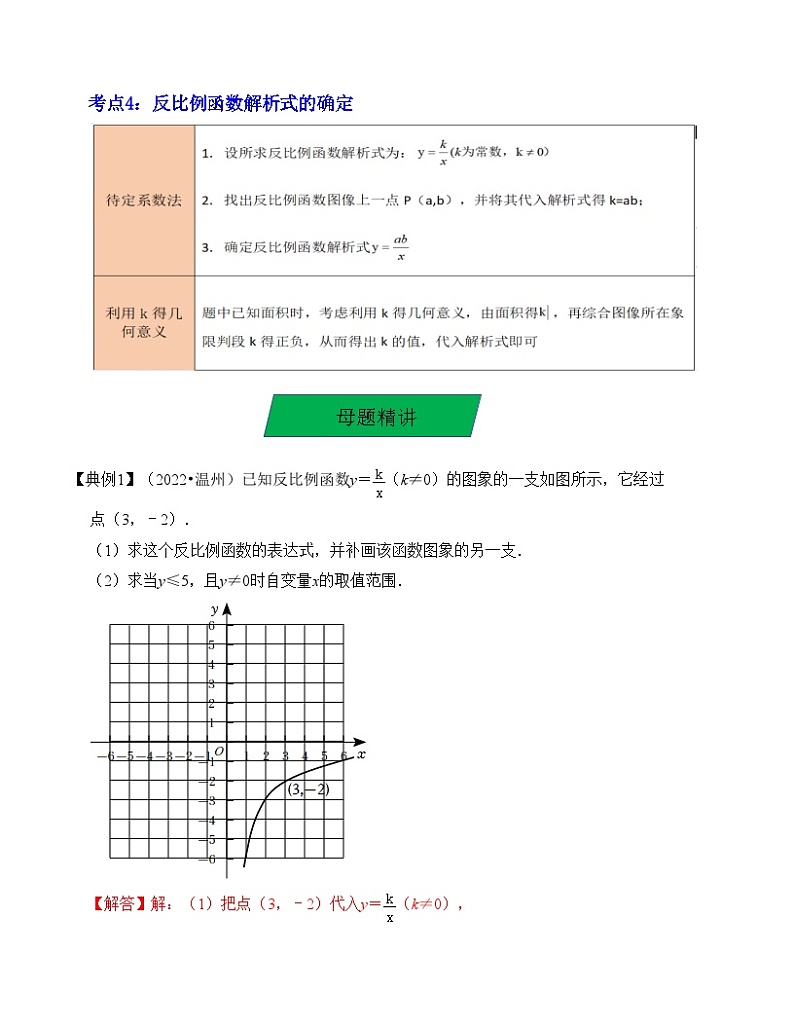
【典例1】（2022•温州）已知反比例函数y＝（k≠0）的图象的一支如图所示，它经过点（3，﹣2）．
（1）求这个反比例函数的表达式，并补画该函数图象的另一支．
（2）求当y≤5，且y≠0时自变量x的取值范围．
【解答】解：（1）把点（3，﹣2）代入y＝（k≠0），
﹣2＝，
解得：k＝﹣6，
∴反比例函数的表达式为y＝﹣，
补充其函数图象如下：
（2）当y＝5时，﹣＝5，
解得：x＝﹣，
∴当y≤5，且y≠0时，x≤﹣或x＞0
【典例2】（2022•安顺模拟）如图，一次函数y＝﹣x+3的图象与反比例函数y＝（x＞0）的图象交于A（1，a），B两
点，与x轴交于点C．
（1）求反比例函数的解析式和点B的坐标；
（2）根据图象，直接写出关于x的不等式﹣x+3＜的解集；
（3）若点P在x轴上，且S△APC＝5，求点P的坐标．
【解答】解：（1）把点A（1，a）代入y＝﹣x+3，得a＝2，
∴A（1，2）
把A（1，2）代入反比例函数y＝（k≠0），
∴k＝1×2＝2；
∴反比例函数的表达式为y＝；
联立解析式得：得或，
∴B（2，1），
（2）由图象可知，当x＞0时，不等式﹣x+3＜的解集0＜x＜1或x＞2；
（3）在直线y＝﹣x+3中，令y＝0，则x＝3，
∴C（3，0），
设P（m，0），
∴PC＝|m﹣3|，
∵△APC的面积为5，
∴|m﹣3|×2＝5，
∴|m﹣3|＝5，
∴m＝8或m＝﹣2，
∴P（8，0）或（﹣2，0）．
真题精选
命题1 反比例函数的图像及性质
1．（2022•阜新）已知反比例函数y＝（k≠0）的图象经过点（﹣2，4），那么该反比例函数图象也一定经过点（ ）
A．（4，2）B．（1，8）C．（﹣1，8）D．（﹣1，﹣8）
【答案】C
【解答】解：∵反比例函数y＝（k≠0）的图象经过点（﹣2，4），
∴k＝﹣2×4＝﹣8，
A、∵4×2＝8≠﹣8，∴此点不在反比例函数的图象上，故本选项错误；
B、∵1×8＝8≠﹣8，∴此点不在反比例函数的图象上，故本选项错误；
C、﹣1×8＝﹣8，∴此点在反比例函数的图象上，故本选项正确；
D、（﹣1）×（﹣8）＝8≠﹣8，∴此点不在反比例函数的图象上，故本选项错误．
故选：C．
2．（2022•襄阳）若点A（﹣2，y1），B（﹣1，y2）都在反比例函数y＝的图象上，则y1，y2的大小关系是（ ）
A．y1＜y2B．y1＝y2C．y1＞y2D．不能确定
【答案】C
【解答】解：∵点A（﹣2，y1），B（﹣1，y2）都在反比例函数y＝的图象上，k＝2＞0，
∴在每个象限内y随x的增大而减小，
∵﹣2＜﹣1，
∴y1＞y2，
故选：C．
3．（2021•郴州）在反比例函数y＝的图象的每一支曲线上，函数值y随自变量x的增大而增大，则m的取值范围是 ．
【答案】m＜3
【解答】解：反比例函数y＝图象上的每一条曲线上，y随x的增大而增大，
∴m﹣3＜0，
∴m＜3．
故答案为：m＜3．
命题2 反比例函数与一次函数结合
4．（2022•贺州）已知一次函数y＝kx+b的图象如图所示，则y＝﹣kx+b与y＝的图象为（ ）
A．B．
C．D．
【答案】A
【解答】解：根据一次函数y＝kx+b的图象位置，可判断k＞0、b＞0．
所以﹣k＜0．
再根据一次函数和反比例函数的图像和性质，
故选：A．
5．（2022•荆州）如图是同一直角坐标系中函数y1＝2x和y2＝的图象．观察图象可得不等式2x＞的解集为（ ）
A．﹣1＜x＜1B．x＜﹣1或x＞1
C．x＜﹣1或0＜x＜1D．﹣1＜x＜0或x＞1
【答案】D
【解答】解：由图象，函数y1＝2x和y2＝的交点横坐标为﹣1，1，
∴当﹣1＜x＜0或x＞1时，y1＞y2，即2x＞，
故选：D．
6．（2022•安顺模拟）如图，在平面直角坐标系中，一次函数y1＝kx+b的图象与反比例函数y2＝的图象交于A（4，1），B（﹣2，n）两点，与y轴交于点C．
（1）求一次函数与反比例函数的解析式；
（2）若点D在y轴上，且S△ABD＝12，求点D的坐标；
（3）当y1＞y2时，自变量x的取值范围为 ．
【解答】解：（1）∵反比例函数y2＝（m≠0）过点A（4，1），点B，
∴m＝4×1＝4，
∴反比例函数的解析式为y＝，
∵点B的横坐标为﹣2，
∴B（﹣2，﹣2），
把A（4，1），B（﹣2，﹣2）代入y1＝kx+b（k≠0）得，
解得，
∴一次函数的解析式为y＝x﹣1；
（2）由y＝x﹣1可知C（0，﹣1），
∵点D是y轴上一点，且S△ABD＝12，
∴S△ABD＝S△ACD+S△BCD＝CD•4+CD•2＝12，
∴CD＝4，
∴D（0，3）或（0，﹣5）；
（3）由图象可知，当y1＞y2时，自变量x的取值范围是﹣2＜x＜0或x＞4．
故答案为：﹣2＜x＜0或x＞4．
7．（2022•白山模拟）已知一次函数y＝kx+b（k≠0）与反比例函数（m≠0）的图象交于A（2，3），B（﹣6，n）两点．
（1）求一次函数和反比例函数的解析式；
（2）求△AOB的面积．
【解答】解：（1）∵反比例函数（m≠0）的图象过点A（2，3），
∴m＝2×3＝6，
∴反比例函数关系式为y＝，
当x＝﹣6时，y＝＝﹣1，
∴点B（﹣6，﹣1）．
又∵一次函数y＝kx+b（k≠0）的图象过点A（2，3），B（﹣6，﹣1）．
∴，
解得，
∴一次函数的关系式为：y＝x+2，
∴反比例函数关系式为，一次函数关系式为；
（2）如图，直线AB与y轴的交点C（0，2），即OC＝2，
∴S△AOB＝S△BOC+S△AOC
＝×2×6+×2×2
＝6+2
＝8，
即：△AOB的面积为8．命题3 反比例函数与几何图形结合
8．（2022•邵阳）如图是反比例函数y＝的图象，点A（x，y）是反比例函数图象上任意一点，过点A作AB⊥x轴于点B，连接OA，则△AOB的面积是（ ）
A．1B．C．2D．
【答案】B
【解答】解：∵A（x，y），
∴OB＝x，AB＝y，
∵A为反比例函数y＝图象上一点，
∴xy＝1，
∴S△ABO＝AB•OB＝xy＝1＝，
故选：B
9．（2022•黑龙江）如图，在平面直角坐标系中，点O为坐标原点，平行四边形OBAD的顶点B在反比例函数y＝的图象上，顶点A在反比例函数y＝的图象上，顶点D在x轴的负半轴上．若平行四边形OBAD的面积是5，则k的值是（ ）
A．2B．1C．﹣1D．﹣2
【答案】D
【解答】解：设B（a，），
∵四边形OBAD是平行四边形，
∴AB∥DO，
∴A（，），
∴AB＝a﹣，
∵平行四边形OBAD的面积是5，
∴（a﹣）＝5，
解得k＝﹣2，
故选：D．