中考数学一轮复习知识梳理+考点精讲专题16 一般三角形及其性质（2份，原卷版+解析版）

这是一份中考数学一轮复习知识梳理+考点精讲专题16 一般三角形及其性质（2份，原卷版+解析版），文件包含中考数学一轮复习知识梳理+考点精讲专题16一般三角形及其性质原卷版doc、中考数学一轮复习知识梳理+考点精讲专题16一般三角形及其性质解析版doc等2份试卷配套教学资源，其中试卷共17页， 欢迎下载使用。

三角形的性质是初中数学的基本内容之一．预计在中考的分值为6分左右．题型多是填空题、选择题．中考对这部分内容的考查主要包括三角形的边角关系。
考标要求
1.理解三角形有关的中线、角平分线、高线，并会作三角形的中线、角平分线、高线；
2.理解并掌握三角形的中位线的性质；
3.理解三角形的三边关系，并能确定三角形第三边的取值范围；
4.掌握三角形的内角和定理，并会证明三角形的内角和定理；
5.能利用三角形的外角进行角的有关计算与证明。
考点精讲
考点1：三角形的分类

考点2：三角形边角关系
（1）三边关系：三角形任意两边的和大于第三边，任意两边的差小于第三边。
（2）三角形内角和定理：三角形三个内角的和等于 180 度。
（3）三角形的一个外角等于与它不相邻的两个内角和；三角形的一个外角大于与它不相 邻的任何一个角。
考点3：三角形的重要线段
母题精讲
【典例1】（2022•凉山州）下列长度的三条线段能组成三角形的是（ ）
A．3，4，8B．5，6，11C．5，6，10D．5，5，10
【答案】C
【解答】解：A.3+4＜8，不能组成三角形，不符合题意；
B.5+6＝11，不能组成三角形，不符合题意；
C.5+6＞10，能组成三角形，符合题意；
D.5+5＝10，不能组成三角形，不符合题意．
故选：C．
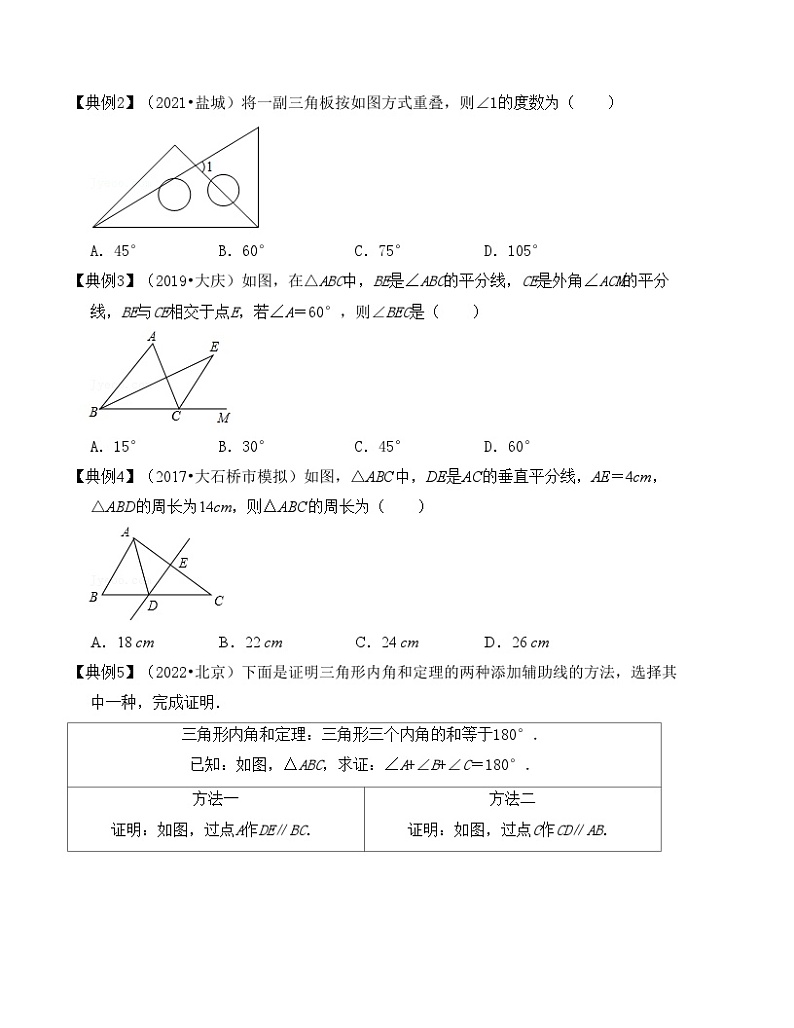
【典例2】（2021•盐城）将一副三角板按如图方式重叠，则∠1的度数为（ ）
A．45°B．60°C．75°D．105°
【答案】C
【解答】解：根据三角板的度数知，∠ABC＝∠ACB＝45°，∠DBC＝30°，
∴∠1＝∠DBC+∠ACB＝30°+45°＝75°，
故选：C．
【典例3】（2019•大庆）如图，在△ABC中，BE是∠ABC的平分线，CE是外角∠ACM的平分线，BE与CE相交于点E，若∠A＝60°，则∠BEC是（ ）
A．15°B．30°C．45°D．60°
【答案】B
【解答】解：∵BE是∠ABC的平分线，
∴∠EBM＝∠ABC，
∵CE是外角∠ACM的平分线，
∴∠ECM＝∠ACM，
则∠BEC＝∠ECM﹣∠EBM＝×（∠ACM﹣∠ABC）＝∠A＝30°，
故选：B．
【典例4】（2017•大石桥市模拟）如图，△ABC中，DE是AC的垂直平分线，AE＝4cm，△ABD的周长为14cm，则△ABC的周长为（ ）
A．18 cmB．22 cmC．24 cmD．26 cm
【答案】B
【解答】解：∵DE是AC的垂直平分线，
∴DA＝DC，AE＝EC＝4cm，
而△ABD的周长为14cm，即AB+BD+AD＝14cm，
∴AB+BD+DC＝14cm，
∴AB+BC+AC＝14cm+8cm＝22cm，
即△ABC的周长为22cm．
故选：B．
【典例5】（2022•北京）下面是证明三角形内角和定理的两种添加辅助线的方法，选择其中一种，完成证明．
【解答】证明：方法一：∵DE∥BC，
∴∠B＝∠BAD，∠C＝∠CAE，
∵∠BAD+∠BAC+∠CAE＝180°，
∴∠B+∠BAC+∠C＝180°；
方法二：∵CD∥AB，
∴∠A＝∠ACD，∠B+∠BCD＝180°，
∴∠B+∠ACB+∠A＝180°．
真题精选
命题1 三角形的基本性质
1．（2018•柳州）如图，图中直角三角形共有（ ）
A．1个B．2个C．3个D．4个
【答案】C
【解答】解：如图，图中直角三角形有Rt△ABD、Rt△BDC、Rt△ABC，共有3个，
故选：C．
2．（2021•绥化）下列命题是假命题的是（ ）
A．任意一个三角形中，三角形两边的差小于第三边
B．三角形的中位线平行于三角形的第三边，并且等于第三边的一半
C．如果一个角的两边分别平行于另一个角的两边，那么这两个角一定相等
D．一组对边平行且相等的四边形是平行四边形
【答案】C
【解答】解：A、任意一个三角形中，三角形两边的差小于第三边，正确，是真命题，不符合题意；
B、三角形的中位线平行于三角形的第三边，并且等于第三边的一半，正确，是真命题，不符合题意；
C、如果一个角的两边分别平行于另一个角的两边，那么这两个角一定相等或互补，故原命题错误，是假命题，符合题意；
D、一组对边平行且相等的四边形是平行四边形，正确，是真命题，不符合题意，
故选：C
3．（2020•锦州）如图，在△ABC中，∠A＝30°，∠B＝50°，CD平分∠ACB，则∠ADC的度数是（ ）
A．80°B．90°C．100°D．110°
【答案】C
【解答】解：∵∠A＝30°，∠B＝50°，
∴∠ACB＝180°﹣30°﹣50°＝100°（三角形内角和定义）．
∵CD平分∠ACB，
∴∠BCD＝∠ACB＝×100°＝50°，
∴∠ADC＝∠BCD+∠B＝50°+50°＝100°．
故选：C．
4．（2021•河池）如图，∠A＝40°，∠CBD是△ABC的外角，∠CBD＝120°，则∠C的大小是（ ）
A．90°B．80°C．60°D．40°
【解答】解：由三角形的外角性质得，∠C＝∠CBD﹣∠A＝120°﹣40°＝80°．
故选：B．
命题2 三角形中的特殊线段及其性质
5．（2022•玉林）请你量一量如图△ABC中BC边上的高的长度，下列最接近的是（ ）
A．0.5cmB．0.7cmC．1.5cmD．2cm
【答案】D
【解答】解：过点A作AD⊥BC于D，
用刻度尺测量AD的长度，更接近2cm，
故选：D．
6．（2022•常州）如图，在△ABC中，E是中线AD的中点．若△AEC的面积是1，则△ABD的面积是 ．
【答案】2
【解答】解：∵E是AD的中点，
∴CE是△ACD的中线，
∴S△ACD＝2S△AEC，
∵△AEC的面积是1，
∴S△ACD＝2S△AEC＝2，
∵AD是△ABC的中线，
∴S△ABD＝S△ACD＝2．
故答案为：2
7．（2021•长沙）如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，DE⊥AB，垂足为E，若BC＝4，DE＝1.6，则BD的长为 ．
【答案】2.4
【解答】解：∵AD平分∠BAC，DE⊥AB，∠C＝90°，
∴CD＝DE，
∵DE＝1.6，
∴CD＝1.6，
∴BD＝BC﹣CD＝4﹣1.6＝2.4．
故答案为：2.4
三角形内角和定理：三角形三个内角的和等于180°．
已知：如图，△ABC，求证：∠A+∠B+∠C＝180°．
方法一
证明：如图，过点A作DE∥BC．
方法二
证明：如图，过点C作CD∥AB．