中考数学一轮复习知识梳理+考点精讲专题23 菱形的性质与判定（2份，原卷版+解析版）

这是一份中考数学一轮复习知识梳理+考点精讲专题23 菱形的性质与判定（2份，原卷版+解析版），文件包含中考数学一轮复习知识梳理+考点精讲专题23菱形的性质与判定原卷版doc、中考数学一轮复习知识梳理+考点精讲专题23菱形的性质与判定解析版doc等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。

菱形是一种特殊的平行四边形,也是中考的必考内容.为考查同学们分析能力、想象能力、探究能力和创新能力,菱形开放题便成了各地中考命题的热点。
考标要求
1.掌握菱形的概念、判定和性质，会用菱形的性质和判；
2.会运用菱形的知识解决有关菱形定解决简单问题问题。
考点精讲
考点1：菱形的定义
有一组邻边相等的平行四边形叫做菱形。
考点2：菱形的性质
（1） 菱形的四条边都相等；
（2）菱形的两条对角线互相垂直，并且每一条对角线平分一组对角。
考点3：菱形的判定定理
（1）一组邻边相等的平行四边形是菱形；
（2）对角线互相垂直的平行四边形是菱形；
（3）四条边相等的四边形是菱形。
考点4：菱形的面积
S=ah=mn/2（菱形底边长为a，高为h，两条对角线长分别为m和n）
母题精讲
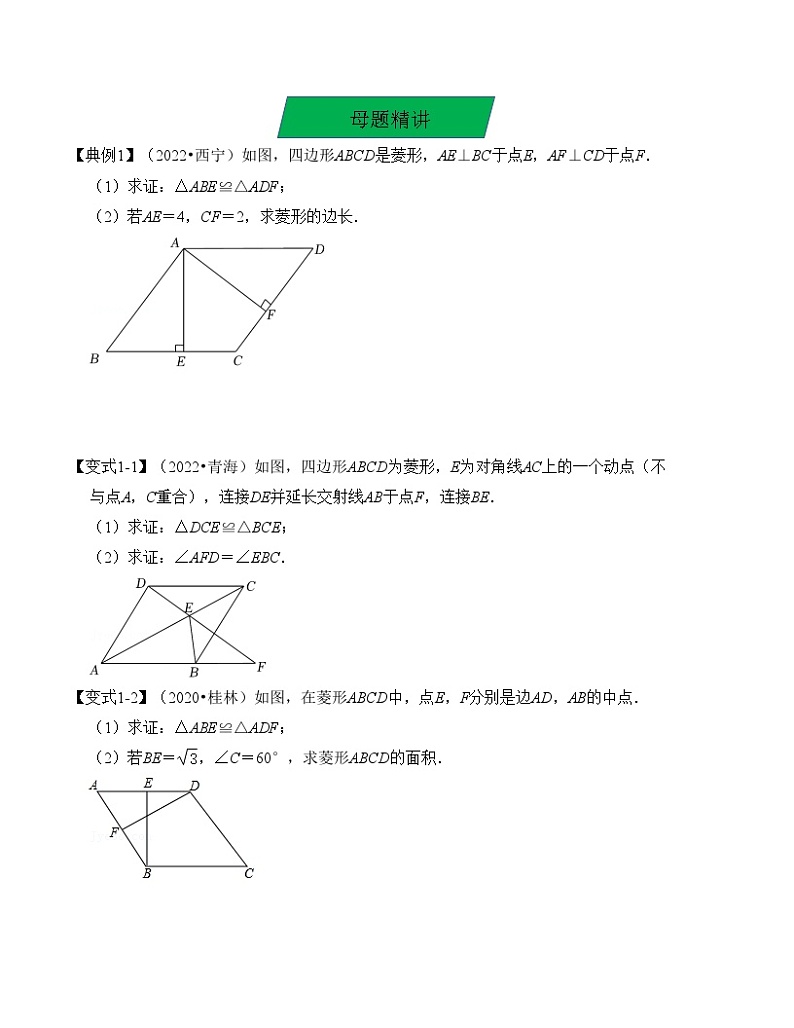
【典例1】（2022•西宁）如图，四边形ABCD是菱形，AE⊥BC于点E，AF⊥CD于点F．
（1）求证：△ABE≌△ADF；
（2）若AE＝4，CF＝2，求菱形的边长．
【解答】（1）证明：∵四边形ABCD是菱形，
∴AB＝BC＝CD＝AD，∠B＝∠D，
∵AE⊥BC，AF⊥CD，
∴∠AEB＝∠AFD，
在△ABE和△ADF中，
，
∴△ABE≌△ADF（AAS）；
（2）解：设菱形的边长为x，
∵AB＝CD＝x，CF＝2，
∴DF＝x﹣2，
∵△ABE≌△ADF，
∴BE＝DF＝x﹣2，
在Rt△ABE中，根据勾股定理得，
AE2+BE2＝AB2，
即42+（x﹣2）2＝x2，
解得x＝5，
∴菱形的边长是5．
【变式1-1】（2022•青海）如图，四边形ABCD为菱形，E为对角线AC上的一个动点（不与点A，C重合），连接DE并延长交射线AB于点F，连接BE．
（1）求证：△DCE≌△BCE；
（2）求证：∠AFD＝∠EBC．
【解答】证明：（1）∵四边形ABCD是菱形，
∴CD＝CB，∠DCE＝∠BCE，
∵CE＝CE，
∴△DCE≌△BCE（SAS）；
（2）∵四边形ABCD是菱形，
∴DC∥AF，
∴∠CDF＝∠AFD，
∵△DCE≌△BCE，
∴∠CDF＝∠EBC，
∴∠AFD＝∠EBC．
【变式1-2】（2020•桂林）如图，在菱形ABCD中，点E，F分别是边AD，AB的中点．
（1）求证：△ABE≌△ADF；
（2）若BE＝，∠C＝60°，求菱形ABCD的面积．
【解答】（1）证明：∵四边形ABCD是菱形，
∴AB＝AD，
∵点E，F分别是边AD，AB的中点，
∴AF＝AE，
在△ABE和△ADF中，，
∴△ABE≌△ADF（SAS）；
（2）解：连接BD，如图：
∵四边形ABCD是菱形，
∴AB＝AD，∠A＝∠C＝60°，
∴△ABD是等边三角形，
∵点E是边AD的中点，
∴BE⊥AD，
∴∠ABE＝30°，
∴AE＝tan30°BE＝BE＝1，AB＝2AE＝2，
∴AD＝AB＝2，
∴菱形ABCD的面积＝AD×BE＝2×＝2．
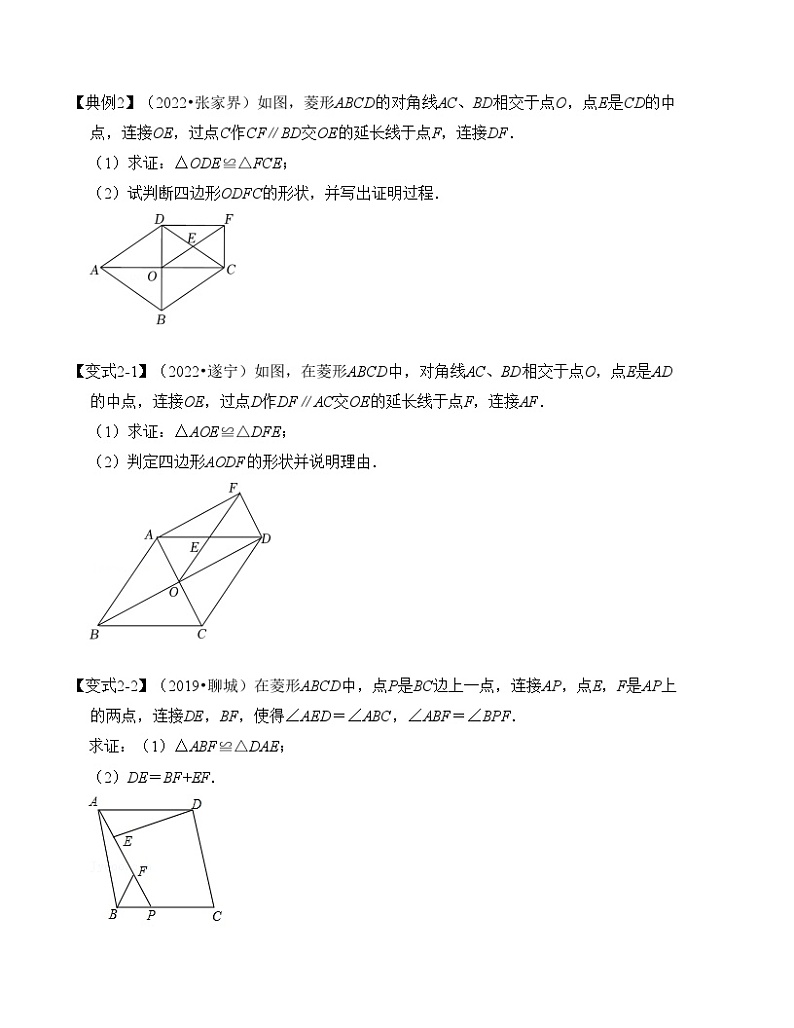
【典例2】（2022•张家界）如图，菱形ABCD的对角线AC、BD相交于点O，点E是CD的中点，连接OE，过点C作CF∥BD交OE的延长线于点F，连接DF．
（1）求证：△ODE≌△FCE；
（2）试判断四边形ODFC的形状，并写出证明过程．
【解答】（1）证明：∵点E是CD的中点，
∴CE＝DE，
又∵CF∥BD
∴∠ODE＝∠FCE，
在△ODE和△FCE中，
，
∴△ODE≌△FCE（ASA）；
（2）解：四边形ODFC为矩形，证明如下：
∵△ODE≌△FCE，
∴OE＝FE，
又∵CE＝DE，
∴四边形ODFC为平行四边形，
又∵四边形ABCD为菱形，
∴AC⊥BD，
即∠DOC＝90°，
∴四边形ODFC为矩形．
【变式2-1】（2022•遂宁）如图，在菱形ABCD中，对角线AC、BD相交于点O，点E是AD的中点，连接OE，过点D作DF∥AC交OE的延长线于点F，连接AF．
（1）求证：△AOE≌△DFE；
（2）判定四边形AODF的形状并说明理由．
【解答】（1）证明：∵E是AD的中点，
∴AE＝DE，
∵DF∥AC，
∴∠OAD＝∠ADF，
∵∠AEO＝∠DEF，
∴△AOE≌△DFE（ASA）．
（2）解：四边形AODF为矩形．
理由：∵△AOE≌△DFE，
∴AO＝DF，
∵DF∥AC，
∴四边形AODF为平行四边形，
∵四边形ABCD为菱形，
∴AC⊥BD，
即∠AOD＝90°，
∴平行四边形AODF为矩形．
【变式2-2】（2019•聊城）在菱形ABCD中，点P是BC边上一点，连接AP，点E，F是AP上的两点，连接DE，BF，使得∠AED＝∠ABC，∠ABF＝∠BPF．
求证：（1）△ABF≌△DAE；
（2）DE＝BF+EF．
【解答】证明：（1）∵四边形ABCD是菱形，
∴AB＝AD，AD∥BC，
∴∠BPA＝∠DAE，
∵∠ABC＝∠AED，
∴∠BAF＝∠ADE，
∵∠ABF＝∠BPF，∠BPA＝∠DAE，
∴∠ABF＝∠DAE，
∵AB＝DA，
∴△ABF≌△DAE（ASA）；
（2）∵△ABF≌△DAE，
∴AE＝BF，DE＝AF，
∵AF＝AE+EF＝BF+EF，
∴DE＝BF+EF．
【典例3】（2022•北京）如图，在▱ABCD中，AC，BD交于点O，点E，F在AC上，AE＝CF．
（1）求证：四边形EBFD是平行四边形；
（2）若∠BAC＝∠DAC，求证：四边形EBFD是菱形．
【解答】证明：（1）在▱ABCD中，OA＝OC，OB＝OD，
∵AE＝CF．
∴OE＝OF，
∴四边形EBFD是平行四边形；
（2）∵四边形ABCD是平行四边形，
∴AB∥DC，
∴∠BAC＝∠DCA，
∵∠BAC＝∠DAC，
∴∠DCA＝∠DAC，
∴DA＝DC，
∴平行四边形ABCD为菱形，
∴DB⊥EF，
∴平行四边形EBFD是菱形．
【变式3-1】（2019•兰州）如图，AC＝8，分别以A、C为圆心，以长度5为半径作弧，两条弧分别相交于点B和D．依次连接A、B、C、D，连接BD交AC于点O．
（1）判断四边形ABCD的形状并说明理由；
（2）求BD的长．
【解答】解：（1）四边形ABCD为菱形；
由作法得AB＝AD＝CB＝CD＝5，
所以四边形ABCD为菱形；
（2）∵四边形ABCD为菱形，
∴OA＝OC＝4，OB＝OD，AC⊥BD，
在Rt△AOB中，OB＝＝3，
∴BD＝2OB＝6．
【变式3-2】（2022•舟山）小惠自编一题：“如图，在四边形ABCD中，对角线AC，BD交于点O，AC⊥BD，OB＝OD．求证：四边形ABCD是菱形”，并将自己的证明过程与同学小洁交流．
若赞同小惠的证法，请在第一个方框内打“√”；若赞成小洁的说法，请你补充一个条件，并证明．
【解答】解：赞成小洁的说法，补充条件：OA＝OC，证明如下：
∵OA＝OC，OB＝OD，
∴四边形ABCD是平行四边形，
又∵AC⊥BD，
∴平行四边形ABCD是菱形．
真题精选
命题点1 菱形的判定
1．（2022•襄阳）如图，▱ABCD的对角线AC和BD相交于点O，下列说法正确的是（ ）
A．若OB＝OD，则▱ABCD是菱形
B．若AC＝BD，则▱ABCD是菱形
C．若OA＝OD，则▱ABCD是菱形
D．若AC⊥BD，则▱ABCD是菱形
【答案】D
【解答】解：A、∵四边形ABCD是平行四边形，
∴OB＝OD，故选项A不符合题意；
B、∵四边形ABCD是平行四边形，AC＝BD，
∴▱ABCD是矩形，故选项B不符合题意；
C、∵四边形ABCD是平行四边形，
∴OA＝OC＝AC，OB＝OD＝BD，
∵OA＝OD，
∴AC＝BD，
∴▱ABCD是矩形，故选项C不符合题意；
D、∵四边形ABCD是平行四边形，AC⊥BD，
∴▱ABCD是菱形，故选项D符合题意；
故选：D
2．（2019•青海）如图，在△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F，连接CF．
（1）求证：△AEF≌△DEB；
（2）证明：四边形ADCF是菱形．
【解答】证明：（1）∵AF∥BC，
∴∠AFE＝∠DBE
∵△ABC是直角三角形，AD是BC边上的中线，E是AD的中点，
∴AE＝DE，BD＝CD
在△AFE和△DBE中，
，
∴△AFE≌△DBE（AAS）
（2）由（1）知，AF＝BD，且BD＝CD，
∴AF＝CD，且AF∥BC，
∴四边形ADCF是平行四边形
∵∠BAC＝90°，D是BC的中点，
∴AD＝BC＝CD，
∴四边形ADCF是菱形．
命题点2 菱形的性质及其应用
3．（2022•兰州）如图，菱形ABCD的对角线AC与BD相交于点O，E为AD的中点，连接OE，∠ABC＝60°，BD＝4，则OE＝（ ）
A．4B．2C．2D．
【答案】C
【解答】解：∵四边形ABCD是菱形，∠ABC＝60°，
∴BO＝DO，∠ABO＝30°，AC⊥BD，AB＝AD，
∴BO＝2，
∴AO＝＝2，
∴AB＝2AO＝4，
∵E为AD的中点，∠AOD＝90°，
∴OE＝AD＝2，
故选：C
4．（2022•河池）如图，在菱形ABCD中，对角线AC，BD相交于点O，下列结论中错误的是（ ）
A．AB＝ADB．AC⊥BDC．AC＝BDD．∠DAC＝∠BAC
【答案】C
【解答】解：∵四边形ABCD是菱形，
∴∠BAC＝∠DAC，AB＝AD，AC⊥BD，
故A、B、D正确，无法得出AC＝BD，
故选：C．
5．（2022•自贡）如图，菱形ABCD对角线交点与坐标原点O重合，点A（﹣2，5），则点C的坐标是（ ）
A．（5，﹣2）B．（2，﹣5）C．（2，5）D．（﹣2，﹣5）
【答案】B
【解答】解：∵四边形ABCD是菱形，
∴OA＝OC，即点A与点C关于原点对称，
∵点A（﹣2，5），
∴点C的坐标是（2，﹣5）．
故选：B．
6．（2022•乐山）已知菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm．则菱形的面积为 cm2．
【答案】24
【解答】解：∵菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm，
∴菱形的面积是＝24（cm2），
故答案为：24．
7．（2022•大连）如图，四边形ABCD是菱形，点E，F分别在AB，AD上，AE＝AF．求证：CE＝CF．
【解答】证明：如图，连接AC，
∵四边形ABCD是菱形，
∴∠EAC＝∠FAC，
在△ACE和△ACF中，
，
∴△ACE≌△ACF（SAS）
∴CE＝CF．
8．（2022•广元）如图，在四边形ABCD中，AB∥CD，AC平分∠DAB，AB＝2CD，E为AB中点，连结CE．
（1）求证：四边形AECD为菱形；
（2）若∠D＝120°，DC＝2，求△ABC的面积．
【解答】（1）证明：∵E为AB中点，
∴AB＝2AE＝2BE，
∵AB＝2CD，
∴CD＝AE，
又∵AE∥CD，
∴四边形AECD是平行四边形，
∵AC平分∠DAB，
∴∠DAC＝∠EAC，
∵AB∥CD，
∴∠DCA＝∠CAB，
∴∠DCA＝∠DAC，
∴AD＝CD，
∴平行四边形AECD是菱形；
（2）∵四边形AECD是菱形，∠D＝120°，
∴AD＝CD＝CE＝AE＝2，∠D＝120°＝∠AEC，
∴AE＝CE＝BE，∠CEB＝60°，
∴∠CAE＝30°＝∠ACE，△CEB是等边三角形，
∴BE＝BC＝EC＝2，∠B＝60°，
∴∠ACB＝90°，
∴AC＝BC＝2，
∴S△ABC＝×AC×BC＝×2×2＝2．
小惠：
证明：∵AC⊥BD，OB＝OD，
∴AC垂直平分BD．
∴AB＝AD，CB＝CD，
∴四边形ABCD是菱形．
小洁：
这个题目还缺少条件，需要补充一个条件才能证明．