






北师大版(2024)七年级下册(2024)1 幂的乘除说课ppt课件
展开
这是一份北师大版(2024)七年级下册(2024)1 幂的乘除说课ppt课件,共31页。PPT课件主要包含了mn都是正整数,幂的乘方法则,积的乘方法则,n是正整数,÷109,同底数幂的除法,是相同底数的幂相除,个10,由此你发现了什么,210m÷10n等内容,欢迎下载使用。
我们在前面学习了与幂有关的运算性质,这些运算都有哪些?
1.同底数幂乘法法则:
一种液体每升含有 1012 个有害细菌。为了试验某种灭菌剂的效果,科学家进行了实验,发现 1 滴灭菌剂可以杀死 109 个有害细菌。要将 1 L 液体中的有害细菌全部杀死, 需要这种灭菌剂多少滴? 你是怎样计算的?
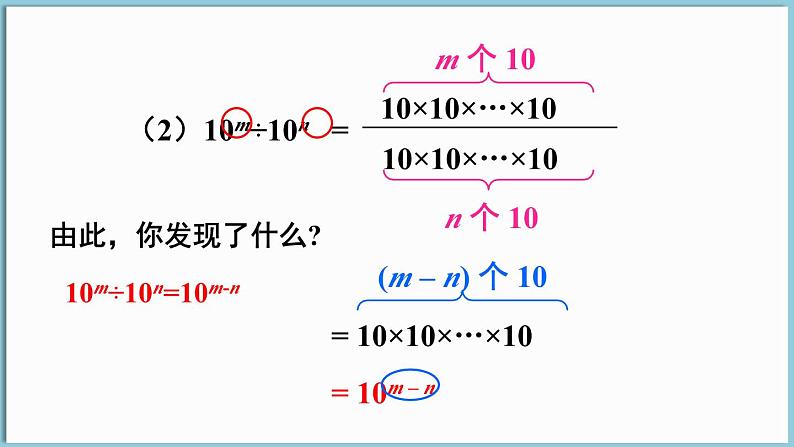
同底数的幂相除,怎样计算呢?
观察这个算式,它有何特点?
1.计算下列各式,并说明理由(m>n)。
(1)1012÷109;(2)10m÷10n;(3)(-3)m ÷ (-3)n 。
(1)1012÷109
= 10×10×…×10
(12 – 9) 个10
1012÷109=1012-9
(m – n) 个 10
10m÷10n=10m-n
(3)(– 3)m÷ (– 3) n
= (– 3) m – n
= (– 3) × (– 3) ×…× (– 3)
(m – n) 个 (– 3)
(-3)m÷(-3) n=(-3)m-n
2.如果m,n都是正整数,且m>n,那么am÷an等于什么?你是怎样得到的?
= a · a · … · a
(m – n) 个 a
即am÷an= am – n(m>n,且m,n都是正整数)
同底数幂的除法和同底数幂的乘法互为逆运算,因此同底数幂的除法可以用同底数幂的乘法来检验。
a可以是单项式或多项式,但不能为0。
(1) a7÷a4; (2) (– x)6÷(– x)3;
(3) (xy)4÷(xy); (4) b2m+2÷b2 。
解:(1) a7÷a4 = a7 – 4 = a3;
(2) (– x)6÷(– x)3 = (– x)6 – 3 = (– x)3 = – x3;
(3) (xy)4÷(xy) = (xy)4–1 = (xy)3 = x3y3 ;
(4) b2m+2÷b2 = b2m+2–2 = b2m 。
我们已经得到了当m>n时,am÷an(a≠0) 的运算法则,其中m、n都是正整数。 那么当m≤n时,am÷an(a≠0) 又如何计算?
计算:(1)23÷23;(2)a3÷a3。
(1)23÷23=23-3=20,
(2)a3÷a3=a3-3=a0,
根据同底数幂除法法则计算:
任何一个不等于0的数的0次幂都等于1。
注意: 零指数幂的底数可以是单项式,也可以是多项式,但是不能为0。
计算:(1)23÷25;(2)a3÷a5。
23÷25=23-5=2-2,
a3÷a5=a3-5=a-2。
任何不等于零的数的-p(p是正整数)次幂等于这个数的p次幂的倒数。
am ÷ an = am – n(a ≠ 0,m,n 都是正整数)
例 6 用小数或分数表示下列各数:
(1)10 –3;(2)70×8 –2;(3)1.6×10 –4 。
(1)x12÷x4;(2)(-y)3÷(-y)2;(3)-(k6÷k6) ; (4)(-r)5÷r4;(5)m÷m0;(6)(mn)5÷(mn) 。
解:(1)x12÷x4 =x12-4 = x8;
(2) (-y)3÷(-y)2 =-y;
(3) -(k6÷k6) =-1;
(4) (-r)5÷r4 =-r5÷r4=-r ;
(5) m÷m0=m÷1= m;
(6) (mn)5÷(mn) = (mn)5-1 =(mn)4=m4n4。
有的细胞的直径只有 1 微米(μm), 即 0.000 001 m; 某种计算机完成一次基本运算的时间约为 1纳秒(ns), 即 0.000 000 001 s; 一个氧原子的质量为 0.000 000 000 000 000 000 000 000 026 57 kg 。
你能用负指数表示这些数吗?
用科学记数法可以很方便地表示一些绝对值较大的数,同样,用科学记数法也可以很方便地表示一些绝对值较小的数。
= 10 – 3 ……
大于-1的负数也可以用类似的方法表示,如-0.000 002 56=-2.56×10-6。
1. 用科学记数法表示下列各数:(1)0.000 003 2 = (2)– 0.000 000 14 =(3)– 680 000 000 =(4)314 000 000 000 =
– 1.4×10 – 7
2. 1个电子的质量约为0.000 000 000 000 000 000 000 000 000 000 911 kg,请用科学记数法表示这个数。
解: 0.000 000 000 000 000 000 000 000 000 000 911 =9.11×10-31。
1. (1)计算: x10÷x4÷x2 = ______。 (2)(– ax)5÷(ax)3 = ______。
2. 计算:(1)(xy)5÷(xy)3÷(– xy);(2)(x – y)10÷(y – x)4·(x – y)2。
原式 = (x – y)8
3. 用科学记数法表示下列各数:(1)0.002 1;(2)0.000 1;(3)0.000 305;(4)– 0.000 000 08。
3.05×10 – 4
4. 写出下列各数的原数:(1)1.35×10 – 6 ;(2)5.0×10 – 3。
5. 1 纳米 = 10 – 9 米,将 0.003 05 纳米用科学记数法表示为_____________米。
0.000 001 35
3.05×10 – 12
6. 若 2x = 3,2y = 6,2z = 12,求 x,y,z 之间的数量关系。
解:因为 2y÷2x = 2y – x = 6÷3 = 2, 2z÷2y = 2z – y = 2,所以 2y – x = 2z – y, 即 y – x = z – y,所以 2y = x + z 。
7. 一根头发丝的直径为 6 万 nm(纳米),某种生物细胞的直径为 1 μm(微米)。请你选择适当的方法说明两者之间的差距(1 nm = 10 – 9m,1 μm = 10 – 6m)。
解:因为 6 万 nm = 6×104×10 – 9 m = 6×10 – 5 m,所以 6×10 – 5÷(1×10 – 6) = 6×10 – 5+6 = 60,即一根头发丝的直径是该种生物细胞直径的 60 倍。
相关课件
这是一份初中数学北师大版(2024)七年级下册(2024)1 幂的乘除教学ppt课件,共18页。PPT课件主要包含了x15,am+n,amn,等于多少呢,这个式子有什么特点,34×54,3m×5m,anbn,n个ab,n个a等内容,欢迎下载使用。
这是一份数学七年级下册(2024)1 幂的乘除图片课件ppt,共24页。PPT课件主要包含了思考什么叫乘方,计算下列各式,1102×103,2105×108,10×10,310m×10n,10m+n,2m×2n,2m+n,–3m+n等内容,欢迎下载使用。
这是一份数学七年级下册(2024)1 幂的乘除课文内容课件ppt,共26页。PPT课件主要包含了÷109,am-n,同底数幂的除法法则等内容,欢迎下载使用。









