初中数学北师大版（2024）七年级下册（2024）2 整式的乘法集体备课ppt课件

这是一份初中数学北师大版（2024）七年级下册（2024）2 整式的乘法集体备课ppt课件，共25页。PPT课件主要包含了a·2b+3a，ab+3a2，你发现了什么，乘法的分配律，例2计算，看作整体，多项式×多项式，例3计算，由题意得，b–2等内容，欢迎下载使用。
1.什么是单项式乘单项式法则?
单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，其余字母连同它的指数不变，作为积的因式。
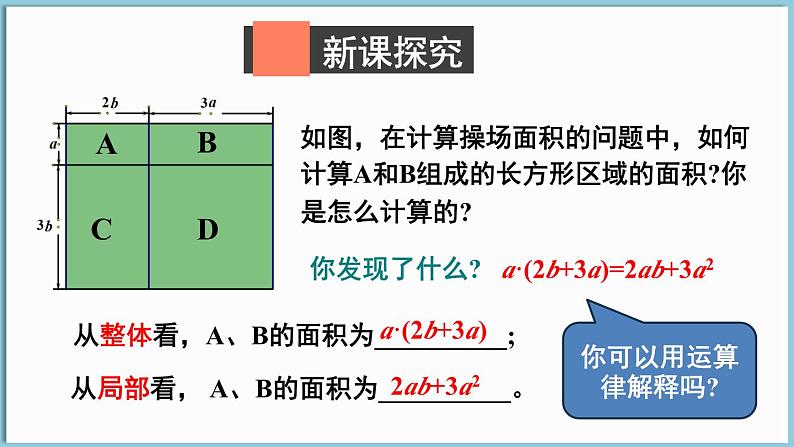
如图，在计算操场面积的问题中，如何计算A和B组成的长方形区域的面积?你是怎么计算的?
从整体看，A、B的面积为__________;
从局部看， A、B的面积为__________。
a·(2b+3a)=2ab+3a2
你可以用运算律解释吗?
(2) a (2b+3a)=2ab+3a2，你能用运算律解释吗?
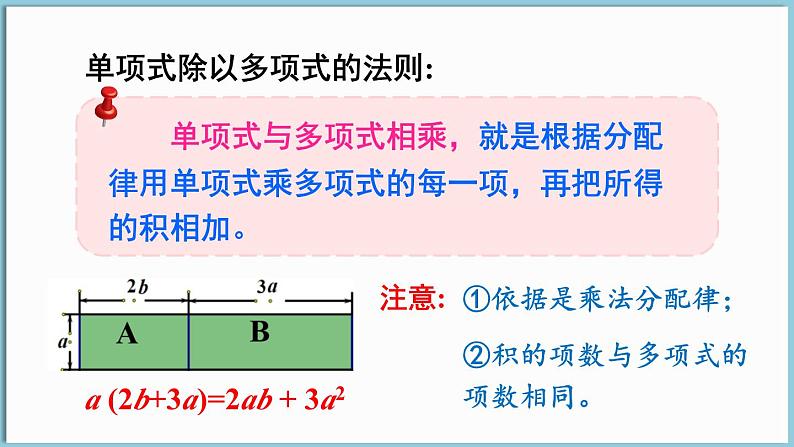
a (2b+3a)=2ab + 3a2
p(a+b+c)=pa+pb+pc
当p、a、b、c为单项式时，乘法分配律也成立。
你能计算ab·(abc+2x) ， c2·(m+n–p)，(x2y+xy2)·(–xy) 吗?
ab·(abc + 2x) = ab·abc+ab·2x
= a2b2c+2abx
c2·(m + n – p) = c2m+c2n – c2p
(x2y+xy2)·(– xy) = –x3y2–x2y3
一般地，如何进行单项式乘多项式的运算?与同伴进行交流。
单项式除以多项式的法则:
（1） 2ab ( 5ab2 + 3a2b )； （2） ( ab2 – 2ab )· ab ； （3） 5m2n ( 2n + 3m – n2 )；（4） 2 ( x + y2z + xy2z3 )·xyz。
（1）a (a2m+n)；
（2）b2 (b+3a–a2 )；
（4）4 (e+f 2d ) ·ef 2d。
解：（1）a (a2m+n)=a3m+an；
（2）b2 (b+3a–a2 )=b3+3ab2–a2b2 ；
（4）4 (e+f 2d ) ·ef 2d=4e2f 2d+4ef 4d 2 。
如图，如何计算整个操场的面积?
方法1：将ABCD看成一个整体，可得
(a+3b)·(2b+3a)
方法2：将AB，CD分别看成一个整体，可得
a·(2b+3a)+3b·(2b+3a)
方法3：将AC，BD分别看成一个整体，可得
2b·(a+3b)+3a·(a+3b)
方法4:分别求出ABCD的面积并求和，可得
2ab+3a2+6b2+9ab
相等，都表示操场的面积。
=a·(2b+3a)+3b·(2b+3a)
=2ab+3a2+6b2+9ab
=2b·(a+3b)+3a·(a+3b)
一般地，如何进行多项式乘多项式的运算?与同伴进行交流。
你能计算(2a+b)·(a+2b) ，(x–y)·(x–1) ，(a2–b2)·(a–b) 吗?
(2a+b)·(a+2b)
(x–y)·(x–1)
=2a(a+2b) +b(a+2b)
=2a2+4ab+ab+2b2
=2a2+5ab+2b2 。
(a2–b2)·(a–b)
=x(x–1)–y(x–1)
=x2–x–xy+y 。
=a(a2–b2)–b(a2–b2)
=a3–ab2–ba2b+b3。
多项式与多项式相乘的运算法则:
（1） ( 1 – x ) ( 0.6 – x )； （2） ( 2x + y ) ( x – y )。
解：（1）( 1 – x ) ( 0.6 – x ) = 1 × 0.6 – 1 · x – x · 0.6 + x · x = 0.6 –x –0.6 x + x2 = 0.6 –1.6 x + x2；
（2）( 2x + y ) ( x – y ) = 2x·x – 2x·y + y·x – y·y = 2x2 – 2xy + xy – y2 = 2x2 – xy – y2。
解：（1） (x+y)(a+2b) = ax+2bx+ay+2by；
（3）(2x+3)(–x–1)。
（1）(x+y)(a+2b)；
（3） (2x+3)(–x–1) = –2x2–2x–3x–3= –2x2–5x–3。
1.计算：(1) 5x · (3x + 4)
解：(1) 原式= 15x2 + 20x；
(2) 原式 = – 15a3 + 4a2 – 3a；
（3）(x + 2)(x2 – 2x + 4)；
（4）(x – y)2 – (x – 2y)(x + y)。
(3)原式 = x3 + 8；
(4)原式 = 3y2 – xy。
2. 某长方体的长为 a + 1，宽为 a，高为 3， 问这个长方体的体积是多少?
解： (a + 1) · a×3= 3a(a + 1)= 3a2 + 3a
3. 要使 x(x2 + a + 3) = x(x2 + 5) + 2(b + 2) 成立，则常数 a，b 的值分别为多少?
解：∵ x(x2 + a + 3) = x(x2 + 5) + 2(b + 2) ∴ x3 + (a + 3)x = x3 + 5x + 2(b + 2)
(a + 3) = 5
2(b + 2) = 0
4.计算： (a + b + c)(c + d + e)。
解: (a + b + c)(c + d + e)
= ac+bc+c2+ad+bd+cd+ae+be+ce。
= (a+b+c)c+(a+b+c)d+(a+b+c)e
5. 当 x = 7 时，求代数式 (2x + 5)(x + 1) – (x – 3)(x + 1) 的值。
解：化简原式，得 x2 + 9x + 8， 当 x = 7 时，原式 = 72 + 9×7 + 8 = 120 。