北师大版（2024）七年级下册（2024）3 乘法公式多媒体教学ppt课件

这是一份北师大版（2024）七年级下册（2024）3 乘法公式多媒体教学ppt课件，共17页。PPT课件主要包含了x2–4，1–9a2，4y2–z2，两数的，中间项抵消了，你发现了什么，平方差公式，相同项2-相反项2，a2–22，a2–4等内容，欢迎下载使用。
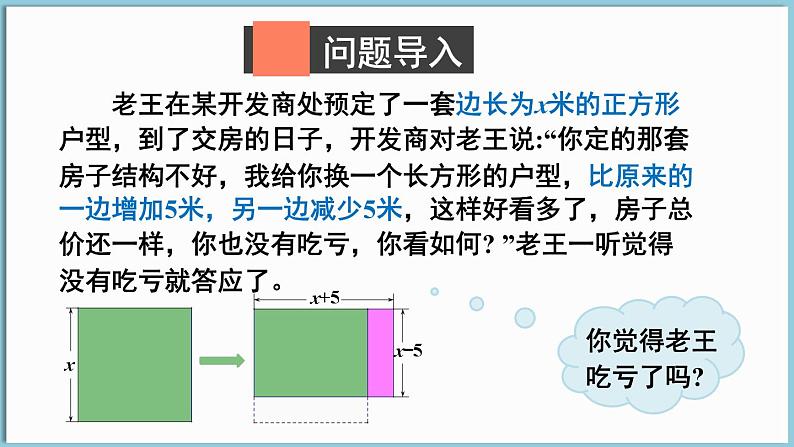
老王在某开发商处预定了一套边长为x米的正方形户型，到了交房的日子，开发商对老王说:“你定的那套房子结构不好，我给你换一个长方形的户型，比原来的一边增加5米，另一边减少5米，这样好看多了，房子总价还一样，你也没有吃亏，你看如何? ”老王一听觉得没有吃亏就答应了。
（1）(x+2) (x–2)
（2）(1+3a)(1–3a)
（3）(x+5y)(1–5y)
（4）(2y+z)(2y–z)
= x2 – 2x + 2x – 4
= 1 – 3a + 3a – 9a2
= x2 – 5xy + 5xy – 25y2
= x2 – 25y2
= 4y2 – 2yz + 2yz – z2
用多项式与多项式相乘的运算法则计算下列多项式的积：
两数_____的___
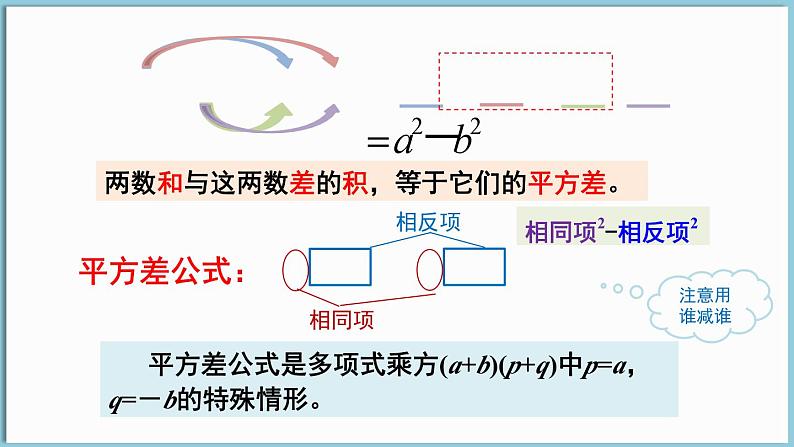
两数和与这两数差的积，等于这两数的平方的差。
你能再举一些类似的例子验证一下你的发现吗?
（1）(3m + 1)(3m - 1); （2）(x2 + y)(x2 - y).
= 9m2 - 3m + 3m - 1=9m2 – 1。
= x4 - x2y + yx2 - y2= x4 - y2。
（1）(3m + 1)(3m - 1)
（2）(x2 + y)(x2 - y)
你能用字母表示你发现的规律吗?
两数和与这两数差的积，等于它们的平方差。
平方差公式是多项式乘方(a+b)(p+q)中p=a，q=－b的特殊情形。
（1）( 5 + 6x ) ( 5 – 6x ) ；
（2） ( x – 2y ) ( x + 2y ) ；
（3） (– m + n ) (– m – n) 。
解：（1）( 5 + 6x ) ( 5 – 6x ) = 52–(6x)2 = 25 – 36x2 ；
（2） ( x – 2y ) ( x + 2y ) = x2– (2y)2 =x2– 4y2；
（3） (– m + n ) (– m – n) = (– m)2 – n2 =m2– n2 。
总结:关键是先确定相同项“a”和相反项“b”。
（1）( a + 2)( a – 2) ； （2）(3a + 2b)(3a – 2b)。
解:（1） ( a + 2)( a – 2)
（2） (3a + 2b)(3a – 2b)
= (3a)2 – (2b)2
= 9a2 – 4b2
例 2 利用平方差公式计算
（2）(ab + 8)(ab – 8) 。
（2）(ab + 8)(ab – 8) = (ab)2 – 82 =a2b2 – 64 。
如何计算(a – b)(– a – b) ?你是怎样做的?
(a – b)(– a – b)= – (a – b) (a + b )= – (a2 – b2)= b2 – a2
注意:对于不能直接应用公式的， 可能要经过变形才可以应用。
（1）(– x –1)(1– x) ； （2）(– 4k + 3)(– 4k – 3)。
解:（1） (– x –1)(1– x)
（2） (– 4k + 3)(– 4k – 3)
= (– x)2 –12
= (– 4k)2 – 32
（1）(an + b)(an – b)
解（1） (an + b)(an – b) = (an)2 – b2 = a2n – b2
（2）(a + 1)(a – 1)(a2 + 1)
（2）(a + 1)(a – 1)(a2 + 1) = (a2 – 1)(a2 + 1) = (a2)2 – 1 = a4 – 1
1. 下列式子能用平方差公式计算吗?① (– 3x + 2)(3x – 2) ② (b + 2a)(2a – b)③ (– x + 2y)(– x – 2y)④ (– x + y)(x – y)
能，4a2 – b2
2.下列多项式中，可以用平方差公式计算的是（ ） A. (2a – 3b)(– 2a+3b) B. (– 3a + 4b)(– 4b – 3a) C. (a – b)(b – a) D. (a – b – c)(– a + b + c)
解析：(– 3a + 4b)(– 4b – 3a) = (– 3a + 4b)(– 3a – 4b) = 9a2 – 16b2
3.下列计算结果正确的是( )A.(x + 2)(x – 2) = x2 – 2B.(x + 2)(3x – 2) = 3x2 – 4C.(ab – c)(ab + c) = a2b2 – c2D.(– x – y)(x + y) = x2 – y2
3x2 + 4x – 4
– x2 – y2 – 2xy
4. 计算（1）(–3x – 7y)(3x – 7y)； （2） (0.2x – 0.3)(0.2x + 0.3)； （3） (mn – 3n) ( mn + 3n)； （4） (– 2x + 3y) (– 2x – 3y)。
解：（1）(–3x – 7y)(3x – 7y)
= (– 7y)2 –(3x)2
= 49 y 2 – 9x 2
（2） (0.2x – 0.3)(0.2x + 0.3)
= (0.2x)2 – (0.3)2
= 0.04x2 –0.09
（3） (mn – 3n) ( mn + 3n)
= (mn)2 – (3n)2
（4） (– 2x + 3y) (– 2x – 3y)
= m2n2 – 9n2
= (– 2x)2– (3y)2