初中数学北师大版（2024）七年级下册（2024）3 乘法公式评课ppt课件

这是一份初中数学北师大版（2024）七年级下册（2024）3 乘法公式评课ppt课件，共16页。PPT课件主要包含了例6计算等内容，欢迎下载使用。
前面我们学习了完全平方公式：
口诀:首平方，尾平方，首尾乘积的2倍放中间。
怎样计算1022，1972更简单呢?
你是怎样做的?与同伴进行交流。
（1）(x+3)2-x2；
（2）(a+b+3) (a+b-3)；
（3）(x+5)2-(x-2)(x-3)；
（4）[(a+b)(a-b)]2。
（1）(x+3)2-x2 =x2+6x+9-x2 =6x+9；
（2）(a+b+3) (a+b-3) = [(a+b)+3][(a+b)-3] = (a+b)2-32 = a2+2ab+b2-9
（4） [(a+b)(a-b)]2 = (a2- b2)2 = a4-2a2b2+b4。
（3）(x+5)2-(x-2)(x-3) = x2+10x+25-(x2-5x+6) = x2+10x+25-x2+5x-6 = 15x+19
利用整式乘法公式计算：
(2) (a-b-3) (a-b+3)
解：962 =(100-4)2 =1002-2×100×4+42 =10000-800+16 =9216
解：(a-b-3) (a-b+3) =(a-b)2-32 =a2-2ab+b2-9
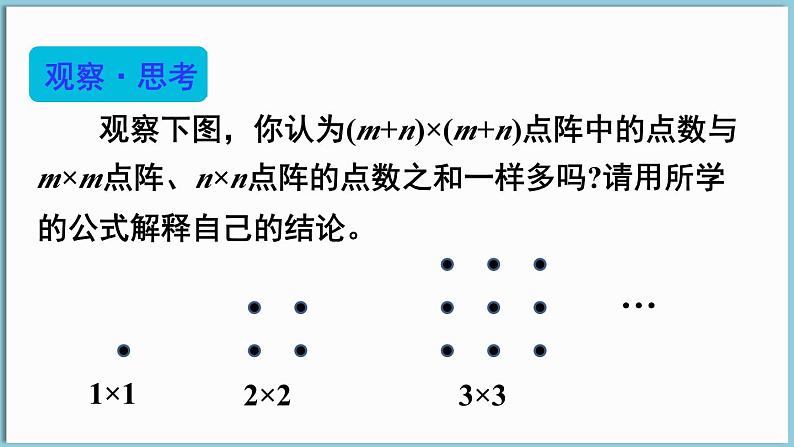
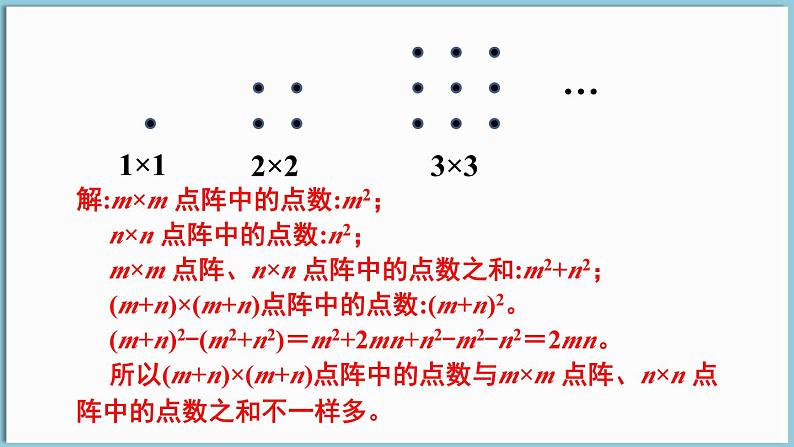
观察下图，你认为(m+n)×(m+n)点阵中的点数与m×m点阵、n×n点阵的点数之和一样多吗?请用所学的公式解释自己的结论。
解:m×m 点阵中的点数:m2； n×n 点阵中的点数:n2； m×m 点阵、n×n 点阵中的点数之和:m2+n2； (m+n)×(m+n)点阵中的点数:(m+n)2。 (m+n)2-(m2+n2)＝m2+2mn+n2-m2-n2＝2mn。 所以(m+n)×(m+n)点阵中的点数与m×m 点阵、n×n 点阵中的点数之和不一样多。
1.若m+n=3，则代数式2m2+4mn+2n2-6的值为（ ） A.12 B.3 C.4 D.0
2.若(a+b)2=49，ab=6，则a-b的值为（ ） A.-5 B.±5 C.5 D.±4
3.已知a=2002x+2003，b=2002x+2004，c=2002x+2005，则多项式2a2+2b2+2c2-2ab-2bc-2ac的值为（ ） A.0 B.2 C.4 D.6
(1)(2x+y+1) (2x+y-1)
解：(2x+y+1) (2x+y-1) =(2x+y)2-12 =4x2+4xy+y2-1
(2)(x-2)(x+2)-(x+1)(x-3)
解：(x-2)(x+2)-(x+1)(x-3) =x2-4-(x2-2x-3) =2x-1
(3)(ab+1)2-(ab-1)2
解：(ab+1)2-(ab-1)2 =a2b2+2ab+1-(a2b2-2ab+1) =a2b2+2ab+1-a2b2+2ab-1 =4ab
(4)(2x-y)2-4(x-y)(x+2y)
解：(2x-y)2-4(x-y)(x+2y) =4x2-4xy+y2-4(x2+2xy-xy-2y2) =4x2-4xy+y2-4x2-4xy+8y2 =9y2-8xy
5.对于依次排列的多项式x+a，x+b，x+c(a，b，c 是常数)，当它们满足(x+b)2 - (x+a)(x+c)=M ，且M 为常数时，则称a，b，c 是一组完美数，M 是该组完美数的完美因子。例如:对于多项式x+1，x+3，x+5，因为(x+3)2 - (x+1)(x+5)=4，所以1，3，5是一组完美数，4是该组完美数的完美因子。试问:当a，b，c 之间满足什么数量关系时，它们是一组完美数? 并说明理由。
解:当2b-a-c=0时，它们是一组完美数。理由:假设a，b，c 是完美数，则(x+b)2- (x+a)(x+c)的结果为常数。(x+b)2- (x+a)(x+c)=x2+2bx+b2- [x2+(a+c)x+ac] =(2b-a-c)x+b2-ac。因为结果为常数，所以2b-a-c=0。