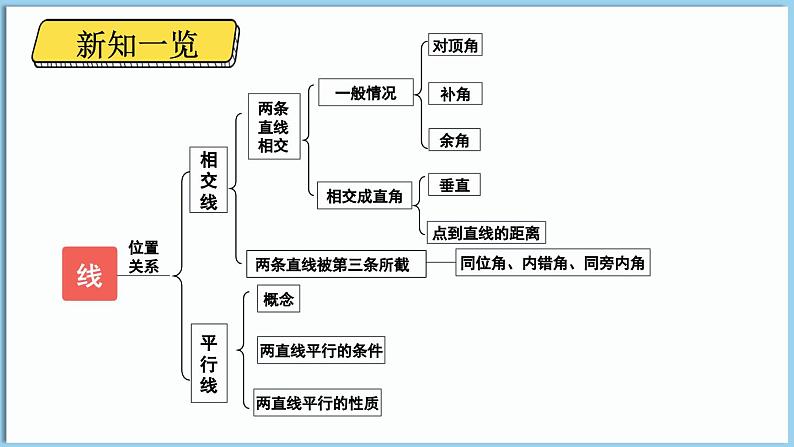
北师大版（2024）七年级下册（2024）第二章 相交线与平行线1 两条直线的位置关系示范课ppt课件

这是一份北师大版（2024）七年级下册（2024）第二章 相交线与平行线1 两条直线的位置关系示范课ppt课件，共23页。PPT课件主要包含了平行线，相交线，OB和OD，OA和OC，OB和OC，OA和OD，∠AOD，∠1∠2，∠3∠4，①②④⑥等内容，欢迎下载使用。
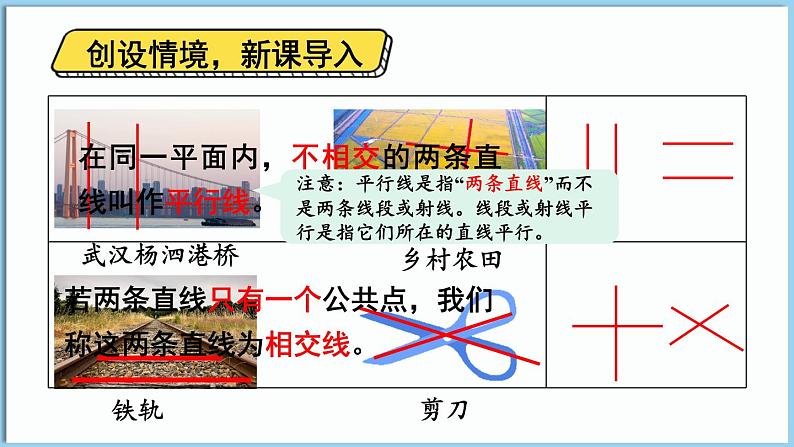
在同一平面内，不相交的两条直线叫作平行线。
若两条直线只有一个公共点，我们称这两条直线为相交线。
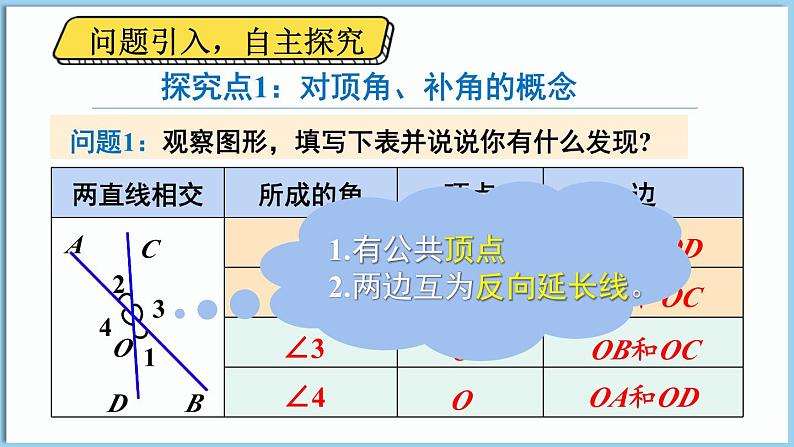
探究点1：对顶角、补角的概念
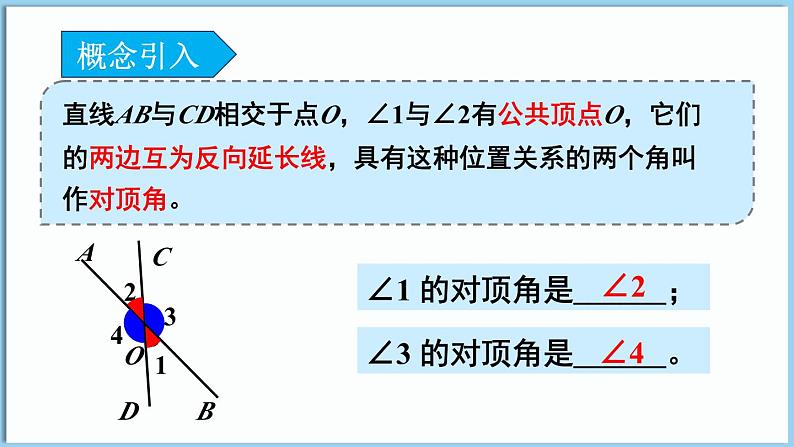
∠1 的对顶角是______；
∠3 的对顶角是______。
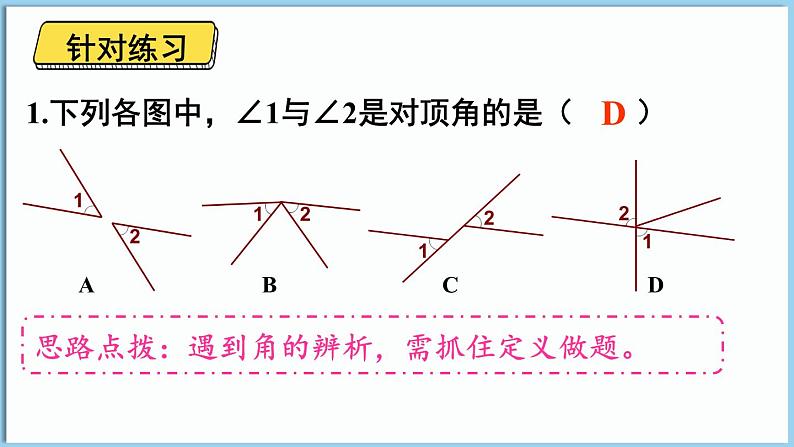
1.下列各图中，∠1与∠2是对顶角的是（ ）
思路点拨：遇到角的辨析，需抓住定义做题。
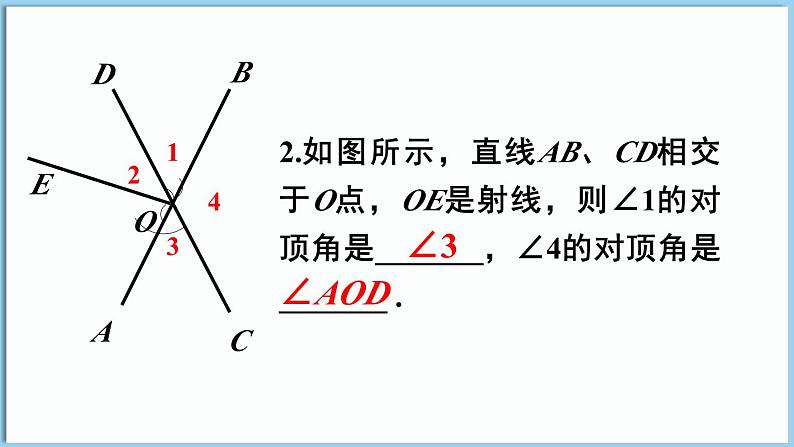
2.如图所示，直线AB、CD相交于O点，OE是射线，则∠1的对顶角是_______，∠4的对顶角是_______ .
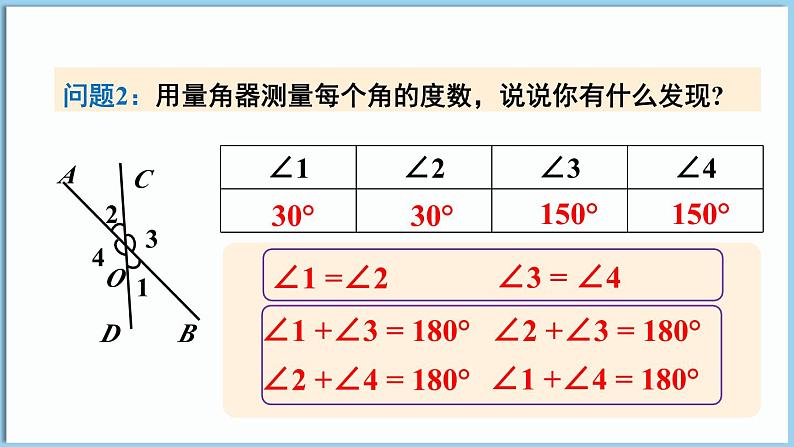
∠1 +∠3 = 180°
∠2 +∠4 = 180°
∠1 +∠4 = 180°
∠2 +∠3 = 180°
∠1 ＋∠2＝90°
下列说法正确的有 ____________（填序号）①已知∠A = 40°，则∠A 的余角等于50°。②若∠1+∠2 = 180°，则∠1和∠2互为补角。③若∠1+∠2+∠3 = 180°，则∠1、∠2、∠3互补。④若∠A = 40°26′，则∠A 的补角=139°34′。⑤一个角的补角必为钝角。⑥一个锐角的补角比这个角的余角大90°。
探究点2：对顶角、补角、余角的性质
方法一：改变角度，测量各个角的度数：
方法二：几何推导证明：
∵ ∠1 +∠3 =180°，∠3 +∠2 =180°，∴ ∠1 =∠2 。
问题4： 如图，打台球时，选择适当的方向用白球击打红球，反弹后的红球会直接入袋，此时，∠1=∠2。
(1)请在右图中找出互为补角和互为余角的角，并说说你的理由。
将上图简化为下图，ON与DC相交所成的∠DON和∠CON都等于90°，且∠1=∠2。
(2)∠3与∠4的大小有什么关系？∠AOC与∠BOD呢？你能说明理由吗？与同伴进行交流。
(1)在右图中找出互为补角和互为余角的角，并说说你的理由。
根据补角和余角的定义知：
∠1和∠3，∠2和∠4
∠DOA和∠ COA ， ∠DON和∠ CON ， ∠DOB和∠ COB 。
(2) ∠3与∠4的大小有什么关系？∠AOC与∠BOD呢？你能说明理由吗？与同伴进行交流。
因为 ∠1+∠3=90°， ∠2+∠4=90°
所以 ∠3=∠4
因为∠AOC=∠AOB+∠BOC
又因为∠BOC =∠AOD
所以 ∠AOC = ∠BOD
∠BOD=∠AOB+∠AOD
1.如图所示，有一个破损的扇形零件，利用图中的量角器可以量出这个扇形零件的圆心角的度数。请指出所量角的度数，并说明理由。
解：根据对顶角的性质可知所量角的度数是40°。
【教材P36 随堂练习 第1题】
2.①因为∠1+∠2=90°，∠2+∠3=90°，所以∠1=____，理由是______________________。② 因为∠1+∠2=180°，∠2+∠3=180°，所以∠1=____，理由是______________________。
3.如图，点O在直线AB上，∠DOC和∠BOE都等于90°。
4.如图，直线AB、CD相交于点O，OE平分∠AOB，OB平分∠DOF，若∠DOE=50°，求∠DOF的度数。
解：因为AB为直线，OE平分∠AOB，所以∠AOE=∠BOE=90°，因为∠DOE=50°，所以∠DOB=40°。因为OB平分∠DOF，所以∠DOB=∠FOB=40°，所以∠DOF=80°。
(1)图中∠AOC的对顶角是________，∠EOB的补角是________。
5.如图，直线AB、CD相交于点O，OE把∠BOD分成两部分。
解：因为∠AOC=70°，所以∠BOD=∠AOC=70°，因为∠BOE∶∠EOD=2∶3，所以∠BOE=28°，所以∠AOE=180°－28°=152°。
（2）若∠AOC=70°，且∠BOE∶∠EOD=2∶3，求∠AOE的度数。