初中数学北师大版（2024）七年级下册（2024）3 平行线的性质示范课ppt课件

这是一份初中数学北师大版（2024）七年级下册（2024）3 平行线的性质示范课ppt课件，共25页。PPT课件主要包含了平行线，相交线，同位角相等，内错角相等，同旁内角互补，两条直线平行，不相等，几何语言，解因为AB∥DC，等量代换等内容，欢迎下载使用。
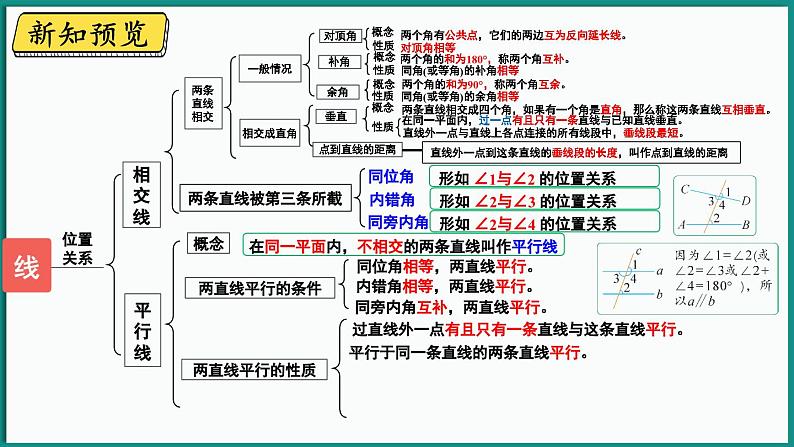
两个角有公共点，它们的两边互为反向延长线。
两个角的和为180°，称两个角互补。
同角(或等角)的补角相等
两个角的和为90°，称两个角互余。
同角(或等角)的余角相等
两条直线相交成四个角，如果有一个角是直角，那么称这两条直线互相垂直。
在同一平面内，过一点有且只有一条直线与已知直线垂直。
直线外一点与直线上各点连接的所有线段中，垂线段最短。
直线外一点到这条直线的垂线段的长度，叫作点到直线的距离
同位角相等，两直线平行。
过直线外一点有且只有一条直线与这条直线平行。
平行于同一条直线的两条直线平行。
内错角相等，两直线平行。
同旁内角互补，两直线平行。
回顾：三种平行线的判定方法分别是什么?
在两条直线平行的条件下，同位角、内错角、同旁内角又各有什么关系呢？
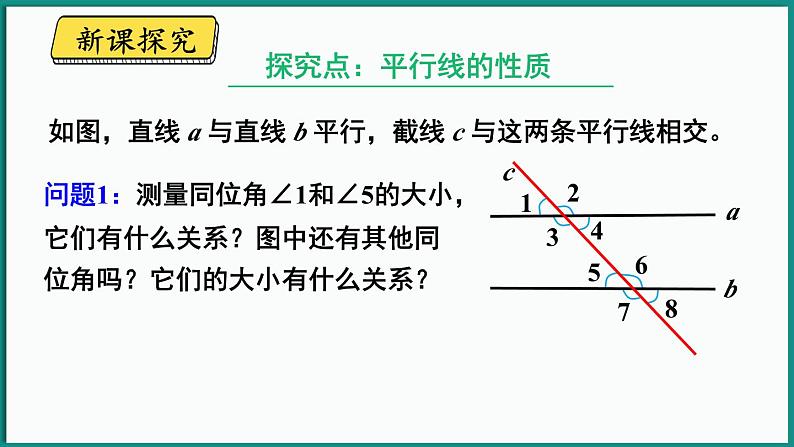
如图，直线 a 与直线 b 平行，截线 c 与这两条平行线相交。
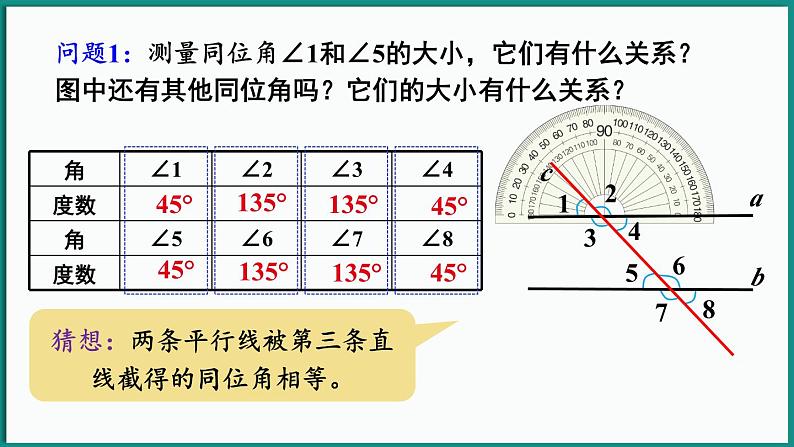
问题1：测量同位角∠1和∠5的大小，它们有什么关系？图中还有其他同位角吗？它们的大小有什么关系？
猜想：两条平行线被第三条直线截得的同位角相等。
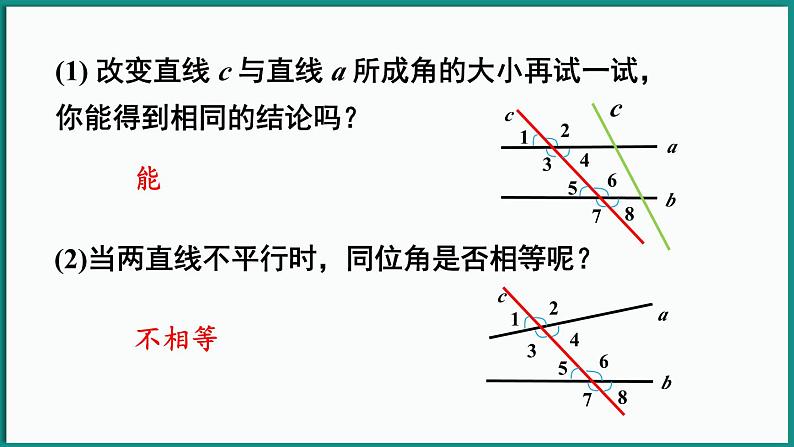
(1) 改变直线 c 与直线 a 所成角的大小再试一试，你能得到相同的结论吗？
(2)当两直线不平行时，同位角是否相等呢？
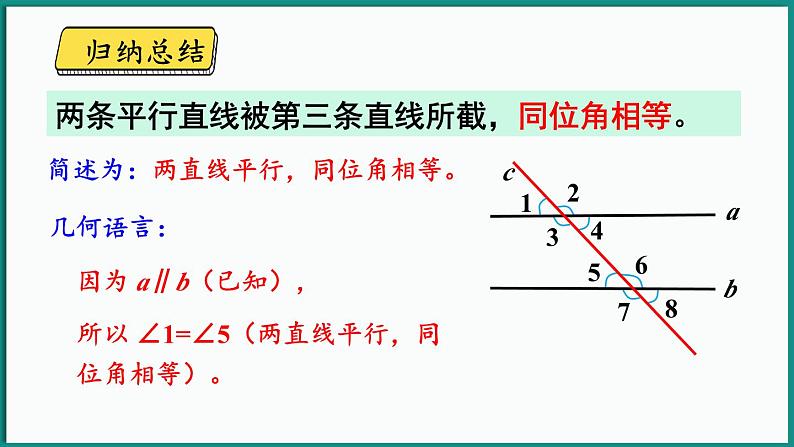
两条平行直线被第三条直线所截，同位角相等。
简述为：两直线平行，同位角相等。
因为 a∥b（已知），
所以 ∠1=∠5（两直线平行，同位角相等）。
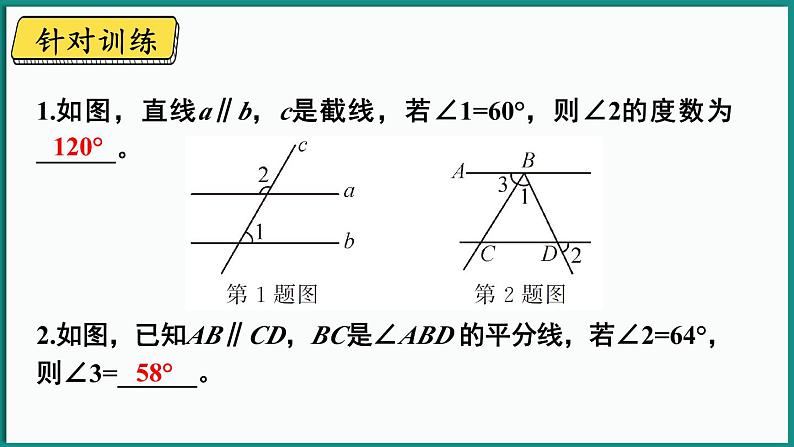
1.如图，直线a∥b，c是截线，若∠1=60°，则∠2的度数为______。
2.如图，已知AB∥CD，BC是∠ABD 的平分线，若∠2=64°，则∠3=______。
猜想：两条平行线被第三条直线截得的内错角相等。
问题2：图中有几对内错角？它们的大小有什么关系？为什么？
你能结合图形，推出两条平行线被第三条直线截得的内错角之间的关系吗？
解：因为a∥b (已知)，
所以∠1=∠5 (两直线平行，同位角相等)。
又因为∠1=∠4 (对顶角相等)，
所以∠4=∠5 (等量代换)。
两条平行直线被第三条直线所截，内错角相等。
简述为：两直线平行，内错角相等。
因为 a∥b (已知)，
所以 ∠3=∠6 (两直线平行，内错角相等)。
1.如图，AB∥CD，如果∠B=35°，那么∠C的度数为( )。A.25°B.30°C.35°D.55°
2.如图，平行线AB，CD被直线EF所截，FG平分∠EFD，若∠EFD=70°，则∠EGF的度数是______。
猜想：两条平行线被第三条直线截得的同旁内角互补。
问题3：图中有几对同旁内角？它们的大小有什么关系？为什么？
结合图形，尝试写出推理的过程。
解：因为a∥b (已知)，
又因为∠1+∠3=180° (平角的定义)，
所以∠5+∠3=180°(等量代换)。
两条平行直线被第三条直线所截，同旁内角互补。
简述为：两直线平行，同旁内角互补。
因为 a∥b (已知)，
所以 ∠3+∠5=180°(两直线平行，同旁内角互补)。
如图是一块梯形铁片的残余部分，量得∠A =100°，∠B=115°，梯形的另外两个角分别是多少度?
所以∠A+∠D=180°，∠B+∠C =180°(两直线平行，同旁内角互补)。
又因为∠A=100°，∠B=115°，
所以∠D=180°－∠A=180°－100°=80°，
∠C=180°－∠B=180°－115°=65°。
答：梯形的另外两个角分别是 80°和65°。
如图，一束平行光线AB与DE射向一个水平镜面后被反射，此时∠1=∠2，∠3=∠4。
(2) 反射光线 BC 与 EF 也平行吗？
(1)∠1 与∠3 的大小有什么关系？∠2 与∠4 呢？
下面是小颖的思路，你能说明小颖每一步的理由吗？
(1)由于AB∥DE，可以得到∠1=∠3；由∠1=∠2， ∠3=∠4，可以得到∠2=∠4。
(2) 由∠2=∠4，可以得到BC∥EF。
(1)由于 AB∥DE，可以得到 ∠1=∠3；
(两直线平行，同位角相等)
由∠1=∠2， ∠3=∠4，可以得到∠2=∠4
(同位角相等，两直线平行)
1.如图，AB//CD，AC//BD， 分别找出与∠1相等或互补的角。
【教材P50 随堂练习 第1题】
∠2、∠3、∠4及其对顶角，∠1的对顶角。
∠5、∠6、∠7、∠8及其对顶角。
2.如图，AB//CD， ∠α=45°，∠D=∠C， 依次求出∠D，∠C，∠B的度数。
∠D= ∠α =45°，
∠C= ∠D =45°，
（两直线平行，同位角相等）
（两直线平行，同旁内角互补）
∠B=180°- 45°=135°。
3.如图，AB//CD， CD//EF， ∠1=∠2=60°，∠A和∠E 各是多少度？它们相等吗？
因为 AB//CD， CD//EF，
所以 ∠1+∠A=180°， ∠2+∠E=180°。
又因为 ∠1=∠2=60°，
所以 ∠A = ∠ E =180°- 60°=120°。
4.如图，从一艘船上测得一个灯塔的方向是北偏西48°，那么这艘船在这个灯塔的什么方向？
由两直线平行内错角相等可得这艘船在这个灯塔南偏东48°。
5.如图，直线a // b，∠1=54°，∠2，∠3，∠4各是多少度？
解：因为 a∥b，∠1=54°，所以 ∠4 =∠1 = 54°(两直线平行，同位角相等)，∠3 =180°－∠4=180° － 54°=126°。因为 ∠2 与∠1 是对顶角，所以∠2=∠1= 54°。
6. 光线在不同介质中的传播速度是不同的，因此当光线从水中射向空气时，要发生折射，由于折射率相同，所以在水中平行的光线，在空气中也是平行的。如图，∠1＝45°，∠2＝122°，求图中其他角的度数。
解：由题意得： ∠3 =∠1 = 45°，∠1+∠7 = 180°，所以 ∠7 = 180°－∠1 = 135°，所以 ∠8 =∠7 = 135°。因为 ∠4 =∠2 = 122°，∠2 +∠5 = 180°，所以 ∠5 = 180°－∠2 = 58°，所以 ∠6=∠5=58°。