北师大版（2024）七年级下册（2024）2 简单的轴对称图形教学课件ppt

这是一份北师大版（2024）七年级下册（2024）2 简单的轴对称图形教学课件ppt，共22页。PPT课件主要包含了所以CDCD，几何语言，垂直平分线，作直线CD等内容，欢迎下载使用。
1.什么样的图形叫作轴对称图形?
如果一个平面图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫作轴对称图形。
3.线段是轴对称图形吗?
线段AB是轴对称图形吗?
如果是，请描述它的对称轴的特点?
线段AB是轴对称图形。
对称轴垂直且平分线段AB。
探究点1：线段垂直平分线的性质
垂直于一条线段， 并且平分这条线段的直线， 叫作这条线段的垂直平分线(简称“中垂线”)。
线段垂直平分线的定义:
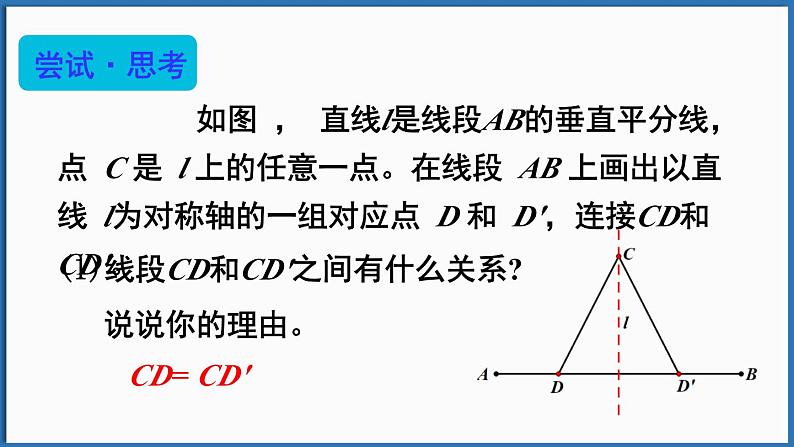
如图 ， 直线l是线段AB的垂直平分线，点 C 是 l 上的任意一点。在线段 AB 上画出以直线 l为对称轴的一组对应点 D 和 D'，连接CD和CD'。
线段CD和CD'之间有什么关系? 说说你的理由。
因为点D和D'关于对称轴 l 对称，交线段AB于点E，
所以DE= D'E，∠CED=∠CED'。
在△CED和△CED'中，
因为DE= D'E，∠CED=∠CED'，CE=CE。
所以△CED≌△CED'(SAS)
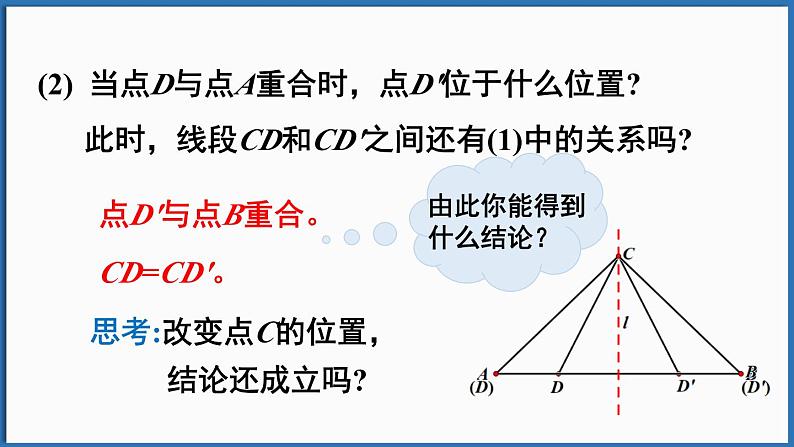
(2) 当点D与点A重合时，点D'位于什么位置? 此时，线段CD和CD'之间还有(1)中的关系吗?
思考:改变点C的位置， 结论还成立吗?
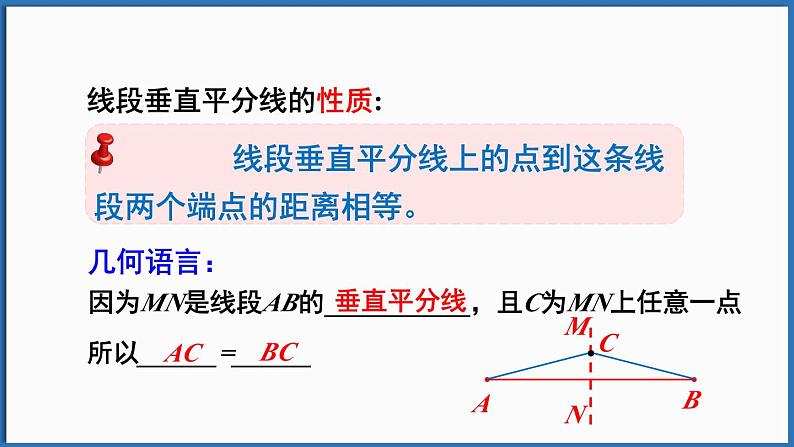
线段垂直平分线的性质:
因为MN是线段AB的___________，且C为MN上任意一点
所以______=______
1.如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，连接AE。若BC=6，AC= 5，则△ACE的周长为( )
A. 8B. 11C. 16D. 17
线段垂直平分线的判定:
2.如图，己知AB是线段CD上的垂直平分线，E是AB上的一点，如果EC=7cm，那么ED的长是多少?
解：ED的长是7cm。
如图，已知线段AB，如何作出它的垂直平分线?
思路2：①确定垂直平分线上的两个点；②连接两点确定垂直平分线。
思路1：①确定线段AB的中点；②过线段AB的中点作它的垂线。
探究点2：线段的垂直平分线的作法
假设线段AB的垂直平分线已作出，那么
(1) 这条直线有什么特征?
(2) 如何确定这条直线上的两个点?
这条直线与AB的交点是AB的中点，且与AB垂直，直线上的点到线段AB两端距离相等。
提示：需要确定的点是线段对称轴上的点，因此应当从线段两端进行“对称”的操作。
例　如图，已知线段 AB，请用尺规作线段 AB 的垂直平分线。
如图，已知直线l 和l 上的一点P，如何用尺规作l 的垂线，使它经过点P? 能说明你的作法的道理吗?
1.以P点为圆心，以任意长为半径画圆，交 l 于A、B两点；
直线CD即为过点P 的直线l 的垂线。
如图，直线 m 表示小区内的一条柏油马路，A，B表示两栋住宅楼，要在柏油马路旁边建一个智能垃圾分类投放点P，使智能垃圾分类投放点到两栋住宅楼的距离相等。你认为智能垃圾分类投放点P应该修在什么位置?
1.如图，在△ABC中，BC=8cm，边AB的垂直平分线交AB于点D，交边AC于点E，△BCE的周长等于18cm，则AC的长是_______。
2. 在△ABC中，AB的中垂线与AC边所在直线相交所得的锐角为50°，则∠A的度数为（ ）
A.50° B.40°C.40°或 140° D.40°或 50°
3.如图，在△ABC中，BC=8，AB的垂直平分线交BC于D，AC的垂直平分线交BC于E，则△ADE的周长等于______。
4.如图，在△ABC 中，AF 平分∠BAC，AC 的垂直平分线DE分别交AC，BC 于点 D，E，连接AE，∠B=70°∠FAE=19°，则∠C的度数为______。