【湘教版】七下数学 第一章 整式的乘法 小结与评价（课件+教案）

这是一份【湘教版】七下数学 第一章 整式的乘法 小结与评价（课件+教案），文件包含小结与评价pptx、章末复习doc等2份课件配套教学资源，其中PPT共29页， 欢迎下载使用。
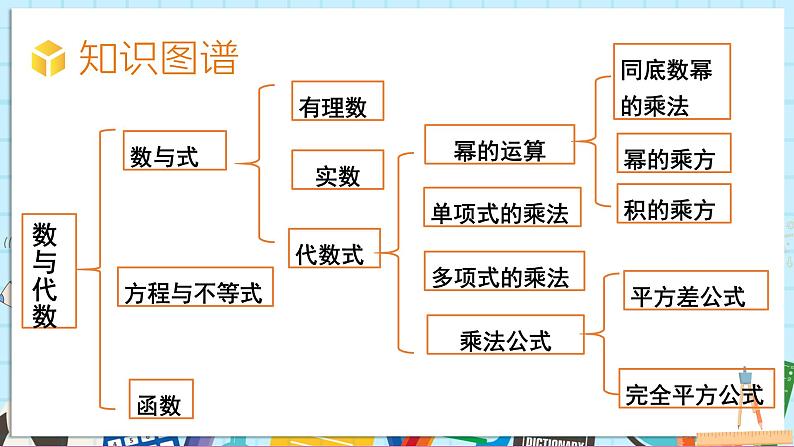
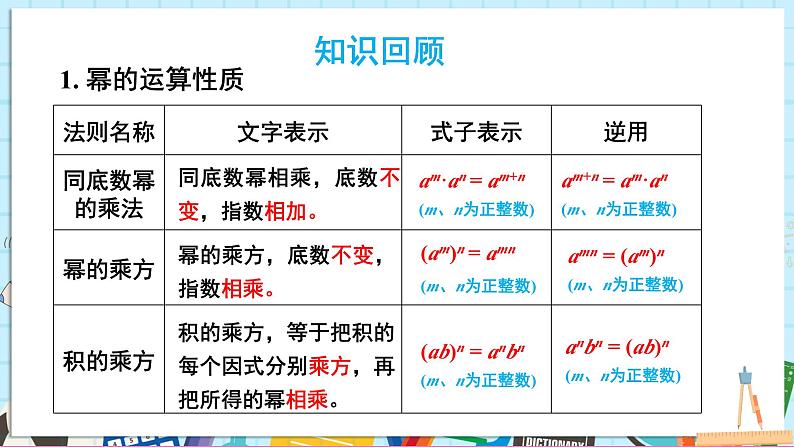
湘教版数学七年级下册第一章 整式的乘法小结与评价数与代数数与式方程与不等式函数有理数实数代数式幂的运算单项式的乘法多项式的乘法乘法公式同底数幂的乘法幂的乘方积的乘方平方差公式完全平方公式1. am·an,(am)n,(ab)n(m,n是正整数)应分别怎么计算?2.单项式与单项式相乘，怎么乘?单项式与多项式相乘呢?多项式与多项式相乘呢?3.叙述平方差公式，并解释几何背景。4.叙述完全平方公式，并解释几何背景。am·an = am+n(m、n为正整数)am+n = am·an(m、n为正整数)(am)n = amn(m、n为正整数)amn = (am)n(m、n为正整数)(ab)n = anbn(m、n为正整数)anbn = (ab)n(m、n为正整数)知识回顾同底数幂相乘，底数不变，指数相加。幂的乘方，底数不变，指数相乘。积的乘方，等于把积的每个因式分别乘方，再把所得的幂相乘。1. 幂的运算性质2.整式的乘法：(1)单项式乘单项式： 法则：单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，其余的字母连同它的指数不变，作为积的因式.2.整式的乘法：(2)单项式乘多项式：m(a + b + c) = ma + mb + mc 法则：单项式与多项式相乘，就是根据分配律用单项式去乘多项式的每一项，再把所得的积相加.2.整式的乘法：(3)多项式乘多项式：(a + b)(m + n) = am + an + bm + bn 多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加.两数和与这两数的差的积，等于这两数的平方的差。(a+b)(a-b) = a²- b²两数和(差)的平方，等于这两数的平方和加上(减去)这两数积的2倍。(a±b)2 =a²±2ab+b²a² = (a+b)(a-b) + b²b² = a² - (a+b)(a-b)a² + b² = (a+b)2 -2ab或a² + b² = (a-b)2 +2ab (a+b)2 =(a-b)2 +4ab 3. 乘法公式：1.同底数幂的乘法和幂的乘方容易混淆，进行运算时要注意区分。2.多项式与多项式相乘，要用一个多项式的每一项分别乘另一个多项式的每一项，注意不要漏乘。3.平方差公式和完全平方公式都是多项式乘法的重要公式，其中的字母x，y可以用任何数或者任意多项式代入。典例精析1.下列运算正确的是 ( ) A. x3+x3 = x6 B. 2x·3x2 = 6x3 C. (2x)3 = 6x3 D. (2x2+x)÷x = 2x解析：A.应为 x3 + x3 = 2x3,故本选项错误；B. 2x · 3x2 = 6x3, 正确；C.应为(2x)3 = 23x3 = 8x3,故本选项错误；D.应为 (2x2 + x)÷x = 2x + 1，故本选项错误.B2.已知 a=8131,b=2741,c=961,则 a,b,c 的大小关系是 ( ) A. a>b>c B. a>c>b C. aa解析：因为a = 8131 = (34)31 = 3124; b = 2741 = (33)41 = 3123;c = 961 = (32)61 = 3122. 则 a > b > c. 故选 A.A3. 一个长方体的长、宽、高分别 3a-4, 2a, a, 它的体积等于（ ） A. 3a3-4a2 B. a2 C. 6a3-8a2 D. 6a3-8a解析：由题意知，V长方形 = (3a-4)·2a·a=6a3-8a2.故选 C.C4. 已知：2x = 4y+1, 27y = 3x-1, 则 x-y =______.35. 计算：（1）82×42010×(-0.25)2014;解：82×42010×(-0.25)2014 = 43×42010×(-0.25)2014 = 42013×(-0.25)2013×(-0.25) = -0.25× (-4×0.25)2013 = 0.255. 计算：（2）20142 - 2013×2015.解：20142 - 2013×2015 = 20142 - (2014 -1)(2014 + 1) = 20142-(20142 - 12) = 20142 - 20142 + 1 = 16. 先化简，再求值：(a2b-2ab2-b3)÷b-(a+b)(a-b),其中 a = , b = -1.解： (a2b-2ab2-b3)÷b-(a+b)(a-b) = a2-2ab-b2-(a2-b2) = a2-2ab-b2-a2+b2 = -2ab当 a = , b = -1 时，原式 = -2× ×(-1) = 1.7. 若 (x+y)2 = 36 , (x-y)2 = 16 ,求 xy、x2 + y2 的值.解：因为 (x+y)2 = 36 , (x-y)2 = 16， 所以 x2 + 2xy + y2 = 36 ①，x2 - 2xy + y2 = 16 ②,①-② 得 4xy = 20, 所以 xy = 5,①+② 得 2(x2+y2) = 52,所以 x2+y2 = 26.巩固提高1.已知：a+b=m，ab=-4，化简：(a-2)(b-2) 的结果是( ) A. 6 B. 2m-8 C. 2m D. -2m解析：因为a+b = m，ab = -4，所以 (a-2)(b-2) = ab + 4-2(a+b) = -4+4-2m = -2m. 故选D.D2. 某商场四月份售出某品牌衬衣 b 件，每件 c 元，营业额a 元. 五月份采取促销活动，售出该品牌衬衣 3b 件，每件打八折，则五月份该品牌衬衣的营业额比四月份增加( ) A. 1.4a 元 B. 2.4a 元 C. 3.4a 元 D. 4.4a 元解析：5月份营业额为4月份营业额为 a, 所以 a-a = 1.4a.A3. 已知 (x+a)(x+b) = x2-13x + 36，则 a + b 的值是 ( ) A. 13 B. -13 C. 36 D. -36解：(x + a)(x + b) = x2 + (a+b)x + ab，又因为(x + a)(x + b) = x2-13x + 36，所以 a+b = -13. 故选B.B4. 若 (a+2)2 + | b+1| = 0，则 5ab2 –{2a2b-[3ab2-(4ab2-2a2b)]} = ______.解析：由 (a+2)2 + | b+1 | = 0 得a = -2, b = -1, 当 a = -2, b = -1 时，5ab2 – {2a2b - [3ab2 - (4ab2 - 2a2b)]} = 4ab2 = -8. -85. 计算：解：根据幂的乘方与积的乘方法则可知， 原式 = 6. 已知 ，求 的值.解：因为 = 4， 所以 + 2 = 16， 所以 = 14. 7. 先化简：(2x-1)2 - (3x+1)(3x-1) + 5x(x-1), 再选取一个你喜欢的数代替 x 求值.解：(2x - 1)2 - (3x + 1)(3x - 1) + 5x(x - 1) = 4x2 - 4x + 1 - (9x2 - 1) + 5x2 - 5x = 4x2 - 4x + 1 - 9x2 + 1 + 5x2 - 5x = -9x + 2取x=13，原式=-9×13+2=-115.(求值答案不唯一)通过本章的学习，你对以下几个方面的学习内容掌握得怎么样?根据自己的学习情况，点亮属于你的小星星，然后请同学和老师对你的自评进行恰当的评价。请完成下面两项评价，先自评再在小组内进行互相评价。其中评价由低到高分为1，2，3，4，5五个等级.你对本章的学习及评价还满意吗?新学期会学习新知识,也一定会有新的挑战，但只要保持积极认真的学习态度;不断思考,不断积累,不断总结，就一定能获得更大的进步!课堂小结1.从课后习题中选取；2.完成练习册本课时的习题.课后作业