中职数学高教版（2021）拓展模块二 下册6.4.2 正弦定理教课内容课件ppt

这是一份中职数学高教版（2021）拓展模块二 下册6.4.2 正弦定理教课内容课件ppt，共24页。PPT课件主要包含了教学目标，教学重难点，情境1，建立数学模型，如何求AC的距离，情境2，正弦定理，解三角形，正弦定理的发展史，小组合作等内容，欢迎下载使用。
2024年10月30日4时27分，神舟十九号载人飞船搭载三名航天员，由长征二号F遥十九火箭从我国酒泉卫星发射中心发射升空，约10分钟后，神舟十九号载人飞船与火箭成功分离，进入预定轨道，航天员乘组状态良好，发射取得圆满成功。此次任务是我国空间站应用与发展阶段第4次载人飞行任务，也是我国载人航天工程第33次飞行任务。
卫星距离我们到底有多远呢？能用我们所学知识进行估算吗？
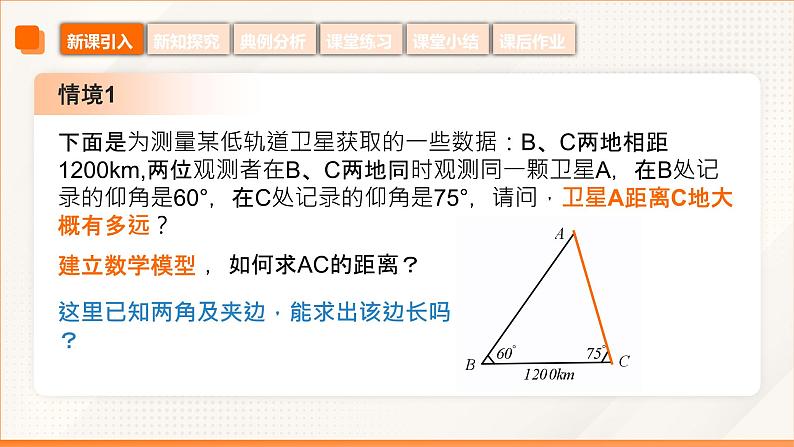
下面是为测量某低轨道卫星获取的一些数据：B、C两地相距1200km,两位观测者在B、C两地同时观测同一颗卫星A，在B处记录的仰角是60°，在C处记录的仰角是75°，请问，卫星A距离C地大概有多远？
这里已知两角及夹边，能求出该边长吗？
月球是地球的自然卫星，了解月球与地球之间的距离对于天文学和航天工程等领域至关重要。
地面上的科学家，只要对准月球的相应位置发射一束强激光束，就能收到镜面反射回来的峰值，根据激光来回的时间，就能精确测量地月距离。
求地月距离转化成求三角形的边长的问题
即 bsinA= asinB．
在一个三角形中，各边与其所对角的正弦之比相等．
即，在任意△ABC中，都有
已知两角和任一边，求其他的边和角；已知两边和其中一边的对角，求其他边和角；边角互相转化。
在三角形中，根据任意三角形的已知边、角，计算未知边、角的过程，叫做解三角形。
注意： 三角形的三角和为180°，确保计算的角度在0°到180°之间，这是三角形内角的可能范围．
►最早是阿拉伯的数学家阿布尔提出了平面三角的正弦定理.
►1030年数学家阿尔毕鲁尼首次对定理进行了证明.
►1464年德国数学家雷格蒙塔努斯在他的著作《论各种三角形》中清晰地将定理展示出来.
►在后来很漫长的一段时间，人们才慢慢地接受并应用正弦定理.
在△ABC中，∠B=45°，∠C=15°，a=5，求b．  
在△ABC中，由∠A+∠B+∠C=180°，
得∠A=180°-∠B-∠C =180°-45°-15°=120°．
又因为0°