初中数学北师大版（2024）九年级下册3 三角函数的计算同步练习题

这是一份初中数学北师大版（2024）九年级下册3 三角函数的计算同步练习题，共13页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．利用科学计算器计算，下列按键顺序正确的是（ ）
A．
B．
C．
D．
2．如图，在△ABC中，点E在AC上，点G在BC上，连接EG，AE=EG=5，过点E作ED⊥AB，垂足为D，过点G作GF⊥AC，垂足为F，此时恰有DE=GF=4．若BG=2，则sinB的值为（ ）
A．B．C．D．
3．在△ABC中，锐角A、B满足|sinA-|+[cs（B-15°）-]2=0，则△ABC是（ ）
A．等腰三角形B．直角三角形
C．等腰直角三角形D．无法确定
4．在锐角中，，则的度数是（ ）
A．B．C．D．
5．下列命题正确的是（ ）
A．若锐角满足，则
B．在平面直角坐标系中，点关于轴的对称点为
C．两条直线被第三条直线所截，同旁内角互补
D．相似三角形周长之比与面积之比一定相等
6．已知为锐角，，则等于（ ）
A．B．C．D．
7．利用科学计算器计算2sin 50°，下列按键顺序正确的是（ ）
A． 2 sin 5 0 =B．2 sin 5 0 =
C． 2 5 0 sin =D．2 5 0 sin =
8．式子sin45°+sin60°﹣2tan45°的值是（ ）
A．22B．C．2D．2
9．在Rt△ABC中，∠C=90°，若sinA=，则csA的值为（ ）
A．B．C．D．
10．如图，在矩形按以下步骤作图：①分别以点和为圆心，以大于的长为半径作弧，两弧相交于点和；②作直线交于点；③连接，．若，，则的度数为（ ）
A．B．C．D．
11．在△ABC中，（3tanA-3）2+=0，则△ABC为( )
A．直角三角形B．等边三角形
C．含60°的任意三角形D．是底角为30°的等腰三角形
12．计算（-）÷×cs60°-20150的结果是（ ）
A．B．C．D．
二、填空题
13．如图，四边形ABCD是矩形，，，以点A为圆心，AB长为半径画弧，交CD于点E，交AD的延长线于点F，则图中阴影部分的面积是 ．
14．计算： ．
15．计算：（-3）2×+（sin45°-1）0-（）-1+= ．
16．计算： ．
17．如图，已知四边形是平行四边形，，将它沿翻折得到四边形，若四边形是正方形，则的度数是 ．

三、解答题
18．（1）计算：；
（2）求值：已知，求的值；
（3）解方程：．
19．尺规作图（用圆规和直尺作图，不写过程，但要保留作图痕迹）
已知，如图，线段，利用无刻度的直尺和圆规，在线段的上方作一个满足条件的，使得：①为直角；②．
20．（1）计算：；
（2）《周髀算经》中记载了“偃矩以望高”的方法．“矩”在古代指两条边呈直角的曲尺（即图中的），“偃矩以望高”的意思是把“矩”仰立放，可测量物体的高度．如图，点A，B，Q在同一水平线上，和均为直角，与相交于点D．测得，，，求树高．
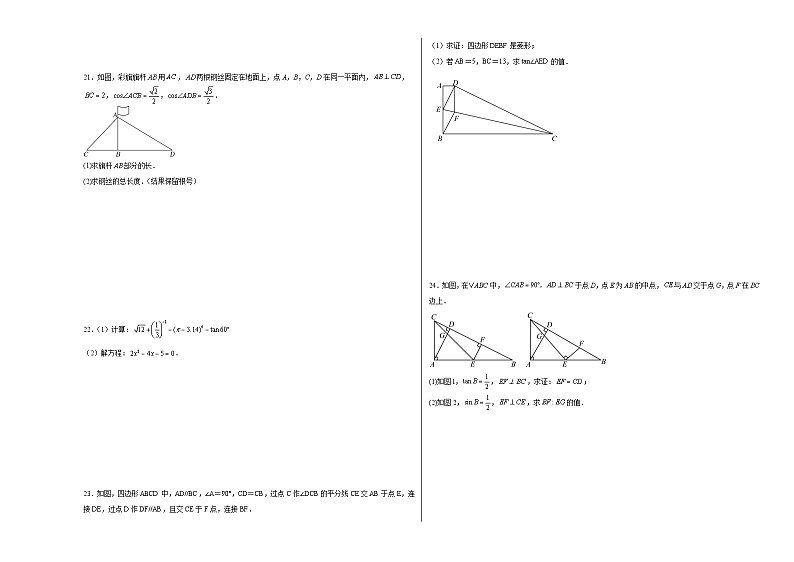
21．如图，彩旗旗杆用，两根钢丝固定在地面上，点A，B，C，D在同一平面内，，，，．
(1)求旗杆部分的长．
(2)求钢丝的总长度．（结果保留根号）
22．（1）计算：
（2）解方程：．
23．如图，四边形ABCD中，AD//BC，∠A＝90°，CD＝CB，过点C作∠DCB的平分线CE交AB于点E，连接DE，过点D作DF//AB，且交CE于F点，连接BF．
（1）求证：四边形DEBF是菱形；
（2）若AB＝5，BC＝13，求tan∠AED的值．
24．如图，在中，于点D，点E为的中点，与交于点G，点F在边上．

(1)如图l，，，求证：；
(2)如图2，，，求的值．
《1.3三角函数的计算》参考答案
1．A
【分析】简单的电子计算器工作顺序是先输入者先算，根据按键顺序写出式子，再根据开方运算即可求出显示的结果．
【详解】
解：利用该型号计算器计算 ，按键顺序正确的是：

故选：A．
【点睛】本题主要考查了计算器-三角函数，要求学生对计算器上的各个功能键熟练掌握，会根据按键顺序列出所要计算的式子．借助计算器这样的工具做题既锻炼了学生动手能力，又提高了学生学习的兴趣．
2．C
【详解】试题分析：在Rt△ADE与Rt△EFG中，
∴Rt△ADE≌Rt△EFG（HL）．
∴∠A=∠GEF．
∵∠A+∠AED=90°，
∴∠GEF+∠AED=90°，
∴∠DEG=90°．
如图，过点G作GH⊥AB于点H，则四边形DEGH为矩形，
∴GH=DE=4．
在Rt△BGH中，sinB=．
故选C．
考点：1.矩形的判定与性质；2.全等三角形的判定与性质；3.锐角三角函数的定义．
3．C
【分析】根据非负数的性质求出sinA和cs（B-15°）的值，然后求出∠A和∠B的度数，即可判断△ABC的形状．
【详解】∵|sinA-|+[cs（B-15°）-]2=0，
∴，且，
∴sinA=，
∴∠A=45°，
∵，
∴cs（B-15°）=，
∴∠B-15°=30°，
∴∠B=45°，
∴∠C=90°，
∴△ABC为等腰直角三角形，
故选：C．
【点睛】本题考查了特殊角的三角函数值，解答本题的关键是掌握几个特殊角的三角函数值．
4．D
【分析】本题考查了非负数的性质，特殊角的三角函数，三角形内角和定理等知识，先根据非负数的性质求出，，然后根据特殊角的三角函数求出，，最后根据三角形内角和定理求解即可．
【详解】解∶∵，
∴，，
∴，，
∴，
故选∶D．
5．B
【分析】利用特殊角的三角函数值，可对A作出判断；利用关于x轴对称的点的坐标特点：横坐标不变，纵坐标互为相反数，可对B作出判断；利用平行线的性质，可对C作出判断；利用相似三角形的面积比等于周长比的平方，可对D作出判断．
【详解】A. 若锐角满足，则，错误；
B. 在平面直角坐标系中，点关于轴的对称点为，正确；
C. 两条平行直线被第三条直线所截，同旁内角互补，错误；
D. 相似三角形面积之比等于周长之比的平方，错误；
故答案为：B.
【点睛】本题考查常见的一些易错的知识点，注意对概念的准确掌握．
6．A
【分析】本题考查了特殊角的三角函数值，熟记特殊的三角函数值是解题的关键．
先求出然后计算的值．
【详解】解：，
∴，
∵是锐角，
∴，
∴．
故选：A ．
7．A
【解析】略
8．B
【分析】先分别求解特殊角的三角函数值，再代入运算式进行计算即可.
【详解】解：sin45°+sin60°﹣2tan45°



故选B
【点睛】本题考查的是特殊角的三角函数值的混合运算，正确的记忆特殊角的三角函数值是解本题的关键.
9．D
【详解】方法一：根据同一锐角的正弦与余弦的平方和是1，解：∵sin2A+cs2A=1，即（）2+cs2A=1，∴cs2A=，∴csA=或﹣（舍去），∴csA=．故选D．
方法二：根据正弦、余弦函数的定义求解，解：画Rt△ABC，∠A的对边为5，斜边为13，根据勾股定理求出邻边为12，邻边与斜边的比值就是csA=．故选D．
10．D
【分析】利用ED、CD的长度在Rt△ECD中求出∠DEC=60°，即有∠EAC+∠ECA=∠DEC=60°，再根据MN是线段AC的垂直平分线，得出AE=EC，继而得出∠EAC=∠ECA，则有∠EAC=30°，再根据，得到∠EAC=∠ACB，即有∠ACB=30°．
【详解】在Rt△ECD中，tan∠ECD=，
∴∠ECD=30°，
又∵∠EDC=90°，
∴∠DEC=60°，
∴∠EAC+∠ECA=∠DEC=60°，
据图可知，MN是线段AC的垂直平分线，
∴AE=EC，
∴∠EAC=∠ECA，
∴∠EAC=30°，
在矩形ABCD中，，
∴∠EAC=∠ACB，
∴∠ACB=30°．
故选：D．
【点睛】本题考查了垂直平分线的性质、用锐角三角函数解直角三角形等知识，利用三角函数解出∠DEC是解答本题的关键．
11．A
【分析】先根据非负数的性质得出tanA与csB的值，再由特殊角的三角函数值求出∠A与∠B的值，进而可得出结论．
【详解】∵（3tanA-3）2+=0，
∴3tanA-3=0，2csB-3=0，
∴tanA=3，csB=，
∴∠A=60°，∠B=30°，
∴△ABC是直角三角形．
故选A．
【点睛】本题考查的是特殊角的三角函数值，熟记各特殊角度的三角函数值是解答此题的关键．
12．B
【详解】试题分析：原式利用特殊角的三角函数值，零指数幂法则，以及乘除运算法则计算即可得到结果．
试题解析：原式=-
=，
故选B．
考点：1．实数的运算；2．零指数幂；3．特殊角的三角函数值．
13．．
【分析】根据题意可以求得和的度数，然后根据图形可知阴影部分的面积就是矩形的面积与矩形中间空白部分的面积之差再加上扇形EAF与的面积之差的和，本题得以解决．
【详解】解：连接AE，
∵，，，
∴，
∴，
∴，，
∴，
∴阴影部分的面积是：，
故答案为．
【点睛】本题考查扇形面积的计算、矩形的性质，解答本题的关键是明确题意，利用数形结合的思想解答．
14．6
【分析】本题主要考查了特殊角三角函数的混合运算，牢记特殊角的三角函数值成为解题的关键．
先根据特殊角的三角函数值化简，然后再计算即可．
【详解】解：
．
故答案为6．
15．25.
【详解】试题解析：原式=3+1-3+24
=25．
考点：1.实数的运算；2.零指数幂；3.负整数指数幂；4.特殊角的三角函数值．
16．
【分析】先计算零指数幂、负指数幂、锐角三角函数值，再计算二次根式的乘法和加减法．
【详解】解：
故答案为：．
【点睛】本题主要考查了零指数幂、负指数幂、锐角三角函数值，熟练掌握零指数幂、负指数幂、锐角三角函数值的计算法则是解答本题的关键．
17．
【分析】设，则，根据正方形的性质结合翻折的性质得到，，根据等腰三角形的性质得到BG⊥AF，，利用三角形函数的定义即可求解．
【详解】∵，
∴设，则，
∵四边形是正方形，
∴，
根据翻折的性质知：，
设BC交AF于G，

∴BG⊥AF，且，
∴，
∵，
∴锐角，
故答案为：．
【点睛】本题考查了正方形的性质，翻折的性质，等腰三角形的判定和性质，特殊角的三角形函数值的应用，求得是解题的关键．
18．（1）；（2）；（3），
【分析】本题考查了特殊角的三角函数值，比例的性质，解一元二次方程；
（1）根据特殊角的三角函数值进行计算即可求解；
（2）设，，代入代数式，即可求解；
（3）根据公式法解一元二次方程，即可求解．
【详解】解：（1）原式；
（2）设，，
则；
（3）∵，，，
∴，
∴，
∴，；
19．见解析
【分析】本题考查特殊角度的三角函数，尺规作图，由为直角和可得，，先作线段的中点，再分别以、为圆心，长为半径画圆交点即为点．
【详解】如图，即为所求：
20．（1）；（2）
【分析】本题考查了特殊角的三角函数值计算和相似三角形的应用等知识．
（1）根据特殊角的三角函数值进行化简，再进行计算即可求解；
（2）先证明，得到，代入即可求解．
【详解】解：（1）
；
（2）∵和均为直角，
∴，
∴，
∴，
∵，，，
∴，
∴．
21．(1)
(2)
【分析】本题考查了特殊角度三角函数、勾股定理、直角三角形的知识；
（1）根据特殊角度三角函数的性质，推导得以及，从而完成求解；
（2）结合（1）的结论，根据勾股定理的性质计算得；根据特殊角度三角函数和含角直角三角形的性质计算得，即可得到答案．
【详解】（1）∵
∴
∴
∵，
∴．
∴
∴旗杆部分的长；
（2）∵，，，
∴
∵
∴
∵，
∴
∴钢丝的总长度．
22．（1）；（2），
【分析】此题考查了零指数幂、负整数指数幂和特殊角的三角函数值，解一元二次方程，解题的关键是熟练掌握以上运算法则．
（1）先化简二次根式，负整数指数幂，零指数幂，代入特殊角三角函数值，然后再计算；
（2）利用公式法解一元二次方程．
【详解】解：（1）
=
=；
（2）
，，
，
∴原方程有两个不相等的实数根，
∴，
∴，．
23．（1）见解析；（2）tan∠AED=．
【分析】（1）证明△CDE≌△CBE，根据全等三角形的性质得到ED＝EB，∠DEC＝∠BEC，根据平行线的性质、等腰三角形的判定定理得到DE＝DF，根据菱形的判定定理证明；
（2）根据矩形的性质得到∠BGD＝90°，DG＝AB＝5，AD＝BG，根据勾股定理求出GC，求出AD，根据勾股定理列方程求出AE，根据正切的定义计算，得到答案．
【详解】解：（1）证明：∵CE平分∠DCB，
∴∠DCE＝∠BCE，
在△CDE和△CBE中，
∴△CDE≌△CBE（SAS），
∴ED＝EB，∠DEC＝∠BEC，
∵DF//AB，
∴∠DFE＝∠BEC，
∴∠DFE＝∠DEC，
∴DE＝DF，
∴DF＝BE，又DF//AB，DE＝DF，
∴四边形DEBF为菱形；
（2）∵AD//BC，AB//DF，
∴四边形ABGD为平行四边形，
∵∠A＝90°，
∴四边形ABGD为矩形，
∴∠BGD＝90°，DG＝AB＝5，AD＝BG，
在Rt△DGC中，GC＝＝12，
∴AD＝BG＝BC﹣GC＝13﹣12＝1，
设AE＝x，则DE＝BE＝5﹣x，
在Rt△ADE中，DE2＝AE2+AD2，即(5﹣x)2＝x2+12，
解得，x＝，
∴tan∠AED＝＝．
【点睛】本题考查的是菱形的性质、全等三角形的判定和性质、锐角三角函数的定义，掌握菱形的判定定理、全等三角形的判定定理和性质定理是解题的关键．
24．(1)见解析
(2)
【分析】（1）根据三角形函数的定义和线段中点定义，得出，证明，得出结果即可；
（2）过E作于M，于N，证明，得出，证明，得出，根据，，得出即可．
【详解】（1）证明：，
，
∴，
为AB的中点，
，
，
，
，
，
，
，
∵，
∴，
∴，
，
．
（2）解：过E作于M，于N，

，
，
，
四边形内角和为，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
．
【点睛】本题主要考查了解直角三角形，三角函数的应用，三角形全等的判定和性质，三角形相似的判定和性质，解题的关键是作出辅助线，熟练掌握相似三角形和全等三角形的判定方法．
题号
1
2
3
4
5
6
7
8
9
10
答案
A
C
C
D
B
A
A
B
D
D
题号
11
12








答案
A
B