【备战2025年中考】一轮复习 初中数学 真题分项汇编 专题训练35 综合与实践探究类问题（原卷版+解析版）

这是一份【备战2025年中考】一轮复习 初中数学 真题分项汇编 专题训练35 综合与实践探究类问题（原卷版+解析版），文件包含备战2025年中考一轮复习初中数学真题分项汇编专题35综合与实践探究类问题原卷版doc、备战2025年中考一轮复习初中数学真题分项汇编专题35综合与实践探究类问题解析版doc等2份试卷配套教学资源，其中试卷共57页， 欢迎下载使用。
1. （2024黑龙江绥化）综合与实践
问题情境
在一次综合与实践课上，老师让同学们以两个全等的等腰直角三角形纸片为操作对象．
纸片和满足，．
下面是创新小组的探究过程．
操作发现
（1）如图1，取的中点，将两张纸片放置在同一平面内，使点与点重合．当旋转纸片交边于点、交边于点时，设，，请你探究出与的函数关系式，并写出解答过程．
问题解决
（2）如图2，在（1）的条件下连接，发现的周长是一个定值．请你写出这个定值，并说明理由．
拓展延伸
（3）如图3，当点在边上运动（不包括端点、），且始终保持．请你直接写出纸片的斜边与纸片的直角边所夹锐角的正切值______（结果保留根号）．

【答案】（1），见解析；（2）2，见解析；（3）或
【解析】【分析】（1）根据题意证明，得出关系式，进而求得，代入比例式，即可求解；
（2）方法一：勾股定理求得，将将（1）中代入得，进而根据三角形的周长公式，即可求解；
方法二：证明，，过作交于点，作交于点，作交于点．证明，，得出，得出，进而根据三角形的周长公式可得的周长．
方法三：过作交于点，作交于点，在上截取一点，使，连接．得出，，则，同方法二求得，进而即可求解；
（3）分两种情况讨论，于的夹角；①过点作于点，作的垂直平分线交于点，连接，在中，设，由勾股定理得，，进而根据正确的定义，即可求解；②过点作于点，作的垂直平分线交于点，连接，在中，设，同①即可求解．．
【详解】操作发现
解：（1）∵，且．
∴，
∴，
∴，
∴，
∴，
∴．
在中，，
∴，
∵是的中点，点与点重合，
∴，
∴，
∴．

问题解决
（2）方法一：
解：的周长定值为2．
理由如下：∵，，，
∴，，
在中，∴
．
将（1）中代入得：
∴．
∵，又∵，
∴，
∴．
∵的周长，
∴的周长．
方法二：
解：的周长定值为2．
理由如下：∵和等腰直角三角形，
∴，
∵，
∴，
在中，，
∴，
∴，
∴，
∴，，，
∵O为AB的中点，
∴，
∴，
又∵，
∴，
，，
∴过作交于点，作交于点，作交于点．
∴．
又∵，，
∴，，
∴，，
∴．
∵的周长．
又∵，，，
∴，
∴，
∵，，
∴，
∵是的中点，
点是的中点，同理点是的中点．
∴，
∴的周长．

方法三：
解：的周长定值为2．
理由如下：过作交于点，作交于点，在上截取一点，使，连接．
∵是等腰直角三角形，为的中点，
∴平分，
∴，
∴，
∴，．
∵，，
∴，，
∴，
∴，
∵，
∴，
∴，
∴周长．
又∵，，，
∴，
∴．
∵，，
∴．
∵是的中点，点是的中点，同理点是的中点．
∴，
∴的周长．

拓展延伸
（3）或
①解：∵，，
∴，
过点作于点，作的垂直平分线交于点，连接，
∴，
∵，
∴，
∵，
∴，
∴，
在中，设，
∴，由勾股定理得，
，
∴，
∴在中，．

②解：∵，，
∴，
过点作于点，作的垂直平分线交于点，连接．
∵，
∴，
∴，
在中，设，
∴，由勾股定理得，，
∴，
∴在中，．
∴或．

【点睛】本题考查了相似三角形的性质与判定，全等三角形的性质与判定，解直角三角形，旋转的性质，函数解析式，熟练掌握相似三角形的性质与判定，解直角三角形是解题的关键．
2. （2024福建省）在手工制作课上，老师提供了如图1所示的矩形卡纸，要求大家利用它制作一个底面为正方形的礼品盒．小明按照图2的方式裁剪（其中），恰好得到纸盒的展开图，并利用该展开图折成一个礼品盒，如图3所示．
图1 图2 图3
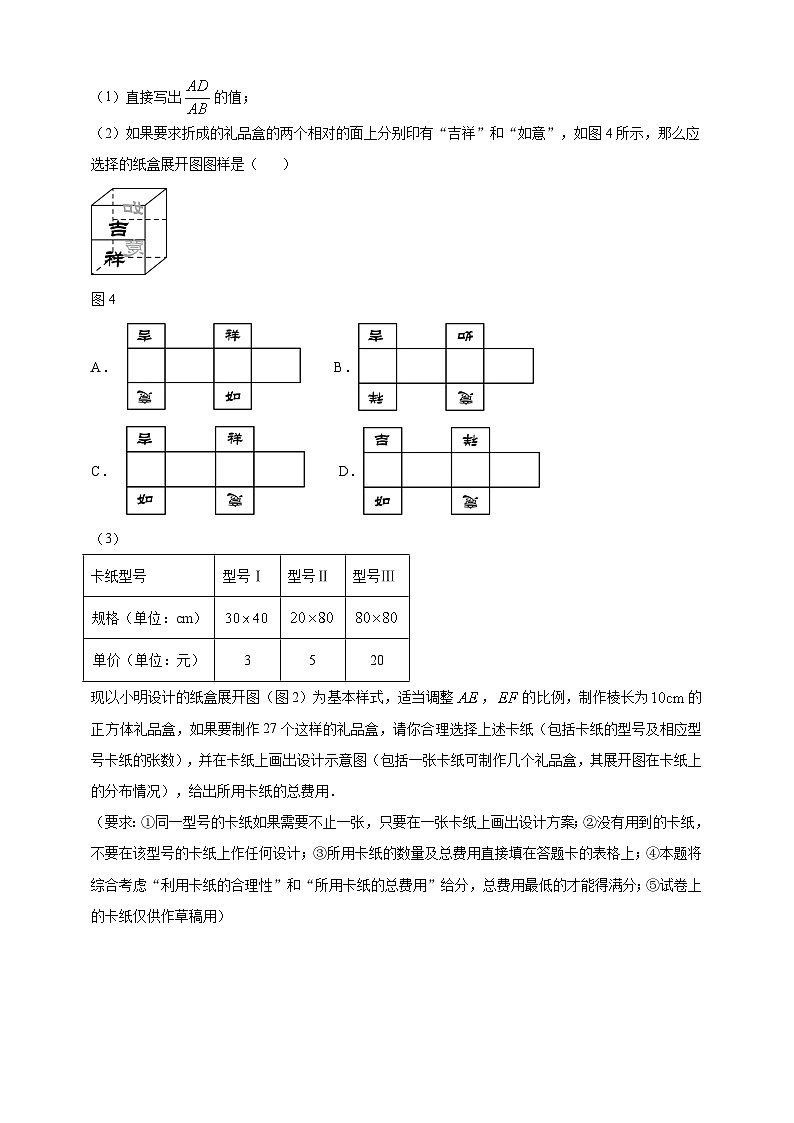
（1）直接写出的值；
（2）如果要求折成的礼品盒的两个相对的面上分别印有“吉祥”和“如意”，如图4所示，那么应选择的纸盒展开图图样是（ ）
图4
A． B．
C． D．
（3）
现以小明设计的纸盒展开图（图2）为基本样式，适当调整，的比例，制作棱长为的正方体礼品盒，如果要制作27个这样的礼品盒，请你合理选择上述卡纸（包括卡纸的型号及相应型号卡纸的张数），并在卡纸上画出设计示意图（包括一张卡纸可制作几个礼品盒，其展开图在卡纸上的分布情况），给出所用卡纸的总费用．
（要求：①同一型号的卡纸如果需要不止一张，只要在一张卡纸上画出设计方案；②没有用到的卡纸，不要在该型号的卡纸上作任何设计；③所用卡纸的数量及总费用直接填在答题卡的表格上；④本题将综合考虑“利用卡纸的合理性”和“所用卡纸的总费用”给分，总费用最低的才能得满分；⑤试卷上的卡纸仅供作草稿用）
【答案】（1）2； （2）C； （3）见解析．
【解析】本题考查了几何体的展开与折叠，空间观念、推理能力、模型观念、创新意识等知识，掌握相关知识是解题的关键．
（1）由折叠和题意可知，，，四边形是正方形，得到，即，即可求解；
（2）根据几何体的展开图即可求解；
（3）由题意可得，每张型号卡纸可制作10个正方体，每张型号卡纸可制作2个正方体，每张型号卡纸可制作1个正方体，即可求解．
【小问1详解】
解：如图：
上述图形折叠后变成：
由折叠和题意可知，，，
∵四边形正方形，
∴，即，
∴，即，
∵，
∴，
∴的值为：．
【小问2详解】
解：根据几何体的展开图可知，“吉”和“如”在对应面上，“祥”和“意”在对应面上，而对应面上的字中间相隔一个几何图形，且字体相反，
∴C选项符合题意，
故选：C．
【小问3详解】
解：
根据（1）和题意可得：卡纸每格的边长为，则要制作一个边长为的正方体的展开图形为：
∴型号卡纸，每张卡纸可制作10个正方体，如图：
型号卡纸，每张这样的卡纸可制作2个正方体，如图：
型号卡纸，每张这样的卡纸可制作1个正方体，如图：
∴可选择型号卡纸2张，型号卡纸3张，型号卡纸1张，则
（个），
∴所用卡纸总费用为：
（元）．
3. （2024甘肃威武）【模型建立】
（1）如图1，已知和，，，，．用等式写出线段，，的数量关系，并说明理由．
【模型应用】
（2）如图2，在正方形中，点E，F分别在对角线和边上，，．用等式写出线段，，的数量关系，并说明理由．
【模型迁移】
（3）如图3，在正方形中，点E在对角线上，点F在边的延长线上，，．用等式写出线段，，的数量关系，并说明理由．
【答案】（1），理由见详解，（2），理由见详解，（3），理由见详解
【解析】
【分析】（1）直接证明，即可证明；
（2）过E点作于点M，过E点作于点N，先证明，可得，结合等腰直角三角形的性质可得：， ，即有，，进而可得，即可证；
（3）过A点作于点H，过F点作，交的延长线于点G，先证明，再结合等腰直角三角形的性质，即可证明．
【详解】（1），理由如下：
∵，，，
∴，
∴，
∴，
∵，
∴，
∴，，
∴，
∴；
（2），理由如下：
过E点作于点M，过E点作于点N，如图，
∵四边形是正方形，是正方形的对角线，
∴，平分，，
∴，
即，
∵，，
∴，
∵，
∴，
∴，
∵，，，，
∴四边形是正方形，
∴是正方形对角线，，
∴， ，
∴，，
∴，即，
∵，
∴，
即有；
（3），理由如下，
过A点作于点H，过F点作，交的延长线于点G，如图，
∵，，，
∴，
∴，
∴，
又∵，
∴，
∴，
∵在正方形中，，
∴，
∴，
∴是等腰直角三角形，
∴，
∴，
∵，，
∴是等腰直角三角形，
∴，
∴，
∴，
∵，
∴，
∴．
【点睛】本题主要考查了正方形的性质，等腰直角三角形的性质，全等三角形的判定与性质，角平分线的性质等知识，题目难度中等，作出合理的辅助线，灵活证明三角形的全等，并准确表示出各个边之间的数量关系，是解答本题的关键．
4. （2024广西）综合与实践
在综合与实践课上，数学兴趣小组通过洗一套夏季校服，探索清洗衣物的节约用水策略．
【洗衣过程】
步骤一：将校服放进清水中，加入洗衣液，充分浸泡揉搓后拧干；
步骤二：将拧干后的校服放进清水中，充分漂洗后拧干．重复操作步骤二，直至校服上残留洗衣液浓度达到洗衣目标．
假设第一次漂洗前校服上残留洗衣液浓度为，每次拧干后校服上都残留水．
浓度关系式：．其中、分别为单次漂洗前、后校服上残留洗衣液浓度；w为单次漂洗所加清水量（单位：）
【洗衣目标】经过漂洗使校服上残留洗衣液浓度不高于
【动手操作】请按要求完成下列任务：
（1）如果只经过一次漂洗，使校服上残留洗衣液浓度降为，需要多少清水？
（2）如果把清水均分，进行两次漂洗，是否能达到洗衣目标？
（3）比较（1）和（2）的漂洗结果，从洗衣用水策略方面，说说你的想法．
【答案】（1）只经过一次漂洗，使校服上残留洗衣液浓度降为，需要清水．
（2）进行两次漂洗，能达到洗衣目标；
（3）两次漂洗的方法值得推广学习
【解析】
【分析】本题考查的是分式方程的实际应用，求解代数式的值，理解题意是关键；
（1）把，代入， 再解方程即可；
（2）分别计算两次漂洗后的残留洗衣液浓度，即可得到答案；
（3）根据（1）（2）的结果得出结论即可．
【小问1详解】
解：把，代入
得，
解得．经检验符合题意；
∴只经过一次漂洗，使校服上残留洗衣液浓度降为，需要清水．
【小问2详解】
解：第一次漂洗：
把，代入，
∴，
第二次漂洗：
把，代入，
∴，
而，
∴进行两次漂洗，能达到洗衣目标；
【小问3详解】
解：由（1）（2）的计算结果发现：经过两次漂洗既能达到洗衣目标，还能大幅度节约用水，
∴从洗衣用水策略方面来讲，采用两次漂洗的方法值得推广学习．
5. （2024贵州省）综合与探究：如图，，点P在的平分线上，于点A．
（1）【操作判断】
如图①，过点P作于点C，根据题意在图①中画出，图中的度数为______度；
（2）【问题探究】
如图②，点M在线段上，连接，过点P作交射线于点N，求证：；
（3）【拓展延伸】
点M在射线上，连接，过点P作交射线于点N，射线与射线相交于点F，若，求的值．
【答案】（1）画图见解析，90 （2）见解析 （3）或
【解析】【分析】（1）依题意画出图形即可，证明四边形是矩形，即可求解；
（2）过P作于C，证明矩形是正方形，得出，利用证明，得出，然后利用线段的和差关系以及等量代换即可得证；
（3）分M在线段，线段的延长线讨论，利用相似三角形的判定与性质求解即可；
【小问1详解】
解：如图，即为所求，
∵，，，
∴四边形是矩形，
∴，
故答案为：90；
【小问2详解】
证明：过P作于C，
由（1）知：四边形是矩形，
∵点P在的平分线上，，，
∴，
∴矩形是正方形，
∴，，
∵，
∴，
又，，
∴，
∴，
∴
；
【小问3详解】
解：①当M在线段上时，如图，延长、相交于点G，
由（2）知，
设，则，，
∴，
∵，，
∴，
∴，
∵，，
∴，
∴，
∴，
∴，
∴；
②当M在的延长线上时，如图，过P作于C，并延长交于G
由（2）知：四边形是正方形，
∴，，，
∵，
∴，
又，，
∴，
∴，
∴
，
∵
∴，，
∵，
∴，
∴，即，
∴，
∵，
∴，
∴，
∴，
∴；
综上，的值为或．
【点睛】本题考查了矩形的判定与性质，正方形的判定与性质，角平分线的性质，全等三角形的判断与性质，相似三角形的判断与性质等知识，明确题意，添加合适辅助线，构造全等三角形、相似三角形，合理分类讨论是解题的关键．
6. （2024河北省）情境 图1是由正方形纸片去掉一个以中心O为顶点的等腰直角三角形后得到的．
该纸片通过裁剪，可拼接为图2所示的钻石型五边形，数据如图所示．
（说明：纸片不折叠，拼接不重叠无缝隙无剩余）
操作 嘉嘉将图1所示的纸片通过裁剪，拼成了钻石型五边形．
如图3，嘉嘉沿虚线，裁剪，将该纸片剪成①，②，③三块，再按照图4所示进行拼接．根据嘉嘉的剪拼过程，解答问题：
（1）直接写出线段的长；
（2）直接写出图3中所有与线段相等的线段，并计算的长．
探究淇淇说：将图1所示纸片沿直线裁剪，剪成两块，就可以拼成钻石型五边形．
请你按照淇淇的说法设计一种方案：在图5所示纸片的边上找一点P（可以借助刻度尺或圆规），画出裁剪线（线段）的位置，并直接写出的长．
【答案】（1）；（2），；的长为或．
【解析】【分析】本题考查的是正方形的性质，等腰直角三角形的判定与性质，勾股定理的应用，二次根式的混合运算，本题要求学生的操作能力要好，想象能力强，有一定的难度．
（1）如图，过作于，结合题意可得：四边形为矩形，可得，由拼接可得：，可得，，为等腰直角三角形，为等腰直角三角形，设，则，再进一步解答即可；
（2）由为等腰直角三角形，；求解，再分别求解；可得答案，如图，以为圆心，为半径画弧交于，交于，则直线为分割线，或以圆心，为半径画弧，交于，交于，则直线为分割线，再进一步求解的长即可．
【详解】解：如图，过作于，
结合题意可得：四边形为矩形，
∴，
由拼接可得：，
由正方形的性质可得：，
∴，，为等腰直角三角形，
∴为等腰直角三角形，
设，
∴，
∴，，
∵正方形的边长为，
∴对角线的长，
∴，
∴，
解得：，
∴；
（2）∵为等腰直角三角形，；
∴，
∴，
∵，
，
∴；
如图，以为圆心，为半径画弧交于，交于，则直线为分割线，
此时，，符合要求，
或以圆心，为半径画弧，交于，交于，则直线为分割线，
此时，，
∴，
综上：的长为或．
7. （2024河南省）综合与实践
在学习特殊四边形的过程中，我们积累了一定的研究经验，请运用已有经验，对“邻等对补四边形”进行研究
定义：至少有一组邻边相等且对角互补的四边形叫做邻等对补四边形．

（1）操作判断
用分别含有和角的直角三角形纸板拼出如图1所示的4个四边形，其中是邻等对补四边形的有________（填序号）．
（2）性质探究
根据定义可得出邻等对补四边形的边、角的性质．下面研究与对角线相关的性质．
如图2，四边形是邻等对补四边形，，是它的一条对角线．
①写出图中相等的角，并说明理由；
②若，，，求的长（用含m，n，的式子表示）．
（3）拓展应用
如图3，在中，，，，分别在边，上取点M，N，使四边形是邻等对补四边形．当该邻等对补四边形仅有一组邻边相等时，请直接写出的长．
【答案】（1）②④ （2）①．理由见解析；②
（3）或
【解析】【分析】（1）根据邻等对补四边形的定义判断即可；
（2）①延长至点E，使，连接，根据邻等对补四边形定义、补角的性质可得出，证明，得出，，根据等边对等角得出，即可得出结论；
②过A作于F，根据三线合一性质可求出，由①可得，在中，根据余弦的定义求解即可；
（3）分，，，四种情况讨论即可．
【小问1详解】
解：观察图知，图①和图③中不存在对角互补，图2和图4中存在对角互补且邻边相等，
故图②和图④中四边形是邻等对补四边形，
故答案为：②④；
【小问2详解】
解：①，理由：
延长至点E，使，连接，
∵四边形是邻等对补四边形，
∴，
∵，
∴，
∵，
∴，
∴，，
∴，
∴；
②过A作于F，
∵，
∴，
∵，
∴，
在中，，
∴；
【小问3详解】
解：∵，，，
∴，
∵四边形是邻等对补四边形，
∴，
∴，
当时，如图，连接，过N作于H，
∴，
在中，
在中，
∴，
解得，
∴，
∵，，
∴，
∴，即，
∴，，
∴，
∴；
当时，如图，连接，
∵，
∴，
∴，故不符合题意，舍去；
当时，连接，过N作于H，
∵，，
∴，
∴，即，
解得，
∵，，
∴，
∴，即，
∴，，
∴，
∴；
当时，如图，连接，
∵，
∴，
∴，故不符合题意，舍去；
综上，的长为或．
【点睛】本题考查了相似三角形判定与性质，等腰三角形的性质，全等三角形的判定与性质，解直角三角形，勾股定理等知识，明确题意，理解新定义，添加合适辅助线，构造全等三角形、相似三角形是解题的关键．
8. （2024黑龙江齐齐哈尔）综合与实践：如图1，这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”，受这幅图的启发，数学兴趣小组建立了“一线三直角模型”．如图2，在中，，将线段绕点顺时针旋转得到线段，作交的延长线于点．

（1）【观察感知】如图2，通过观察，线段与的数量关系是______；
（2）【问题解决】如图3，连接并延长交的延长线于点，若，，求的面积；
（3）【类比迁移】在(2)的条件下，连接交于点，则______；
（4）【拓展延伸】在(2)的条件下，在直线上找点，使，请直接写出线段的长度．
【答案】（1） （2）10 （3） （4）或
【解析】【分析】（1）根据旋转的性质可得，，进而证明，即可求解；
（2）根据（1）的方法证明，进而证明，求得，则，然后根据三角形的面积公式，即可求解．
（3）过点作于点，证明得出，证明，设，则，代入比例式，得出，进而即可求解；
（4）当在点的左侧时，过点作于点，当在点的右侧时，过点作交的延长线于点，分别解直角三角形，即可求解．
【小问1详解】
解：∵将线段绕点顺时针旋转得到线段，作交的延长线于点．

，
，
，
，
，
又且
，
；
【小问2详解】
解：，
，
，
，
，
又且，
，
，
，
，
，

，
，
，
，
；
【小问3详解】
解：如图所示，过点作于点，

∵，
∴
∴，
即，即，
又∵
∴
∴，
设，则，
解得：
∴；
【小问4详解】
解：如图所示，当在点的左侧时，过点作于点

∵
∴，设，则，
又∵，
∴，
∴
∴
∴
∴，
解得：
在中，
∴
∴
如图所示，当在点的右侧时，过点作交的延长线于点，

∵
∴
∵
∴
设，则，，
∵，
∴
解得：
∴
∴
综上所述，或．
【点睛】本题考查了全等三角形的性质与判定，相似三角形的性质与判定，解直角三角形，旋转的性质，熟练掌握以上知识是解题的关键．
9. （2024黑龙江绥化）综合与探究
如图，在平面直角坐标系中，已知抛物线与直线相交于，两点，其中点，．
（1）求该抛物线的函数解析式．
（2）过点作轴交抛物线于点，连接，在抛物线上是否存在点使．若存在，请求出满足条件的所有点的坐标；若不存在，请说明理由．（提示：依题意补全图形，并解答）
（3）将该抛物线向左平移个单位长度得到，平移后的抛物线与原抛物线相交于点，点为原抛物线对称轴上的一点，是平面直角坐标系内的一点，当以点、、、为顶点的四边形是菱形时，请直接写出点F的坐标．
【答案】（1）
（2）存在，点坐标为，，补图见解析
（3）、、、
【解析】
【分析】（1）待定系数法求解析式即可求解；
（2）根据平行线的性质可得，求得，进而分别求得，，根据可得，设直线交轴于点，则，．进而可得，的解析式为，，连接交抛物线于，连接交抛物线于，进而联立抛物线与直线解析式，解方程，即可求解．
（3）①以为对角线，如图作的垂直平分线交于点交直线于，设，根据两点距离公式可得，根据中点坐标公式可得，②以为边，如图以为圆心，为半径画圆交直线于点，；连接，，根据勾股定理求得，进而得出，，根据平移的性质得出，，③以为边，如图以点为圆心，长为半径画圆交直线于点和，连接，，则，过点作于点，则，在和中，由勾股定理得，则、，根据，可得，过点作，过作，和相交于点，的中点．根据中点坐标公式可得；
【小问1详解】
解：∵把点，代入得
，
解得，
∴．
【小问2详解】
存在．
理由：∵轴且，
∴，
∴（舍去），，
∴．
过点作于点，
在中，
∵，
∴，
∵，
∴．
设直线交轴于点，
，，
∴，．
连接交抛物线于，连接交抛物线于，
∴，的解析式为，，
∴，解得，
或，解得．
∴把，代入得，，
∴，．
综上所述，满足条件的点坐标为，．
【小问3详解】
、、、．
方法一：
①以为对角线，如图作垂直平分线交于点交直线于
∵，，
∴．
设，
∵，
∴，
∴，
∴，
∵是的中点，
．
②以为边
如图以为圆心，为半径画圆交直线于点，；连接，，
过点作，过点作，和相交于点，同理可得
，，
，
．
过点作直线于点，则；
在和中，由勾股定理得，
，
，．
点是由点向右平移个单位长度，再向上平移个单位长度得到的，
，，
③以为边
如图以点为圆心，长为半径画圆交直线于点和，
连接，，则，
过点作于点，则，在和中，由勾股定理得，
，
、，
，
，
、、三点共线，
过点作，过作，
和相交于点，
∵、，
的中点．
，点为的中点，
．
综上所述：、、、．
10. （2024吉林省）综合与实践
某班同学分三个小组进行“板凳中的数学”的项目式学习研究，第一小组负责调查板凳的历史及结构特点；第二小组负责研究板凳中蕴含的数学知识：第三小组负责汇报和交流，下面是第三小组汇报的部分内容，请你阅读相关信息，并解答“建立模型”中的问题．
【背景调查】
图①中的板凳又叫“四脚八叉凳”，是中国传统家具，其榫卯结构体现了古人含蓄内敛的审美观．榫眼的设计很有讲究，木工一般用铅笔画出凳面的对称轴，以对称轴为基准向两边各取相同的长度，确定榫眼的位置，如图②所示．板凳的结构设计体现了数学的对称美．
【收集数据】
小组收集了一些板凳并进行了测量．设以对称轴为基准向两边各取相同的长度为，凳面的宽度为，记录如下：
【分析数据】
如图③，小组根据表中x，y的数值，在平面直角坐标系中描出了各点．
【建立模型】
请你帮助小组解决下列问题：
（1）观察上述各点的分布规律，它们是否在同一条直线上？如果在同一条直线上，求出这条直线所对应的函数解析式；如果不在同一条直线上，说明理由．
（2）当凳面宽度为时，以对称轴为基准向两边各取相同的长度是多少？
【答案】（1）在同一条直线上，函数解析式为： （2）
【解析】【分析】本题考查了一次函数的实际应用，待定系数法求函数解析式，已知函数值求自变量，熟练掌握知识点，正确理解题意是解题的关键．
（1）用待定系数法求解即可；
（2）将代入函数解析式，解方程即可．
【小问1详解】
解：设函数解析式为：，
∵当，，
∴，
解得：，
∴函数解析式为：，
经检验其余点均在直线上，
∴函数解析式为，这些点在同一条直线上；
【小问2详解】
解：把代入得：
，
解得：，
∴当凳面宽度为时，以对称轴为基准向两边各取相同的长度为．
11. （2024江苏盐城）请根据以下素材，完成探究任务．
【答案】任务1：；任务2：；任务3：安排17名工人加工“雅”服装，17名工人加工“风”服装，34名工人加工“正”服装，即可获得最大利润
【解析】【分析】题目主要考查一次函数及二次函数的应用，理解题意，根据二次函数的性质求解是解题关键．
任务1：根据题意安排x名工人加工“雅”服装，y名工人加工“风”服装，得出加工“正”服装的有人，然后利用“正”服装总件数和“风”服装相等，得出关系式即可得出结果；
任务2：根据题意得：“雅”服装每天获利为：，然后将2种服装的获利求和即可得出结果；
任务3：根据任务2结果化为顶点式，然后结合题意，求解即可．
【详解】解：任务1：根据题意安排70名工人加工一批夏季服装，
∵安排x名工人加工“雅”服装，y名工人加工“风”服装，
∴加工“正”服装的有人，
∵“正”服装总件数和“风”服装相等，
∴，
整理得：；
任务2：根据题意得：“雅”服装每天获利为：，
∴，
整理得：
∴
任务3：由任务2得，
∴当时，获得最大利润，
，
∴，
∵开口向下，
∴取或，
当时，，不符合题意；
当时，，符合题意；
∴，
综上：安排17名工人加工“雅”服装，17名工人加工“风”服装，34名工人加工“正”服装，即可获得最大利润．
12. （2024江苏盐城）发现问题
小明买菠萝时发现，通常情况下，销售员都是先削去菠萝的皮，再斜着铲去菠萝的籽．
提出问题
销售员斜着铲去菠萝的籽，除了方便操作，是否还蕴含着什么数学道理呢？
分析问题
某菠萝可以近似看成圆柱体，若忽略籽的体积和铲去果肉的厚度与宽度，那么籽在侧面展开图上可以看成点，每个点表示不同的籽．该菠萝的籽在侧面展开图上呈交错规律排列，每行有n个籽，每列有k个籽，行上相邻两籽、列上相邻两籽的间距都为d（n，k均为正整数，，），如图1所示．
小明设计了如下三种铲籽方案．
方案1：图2是横向铲籽示意图，每行铲的路径长为________，共铲________行，则铲除全部籽的路径总长为________；
方案2：图3是纵向铲籽示意图，则铲除全部籽的路径总长为________；
方案3：图4是销售员斜着铲籽示意图，写出该方案铲除全部籽的路径总长．
解决问题
在三个方案中，哪种方案铲籽路径总长最短？请写出比较过程，并对销售员的操作方法进行评价．
【答案】分析问题：方案1：；；；方案2：；方案3：；解决问题：方案3路径最短，理由见解析
【解析】【分析】分析问题：方案1：根据题意列出代数式即可求解；方案2：根据题意列出代数式即可求解；方案3：根据图得出斜着铲每两个点之间的距离为，根据题意得一共有列，行，斜着铲相当于有n条线段长，同时有个，即可得出总路径长；
解决问题：利用作差法比较三种方案即可．
题目主要考查列代数式，整式的加减运算，二次根式的应用，理解题意是解题关键．
【详解】解：方案1：根据题意每行有n个籽，行上相邻两籽的间距为d，
∴每行铲的路径长为，
∵每列有k个籽，呈交错规律排列，
∴相当于有行，
∴铲除全部籽的路径总长为，
故答案为：；；；
方案2：根据题意每列有k个籽，列上相邻两籽的间距为d，
∴每列铲路径长为，
∵每行有n个籽，呈交错规律排列，，
∴相当于有列，
∴铲除全部籽的路径总长为，
故答案为：；
方案3：由图得斜着铲每两个点之间的距离为，
根据题意得一共有列，行，
斜着铲相当于有n条线段长，同时有个，
∴铲除全部籽的路径总长为：；
解决问题
由上得：，
∴方案1的路径总长大于方案2的路径总长；
，
∵，
当时，
，
，
∴方案3铲籽路径总长最短，销售员的操作方法是选择最短的路径，减少对菠萝的损耗．
13. （2024内蒙古赤峰）数学课上，老师给出以下条件，请同学们经过小组讨论，提出探究问题．如图1，在中，，点D是上的一个动点，过点D作于点E，延长交延长线于点F．
请你解决下面各组提出的问题：
（1）求证：；
（2）探究与的关系；
某小组探究发现，当时，；当时，．
请你继续探究：
①当时，直接写出的值；
②当时，猜想的值（用含m，n的式子表示），并证明；
（3）拓展应用：在图1中，过点F作，垂足为点P，连接，得到图2，当点D运动到使时，若，直接写出的值（用含m，n的式子表示）．
【答案】（1）见解析 （2）①②，证明见解析
（3）
【解析】【分析】（1）等边对等角，得到，等角的余角的相等，结合对顶角相等，得到，即可得出结论；
（2）①根据给定的信息，得到是的2倍，即可得出结果；
②猜想，作于点，证明，得到，三线合一得到，即可得出结论；
（3）过点作，角平分线的性质，得到，推出，等角的余角相等，得到，进而得到，得到，根据，即可得出结果．
【小问1详解】
证明：∵，
∴，
∵，
∴，
∴，，且，
∴，
∴；
【小问2详解】
解：①当时，；当时，，
∴总结规律得：是的2倍，
∴当时，；
②当时，猜想，
证明：作于点，
∵，
∴，
∴，
∵，
∴，
由（1）知，又，
∴，即，
∴；
【小问3详解】
，理由如下：
过点作，
∵，，
∴，
由（2）知，当时，，
∴，
∴，
∵，
∴，
∵，
∴，
∵，
∴，
∴，
∴，
∴，
∴，
∴，
∴，
由（1）知，
∴．
【点睛】本题考查等腰三角形的判定和性质，角平分线的性质，相似三角形的判定和性质，解直角三角形等知识点，熟练掌握相关知识点，添加辅助线构造特殊图形和相似三角形，是解题的关键．
卡纸型号
型号Ⅰ
型号Ⅱ
型号Ⅲ
规格（单位：cm）
单价（单位：元）
3
5
20
卡纸型号
型号
型号
型号
需卡纸的数量（单位：张）
1
3
2
所用卡纸总费用（单位：元）
58
以对称轴为基准向两边各取相同的长度
16.5
198
23.1
26.4
29.7
凳面的宽度
115.5
132
148.5
165
181.5
制定加工方案
生产背景
背景1
◆某民族服装厂安排70名工人加工一批夏季服装，有“风”“雅”“正”三种样式．
◆因工艺需要，每位工人每天可加工且只能加工“风”服装2件，或“雅”服装1件，或“正”服装1件．
◆要求全厂每天加工“雅”服装至少10件，“正”服装总件数和“风”服装相等.
背景2
每天加工的服装都能销售出去，扣除各种成本，服装厂的获利情况为：
①“风”服装：24元/件；
②“正”服装：48元/件；
③“雅”服装：当每天加工10件时，每件获利100元；如果每天多加工1件，那么平均每件获利将减少2元．
信息整理
现安排x名工人加工“雅”服装，y名工人加工“风”服装，列表如下：
服装种类
加工人数（人）
每人每天加工量（件）
平均每件获利（元）
风
y
2
24
雅
x
1
正
1
48
探究任务
任务1
探寻变量关系
求x、y之间的数量关系．
任务2
建立数学模型
设该工厂每天的总利润为w元，求w关于x的函数表达式．
任务3
拟定加工方案
制定使每天总利润最大的加工方案．