湘教版（2024）七年级下册（2024）4.3 平行线的性质精品课件ppt

这是一份湘教版（2024）七年级下册（2024）4.3 平行线的性质精品课件ppt，文件包含43平行线的性质pptx、43平行线的性质doc等2份课件配套教学资源，其中PPT共23页， 欢迎下载使用。
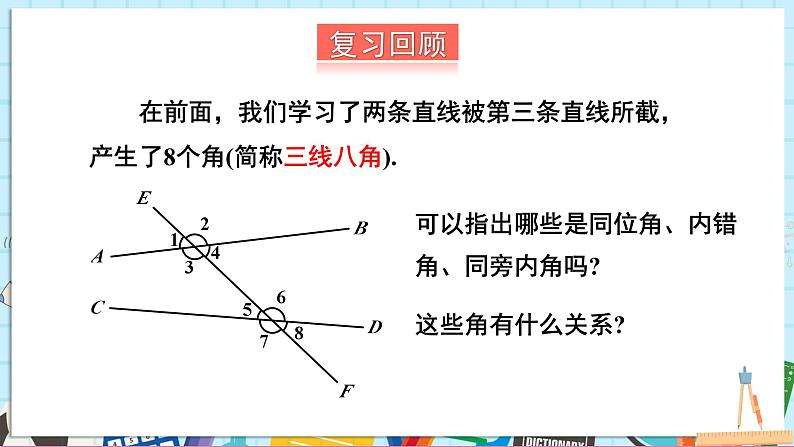
在前面，我们学习了两条直线被第三条直线所截，产生了8个角(简称三线八角).
可以指出哪些是同位角、内错角、同旁内角吗?
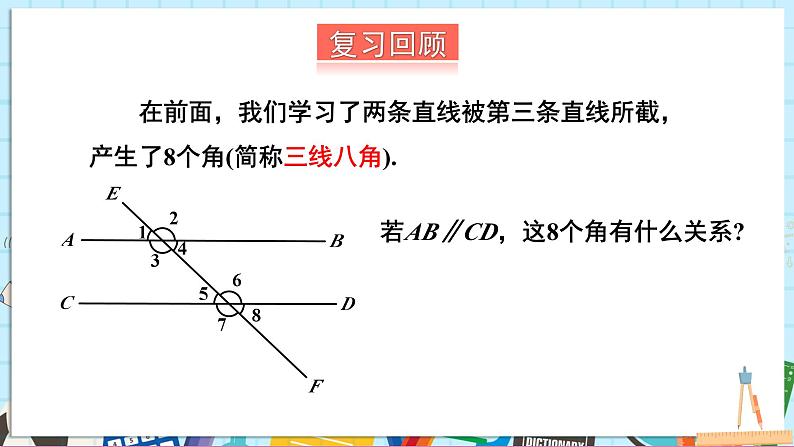
若AB∥CD，这8个角有什么关系?
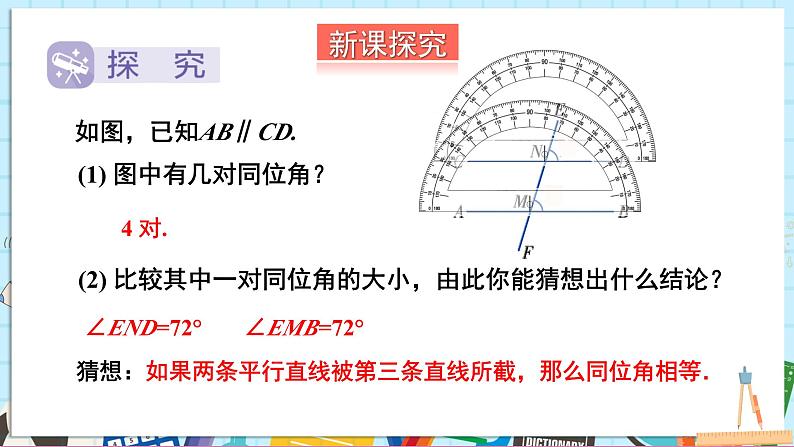
如图，已知AB∥CD.
(1) 图中有几对同位角？
(2) 比较其中一对同位角的大小，由此你能猜想出什么结论？
猜想：如果两条平行直线被第三条直线所截，那么同位角相等．
如图，设 AB//CD，直线EF 与 直线AB，CD 分别相交于 M，N 两点．则∠EMB和∠END是一对同位角，分别记为∠α和∠β.
移动后，点M的对应点是点N，射线ME的像是射线NE，直线AB的像是直线CD，射线MB的像是射线ND，∠α的像是∠β. 根据平移的知识得，∠α =∠β
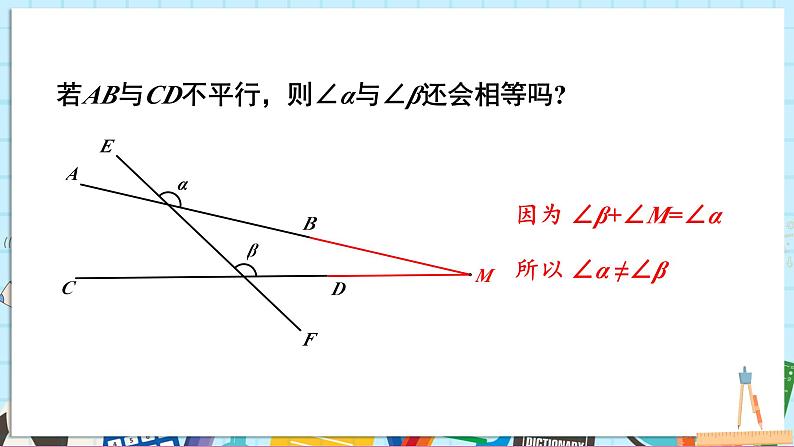
若AB与CD不平行，则∠α与∠β还会相等吗?
因为 ∠β+∠M=∠α
简单说成：两直线平行，同位角相等.
一般地，平行线具有如下性质：
性质1 两条平行直线被第三条直线所截，同位角相等.
两条平行直线被第三条直线所截，一对内错角的大小有什么关系？
如图，已知AB∥CD，那么∠1与∠2相等吗?
因为 AB∥CD，所以∠1 =∠4（两直线平行，同位角相等）.又因为∠2 ＝∠4 （对顶角相等），所以∠1 ＝∠2 （等量代换）.
简单说成：两直线平行，内错角相等.
性质2 两条平行直线被第三条直线所截，内错角相等.
因为 AB∥CD，所以∠1 =∠4（两直线平行，同位角相等）.又因为∠3 +∠4 = 180°，所以∠1 +∠3 = 180° （等量代换）.
如图，已知AB∥CD，那么∠1与∠3 有什么关系?为什么?
两条平行直线被第三条直线所截，一对同旁内角有什么关系？为什么？
简单说成：两直线平行，同旁内角互补.
性质3 两条平行直线被第三条直线所截，同旁内角互补.
解：因为 AB∥CD，所以∠1 ＝∠2 ＝ 100°(两直线平行，同位角相等)又因为∠2 +∠3 = 180°，所以∠3 = 180° -∠2 = 180° - 100° = 80°.
在例 1 中，分别用平行线的性质 2 和性质 3 求出∠3 的度数.
解：因为 AB∥CD，所以∠1 ＝∠4 ＝ 100°(两直线平行，内错角相等)又因为∠3 +∠4 = 180°，所以∠3 = 180° -∠4 = 180° - 100° = 80°.
解：因为 AB∥CD，所以∠5 ＝180°-∠1 ＝ 80°(两直线平行，同旁内角互补)又因为∠3 =∠5 （对顶角相等）所以∠3 = 80°（等量代换）.
解 ：因为 AD∥BC，所以∠A +∠B = 180°∠D +∠C = 180° （两直线平行， 同旁内角互补）.又因为∠B =∠D （已知），所以∠A ＝∠C.
1.填空:(1)如图，因为AB∥CD，所以∠1=______，理由是___________________________;(2)如图，因为AB∥CD，所以∠D=______，理由是___________________________.
两直线平行，同位角相等
两直线平行，内错角相等
[选自教材P105 练习]
2. 如图，AB∥CD∥EF， BC∥ED， ∠B ＝ 70°，求∠C，∠D 和 ∠E 的度数．
解： 因为AB∥CD， ∠B ＝ 70°，所以 ∠C ＝∠B ＝ 70°(两直线平行，内错角相等)又因为 BC∥ED， 所以 ∠C + ∠D ＝180°(两直线平行，同旁内角互补)所以 ∠D ＝180°- 70°=110°因为 CD∥EF， 所以 ∠E ＝∠D ＝ 110°(两直线平行，内错角相等)
3. 如图，直线 AB，CD 被直线 EF 所截，AB∥CD，∠1 ＝ 105°. 求∠2，∠3，∠4 的度数.
解 ：因为 AB∥CD， ∠1 = 105°，所以∠2 =∠1 = 105°(两直线平行， 内错角相等) 所以∠3 =180°-∠1=75°(两直线平行，同旁内角互补)所以∠4 =∠1 = 105°(两直线平行， 同位角相等)
4. 如图，已知AB∥CD，AP 平分∠BAC，CP 平分∠ACD，∠1+∠2=90°吗？
解：因为 AB∥CD，所以∠BAC+ ∠ACD = 180°(两直线平行，同旁内角互补) 又因为AP平分∠BAC，CP平分∠ACD，
1.如图，一把长方形直尺沿直线断开并错位，点 E、D、B、F在同一条直线上，若∠ADE=125°, 则∠DBC的度数为 ( )A.55° B.65° C.75° D.125°
2. 如图，AB∥CD，BF∥CE，则∠B 与∠C有什么关系？请说明理由.
解：因为AB∥CD，所以∠B =∠1 (两直线平行， 内错角相等) 因为 BF∥CE，所以 ∠C =∠2 (两直线平行， 内错角相等) 因为∠1 +∠2 = 180°，所以∠B +∠C = 180°，即∠B 与∠C 互补.
两直线平行，同位角相等.
两直线平行，内错角相等.
两直线平行，同旁内角互补.