湘教版（2024）七年级下册（2024）4.5 垂线试讲课ppt课件

这是一份湘教版（2024）七年级下册（2024）4.5 垂线试讲课ppt课件，文件包含452垂线段与点到直线的距离pptx、452垂线段与点到直线的距离doc等2份课件配套教学资源，其中PPT共24页， 欢迎下载使用。
在灌溉时，要把河中的水引到农田 P 处，如何挖掘能使渠道最短？
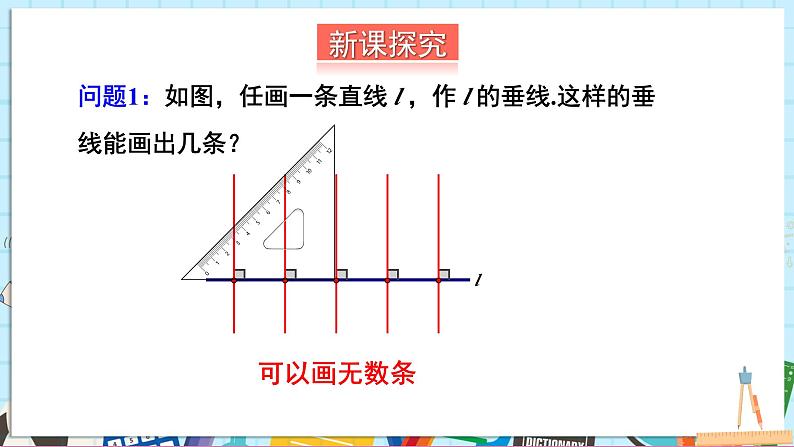
问题1：如图，任画一条直线 l ，作 l 的垂线.这样的垂线能画出几条？
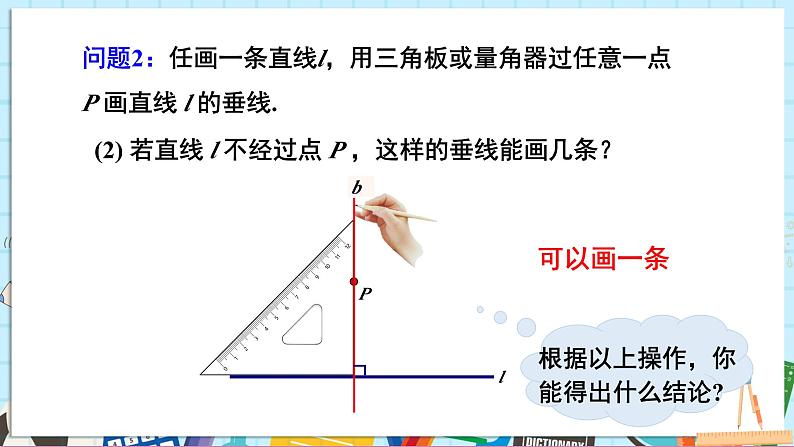
问题2：任画一条直线l，用三角板或量角器过任意一点 P 画直线 l 的垂线.
(1) 若直线 l 经过点 P ，这样的垂线能画几条？
(2) 若直线 l 不经过点 P ，这样的垂线能画几条？
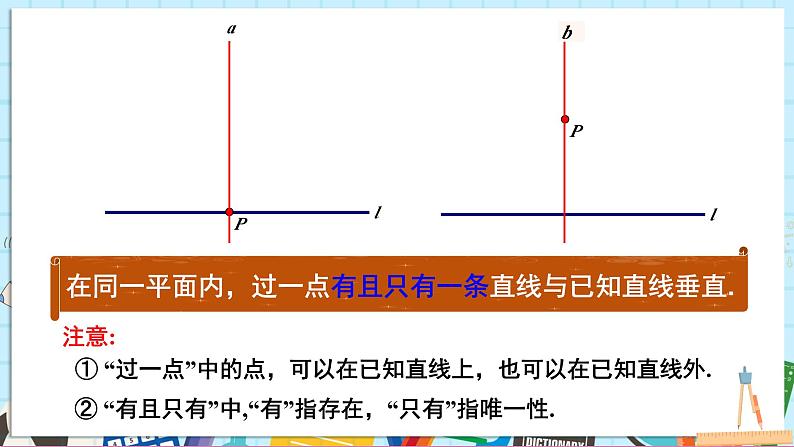
① “过一点”中的点，可以在已知直线上，也可以在已知直线外.
② “有且只有”中,“有”指存在，“只有”指唯一性.
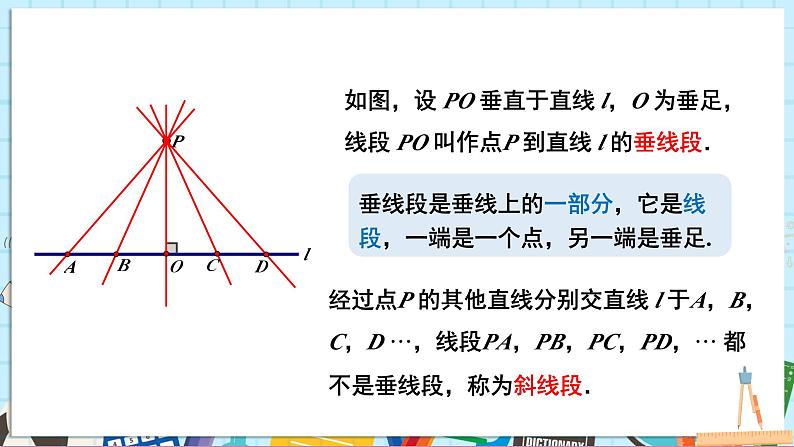
如图，设 PO 垂直于直线 l，O 为垂足，线段 PO 叫作点P 到直线 l 的垂线段．
经过点P 的其他直线分别交直线 l 于A，B，C，D ···，线段PA，PB，PC，PD，··· 都不是垂线段，称为斜线段．
垂线段是垂线上的一部分，它是线段，一端是一个点，另一端是垂足.
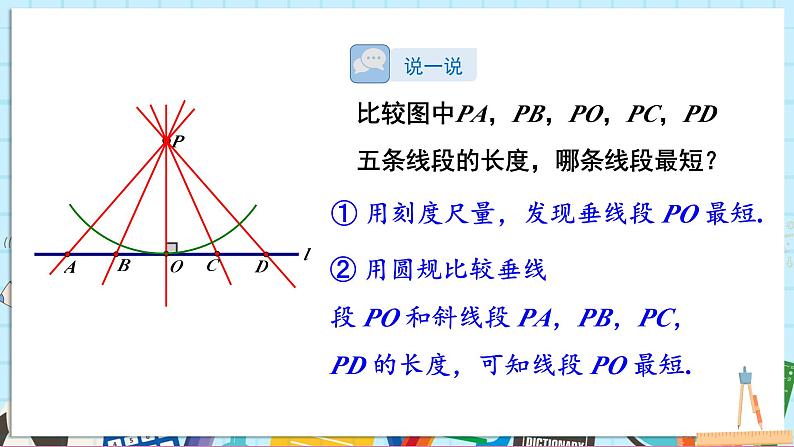
① 用刻度尺量，发现垂线段 PO 最短.
比较图中PA，PB，PO，PC，PD 五条线段的长度，哪条线段最短？
② 用圆规比较垂线段 PO 和斜线段 PA，PB，PC，PD 的长度，可知线段 PO 最短.
简单说成：垂线段最短．
如图：垂线段 PO 的长度叫作点 P 到直线 l 的距离.
特别规定：直线外一点与直线上各点连接的所有线段中，垂线段最短.
(1) 量出图中点 P 到直线 AB 的距离.
(2) 某单位要在河岸 l 上建一个水泵房引水到 C 处， 如图，问建在哪个位置才最节省水管？为什么？
(3) 由(1)(2)你会发现可以怎样求点到直线的距离？
求点到直线的距离可以转化为求点到点的距离.
解： 因为∠ABC = 90°，所以 AB⊥BC， 点B为垂足，所以线段 AB 即为点 A 到直线 BC 的垂线段.因为AB = 5，所以点 A 到直线 BC 的距离为 5.
解：因为 BD⊥AC， 垂足为点 D，所以线段 BD 的长度即为点 B 到直线 AC 的距离.
[选自教材P118 练习]
1. 如图，在△ ABC 中，∠A = 90 °，AB = 3 ，AC = 4 ，BC = 5 ，求点 A 到 BC 的距离，点 C 到 AB 的距离.
解: 作 AD ⊥ BC，垂足为点 D .
所以线段 AD 的长度即为点 A 到直线 BC 的距离.
因为∠BAC = 90°，所以 AC ⊥ AB， 点 A 为垂足，所以线段 AC 的长度即为点 C 到直线 AB 的距离，则距离为4.
提示: 用直尺量出图中点 P 到各直线的距离, 再按比例尺换算成实际距离.
2. 某公园的 4 条纵横交错的人行道和一喷泉的示意图如图所示（比例尺为：1∶5 000），其中直线 a，b，c，d表示人行道，点 P 表示喷泉. 量出点 P 到 4 条直线的距离，并求出其实际距离．
3．如图，体育课上应该怎样测量同学们的跳远成绩？
解: 体育课上，测量同学们的跳远成绩的方法: 先分别过落地点作起跳线的垂线，然后分别量取这些落地点到起跳线的垂线段的长度，这些长度就分别是同学们各自的跳远成绩.
1.如图，①过点 Q 作 QD⊥AB，垂足为 D，②过点 P 作 PE⊥AB，垂足为 E，③过点 Q 作 QF⊥AC，垂足为 F，④连 P、Q 两点，⑤ P、Q 两点间的距离是线段______的长度，⑥点 Q 到直线 AB 的距离是线段_______的长度，⑦点 Q 到直线 AC 的距离是线段_______的长度，⑧点 P 到直线 AB 的距离是线段________的长度.
解：①②③④ 作图如图所示
2. 如图，∠C = 90°，AB = 5，AC = 4，BC = 3，则点 A 到直线 BC 的距离为_____，点 B 到直线 AC 的距离为______，点A、B 间的距离为______.
3. 如图所示，火车站、码头分别位于A，B 两点，直线 a 和 b 分别表示河流与铁路.(1) 从火车站到码头怎样走最近，画图并说明理由；(2) 从码头到铁路怎样走最近，画图并说明理由；(3) 从火车站到河流怎样走最近，画图并说明理由.
解：如图所示:(1)沿AB 走，两点之间线段最短；(2)沿 BD 走，垂线段最短；(3)沿 AC 走，垂线段最短.
4.如图所示，已知∠AOB =∠COD = 90°，(1)若∠BOC = 45°，求∠AOC 与∠BOD 的度数；(2)若∠BOC = 25°，求∠AOC 与∠BOD 的度数；(3)由(1)、(2)你能得出什么结论？说说其中的道理.
解：(1)因为∠AOB =∠COD = 90°，且∠BOC = 45°，所以∠AOC =∠AOB-∠BOC = 45°，∠BOD =∠COD-∠BOC = 45°.(2)因为∠AOB =∠COD = 90°，且∠BOC = 25°，所以∠AOC =∠AOB-∠BOC = 65°，∠BOD =∠COD-∠BOC = 65°.(3)∠AOC =∠BOD，等角的余角相等.
5. 如图，OF 平分∠AOC，OE⊥OF，AB 与 CD 相交于 O，∠BOD = 130°，求∠EOB 的度数.
解：因为∠AOC =∠BOD，∠BOD = 130°，所以∠AOC = 130°.因为OF 平分∠AOC，所以∠AOF =∠FOC = 65°.因为OE⊥OF，所以∠EOF = 90°.所以∠BOE = 180°-∠AOF-∠EOF = 180°-65°-90°= 25°.
在同一平面内，过一点有且只有一条直线与已知直线垂直.