2025高考数学一轮复习-第2章-第8节 指数函数【课件】

这是一份2025高考数学一轮复习-第2章-第8节 指数函数【课件】，共52页。PPT课件主要包含了知识诊断自测，考点聚焦突破，BCD，课时分层精练，ABD等内容，欢迎下载使用。
1.通过实例，了解指数函数的实际意义，能用描点法或借助计算工具画出指数函数的图象.2.理解指数函数的单调性，特殊点等性质，并能简单应用.
ZHISHIZHENDUANZICE
1. 指数函数的概念函数y＝ax(a>0，且a≠1)叫做指数函数，其中指数x是自变量，定义域是R.
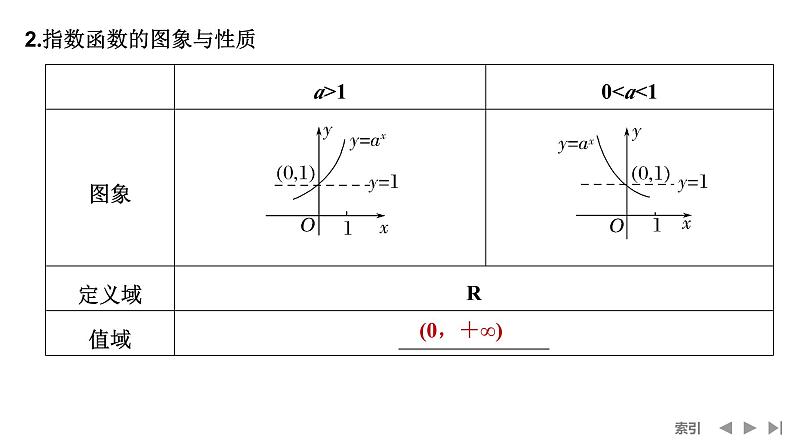
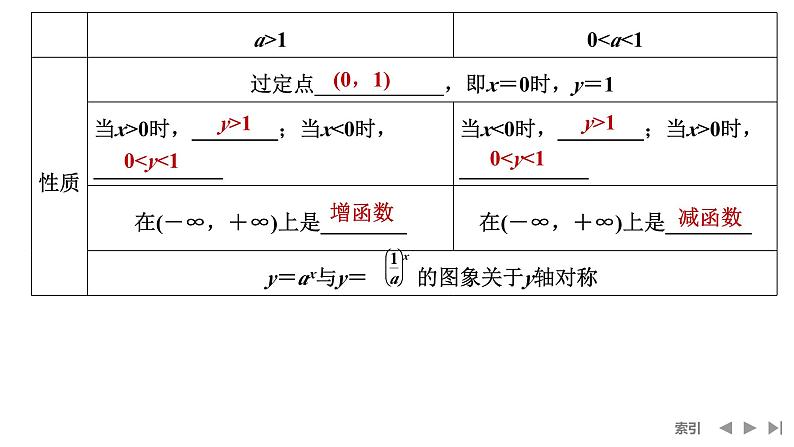
2.指数函数的图象与性质
(1)y＝ax，(2)y＝bx，(3)y＝cx，(4)y＝dx的图象，则c>d>1>a>b>0.
1.思考辨析(在括号内打“√”或“×”)(1)函数y＝2x－1是指数函数.(　　)(2)函数y＝ax2＋1(a>1)的值域是(0，＋∞).(　 )(3)2－3＞2－4.(　　)(4)若am＜an(a＞0，且a≠1)，则m＜n.(　　)
解析　(1)由于指数函数解析式为y＝ax(a＞0，且a≠1),故y＝2x－1不是指数函数,故(1)错误.(2)由于x2＋1≥1，又a＞1，∴ax2＋1≥a.故y＝ax2＋1(a＞1)的值域是[a，＋∞)，(2)错误.(4)m与n的大小关系与a的取值有关.
2.函数f(x)＝1－e|x|的图象大致是(　　)
解析　易知f(x)为偶函数，且f(x)＝1－e|x|≤0，A正确.
3.(必修一P119T6改编)已知a＝0.750.1，b＝1.012.7，c＝1.013.5，则(　　)A.a＞b＞c B.a＞c＞bC.c＞b＞a D.c＞a＞b
解析　因为函数y＝1.01x在(－∞，＋∞)上是增函数，且3.5＞2.7，故1.013.5＞1.012.7＞1＞0.750.1，即c＞b＞a.
{y|y＞0，且y≠1}
解析　函数的定义域为{x|x≠1}，
又指数函数y＝2x的值域为(0，＋∞)，故所求函数的值域为{y|y＞0，且y≠1}.
KAODIANJUJIAOTUPO
考点一　指数函数的图象及应用
例1 (1)函数f(x)＝ax－b的图象如图所示，其中a，b为常数，则下列结论正确的是(　　)
解析　由f(x)＝ax－b的图象可以观察出，函数f(x)＝ax－b在定义域上单调递减，所以0＜a＜1.又f(0)＝a－b＜a0，所以－b＞0，即b＜0.
A.a＞1，b＜0B.a＞1，b＞0C.0＜a＜1，b＞0D.0＜a＜1，b＜0
M(x1，y1)是y＝ex在x∈[0，1)图象上的动点，如图，B(1，e)，则k∈(－∞，－2]，只有B，C满足.
1.对于有关指数型函数的图象问题，一般是从最基本的指数函数的图象入手，通过平移、伸缩、对称变换得到.特别地，当底数a与1的大小关系不确定时应注意分类讨论.2.有关指数方程、不等式问题的求解，往往利用相应的指数型函数图象，数形结合求解.
解析　由题意得，f(x)的定义域为R，排除C，D；
(2)(2024·深圳质检)若直线y＝2a与函数y＝|ax－1|(a＞0，且a≠1)的图象有两个交点，则a的取值范围是____________.
解析　y＝|ax－1|的图象是由y＝ax的图象先向下平移1个单位长度，再将x轴下方的图象翻折到x轴上方，保持x轴上及其上方的图象不变得到的.
考点二　指数函数的性质及应用
角度1　比较大小例2 (1)(2023·天津卷)若a＝1.010.5，b＝1.010.6，c＝0.60.5，则a，b，c的大小关系为(　　)A.c>a>b B.c>b>aC.a>b>c D.b>a>c
解析　法一　因为函数f(x)＝1.01x是增函数，且0.6>0.5>0，所以1.010.6>1.010.5>1，即b>a>1；因为函数g(x)＝0.6x是减函数，且0.5>0，所以0.60.5c.
法二　因为函数f(x)＝1.01x是增函数，且0.6>0.5，所以1.010.6>1.010.5，即b>a；因为函数h(x)＝x0.5在(0，＋∞)上单调递增，且1.01>0.6>0，所以1.010.5>0.60.5，即a>c.综上，b>a>c.
(2)若ea＋πb≥e－b＋π－a，下列结论一定成立的是(　　)A.a＋b≤0 B.a－b≥0C.a－b≤0 D.a＋b≥0
解析　∵ea＋πb≥e－b＋π－a，∴ea－π－a≥e－b－πb，(*)令f(x)＝ex－π－x，则f(x)是R上的增函数，(*)式即为f(a)≥f(－b)，∴a≥－b，即a＋b≥0.
角度2　解简单的指数方程或不等式例3 已知y＝4x－3·2x＋3的值域为[1，7]，则x的取值范围是(　　)A.[2，4] B.(－∞，0)C.(0，1)∪[2，4] D.(－∞，0]∪[1，2]
解析　∵y＝4x－3·2x＋3的值域为[1，7]，∴1≤4x－3·2x＋3≤7，且2x＞0，∴0＜2x≤1或2≤2x≤4，∴x≤0或1≤x≤2.
因为f(x)是奇函数，所以f(－x)＝－f(x)，
(2)若∀x∈[1，2]，都有f(2x)－mf(x)≥0成立，求实数m的取值范围.
1.比较指数式的大小的方法是：(1)能化成同底数的先化成同底数幂，再利用单调性比较大小；(2)不能化成同底数的，一般引入“0或1”等中间量比较大小.2.指数方程(不等式)的求解主要利用指数函数的单调性进行转化.3.涉及指数函数的综合问题，首先要掌握指数函数相关性质，其次要明确复合函数的构成，涉及值域、单调区间、最值等问题时，都要借助“同增异减”这一性质分析判断.易错警示　在研究指数型函数的单调性时，当底数a与“1”的大小关系不确定时，要分类讨论.
解析　因为y＝1.7x为增函数，所以1.72.51，而0.93.1∈(0，1)，所以1.70.3>0.93.1，故C正确；
所以函数f(x)在(－∞，0)上单调递减，故A错误；
所以f(x)的图象关于y轴对称，故B正确；
故函数f(x)的图象不关于点(0，1)对称，故C错误；
KESHIFENCENGJINGLIAN
解析　由题意得2a2－5a＋3＝1，
当a＝2时，f(x)＝2x在(0，＋∞)上单调递增，符合题意；
综上所述，a＞b＞c.
∴根据指数函数图象即可判断选项C符合.
解析　函数f(x)的定义域为R.
则g(x)＝f(x)－3，
因为f(a2)＋f(3a－4)>6，所以f(a2)－3＋f(3a－4)－3>0，所以g(a2)＋g(3a－4)>0，即g(a2)>－g(3a－4)＝g(4－3a)，所以a2>4－3a，解得a1，故a的取值范围为(－∞，－4)∪(1，＋∞).故选D.
解析　法一　f(x)的定义域为(－∞，0)∪(0，＋∞)，因为f(x)为奇函数，所以f(－x)＝－f(x)，
法二　f(x)的定义域为(－∞，0)∪(0，＋∞)，因为f(x)为奇函数，所以f(－1)＝－f(1)，
所以当a＝1时，f(x)为奇函数.
解析　设2x＝t，0≤x≤2，则1≤t≤4，
10.满足下列三个性质的一个函数f(x)＝__________________.①若xy>0，则f(x＋y)＝f(x)f(y)；②f(x)＝f(－x)；③f(x)在(0,＋∞)上单调递减.
即f(x)＝f(－x)成立.又f(x)在(0，＋∞)上单调递减，
所以x1－x20，所以(x1－x2)(x1＋x2－1)