2025高考数学一轮复习-第5章-第1节 平面向量的概念及线性运算【课件】

这是一份2025高考数学一轮复习-第5章-第1节 平面向量的概念及线性运算【课件】，共49页。PPT课件主要包含了知识诊断自测，考点聚焦突破，课时分层精练，ABC等内容，欢迎下载使用。
1.了解向量的实际背景. 2.理解平面向量的概念，理解两个向量相等的含义. 3.理解向量的几何表示. 4.掌握向量加法、减法的运算，并理解其几何意义. 5.掌握向量数乘的运算及其几何意义，理解两个向量共线的含义. 6.了解向量线性运算的性质及其几何意义.
ZHISHIZHENDUANZICE
3.共线向量定理向量a(a≠0)与b共线的充要条件是：存在唯一一个实数λ，使________.
解析　(2)若b＝0，则a与c不一定平行.(3)共线向量所在的直线可以重合，也可以平行，则A，B，C，D四点不一定在一条直线上.
解析　A错误，单位向量长度相等，但是方向不确定；B错误，由于只有方向，没有大小，故x轴、y轴不是向量；C正确，由于向量起点相同，但长度不相等或方向不同，所以终点不同；D正确，海拔、温度、角度只有大小，没有方向，故不是向量.
KAODIANJUJIAOTUPO
考点一　平面向量的概念
解析　方向相反的两个非零向量必定平行，所以方向相反的两个非零向量一定共线，故A正确；零向量是有方向的，其方向是任意的，故B错误；
两个向量起点相同，终点相同，则两个向量相等；但两个向量相等，不一定有相同的起点和终点，故C错误；
对于B，向量a与b平行，且a或b为零向量时，不满足条件，故B错误；对于C，因为向量是既有大小又有方向的量，所以任意两个向量都不能比较大小，故C错误；对于D，两个终点相同的向量，不一定是共线向量，故D错误.
考点二　平面向量的线性运算
解析　如图，取CD的中点G，连接BG，交AC于点H.∵BE∥DG，BE＝DG，∴四边形BEDG为平行四边形，∴BG∥DE.又E为AB的中点，∴AF＝FH，同理可得CH＝FH，
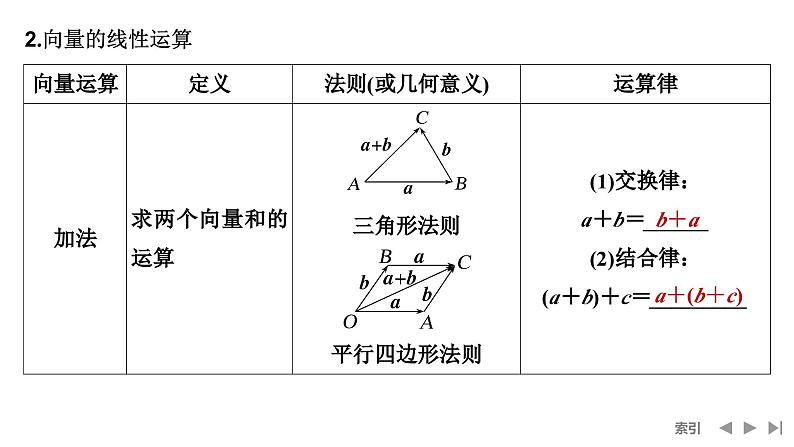
平面向量线性运算的常见类型及解题策略(1)向量求和用平行四边形法则或三角形法则；求差用向量减法的几何意义.(2)求参数问题可以通过向量的运算将向量表示出来，进行比较，求参数的值.
考点三　共线向量定理的应用
解析　因为c与d共线，所以存在k∈R，使得d＝kc，即a＋(2x－1)b＝kxa＋kb.
解析　在△ABC中，因为点M是BC的中点，
KESHIFENCENGJINGLIAN
1.化简2(a－3b)－3(a＋b)的结果为(　　)A.a＋4bB.－a－9bC.2a＋bD.a－3b
解析　2(a－3b)－3(a＋b)＝2a－6b－3a－3b＝－a－9b.
解析　对于A，当a，b之一为零向量时，不成立，故A错误；对于B，首尾顺次相接，B正确；对于C，两个单位向量互相平行，这两个单位向量相等或相反(大小相等，方向相反)，故C正确；对于D，当a＋b＝0时，零向量的方向是任意的，故D错误.
解析　因为四边形ABCD是边长为1的正方形，
在△ABC中，因为AD为BC边上的中线，所以D为BC的中点.
8.已知向量a，b不共线，且c＝λa＋2b，d＝a＋(2λ－3)b，若c与d反向共线，则实数λ的值为________.
解析　由于c与d反向共线，则存在实数k使c＝kd(k＜0)，于是λa＋2b＝k[a＋(2λ－3)b]，整理得λa＋2b＝ka＋(2λk－3k)b.
(2)证明：B，E，F三点共线.