2025高考数学一轮复习-第8章-第4节 直线与圆、圆与圆的位置关系【课件】

这是一份2025高考数学一轮复习-第8章-第4节 直线与圆、圆与圆的位置关系【课件】，共60页。PPT课件主要包含了知识诊断自测，考点聚焦突破，课时分层精练，BCD等内容，欢迎下载使用。
1.能根据给定直线、圆的方程判断直线与圆、圆与圆的位置关系.2.能用直线和圆的方程解决一些简单的数学问题与实际问题.
ZHISHIZHENDUANZICE
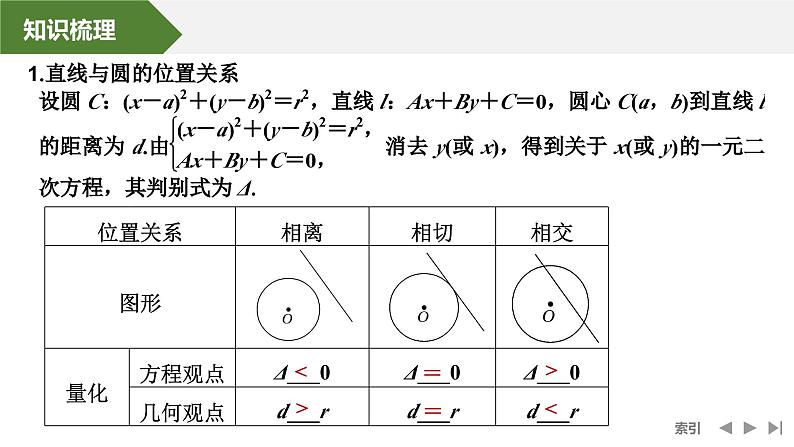
|r1－r2|0，所以直线l与圆相交.
法三(定点法)　直线l：mx－y＋1－m＝0，整理得m(x－1)－y＋1＝0过(1，1)，而12＋(1－1)20)；(2)与圆x2＋y2＋Dx＋Ey＋F＝0同心圆的圆系方程为x2＋y2＋Dx＋Ey＋λ＝0；(3)过直线Ax＋By＋C＝0与圆x2＋y2＋Dx＋Ey＋F＝0交点的圆系方程为x2＋y2＋Dx＋Ey＋F＋λ(Ax＋By＋C)＝0(λ∈R)；(4)过两圆C1：x2＋y2＋D1x＋E1y＋F1＝0，C2：x2＋y2＋D2x＋E2y＋F2＝0交点的圆系方程为x2＋y2＋D1x＋E1y＋F1＋λ(x2＋y2＋D2x＋E2y＋F2)＝0.(λ≠－1，此圆系不含C2：x2＋y2＋D2x＋E2y＋F2＝0)特别地，当λ＝－1时，上述方程为一次方程，两圆相交时，表示公共弦所在直线方程；两圆相切时，表示公切线所在直线方程.
一、直线系方程例1 (1)过点A(1，－4)且与直线2x＋3y＋5＝0平行的直线方程为________________.
解析　设所求直线方程为2x＋3y＋c＝0(c≠5)，由题意知2×1＋3×(－4)＋c＝0，解得c＝10，故所求直线方程为2x＋3y＋10＝0.
(2)经过点A(2，1)且与直线2x＋y－10＝0垂直的直线l的方程为________________.
解析　因为所求直线与直线2x＋y－10＝0垂直，所以设该直线方程为x－2y＋c＝0.又直线过点A(2，1)，所以有2－2×1＋c＝0，解得c＝0，故所求直线方程为x－2y＝0.
(3)已知两条直线l1：x－2y＋4＝0和l2：x＋y－2＝0的交点为P，过点P且与直线l3：3x－4y＋5＝0垂直的直线l的方程为________________.
解析　设所求直线l的方程为x－2y＋4＋λ(x＋y－2)＝0，即(1＋λ)x＋(λ－2)y＋4－2λ＝0.因为直线l与l3垂直，所以3(1＋λ)－4(λ－2)＝0，所以λ＝11，所以直线l的方程为4x＋3y－6＝0.
二、圆系方程例2 已知点M(2，－2)，圆O：x2＋y2＝3(O为坐标原点).(1)求经过M，以及圆O与圆x2＋y2＋3x＝0交点的圆的方程；
解　设圆的方程为x2＋y2＋3x＋λ(x2＋y2－3)＝0，
所求圆的方程是3x2＋3y2－5x－14＝0.
(2)过点M向圆O引两条切线，切点分别为A，B，求直线AB的方程.
解　以MO为直径的圆C的方程为x2＋y2－2x＋2y＝0，则由圆系方程可知圆C与圆O方程相减即得直线AB的方程为2x－2y＝3，或由切点弦的公式可直接得到2x－2y＝3.
训练 (1)过点P(－1，4)，与圆(x－2)2＋(y－3)2＝1相切的切线方程为_______________________.
y＝4或3x＋4y－13＝0
解析　因为切线过点P(－1，4)，故可设所求直线的方程为A(x＋1)＋B(y－4)＝0(其中A，B不全为零)，∵直线l与圆相切，∴圆心(2，3)到直线l的距离等于半径1，
(2)经过直线2x－y＋3＝0与圆x2＋y2＋2x－4y＋1＝0的两个交点，且面积最小的圆的方程是___________________.
(3)直线l1：x＋y－4＝0与l2：x－y＋2＝0的交点为P，直线l：2x－y－1＝0.求：①过点P且与直线l平行的直线方程；②过点P且与直线l垂直的直线方程.
所以l1与l2的交点为P(1，3).①设所求直线方程为2x－y＋c＝0(c≠－1)，则2－3＋c＝0，所以c＝1，所以所求直线方程为2x－y＋1＝0.②设与直线2x－y－1＝0垂直的直线方程为x＋2y＋c′＝0，则1＋2×3＋c′＝0，所以c′＝－7，所以所求直线方程为x＋2y－7＝0.
KESHIFENCENGJINGLIAN
1.已知直线l：x＋y－2＝0与圆C：x2＋y2＝2，点A(1，1)，则下列说法正确的是(　　)A.点A在圆C上，直线l与圆C相切B.点A在圆C内，直线l与圆C相离C.点A在圆C外，直线l与圆C相切D.点A在圆C上，直线l与圆C相交
所以直线l与圆C相切.因为点A(1，1)满足圆C的方程，所以点A在圆C上.
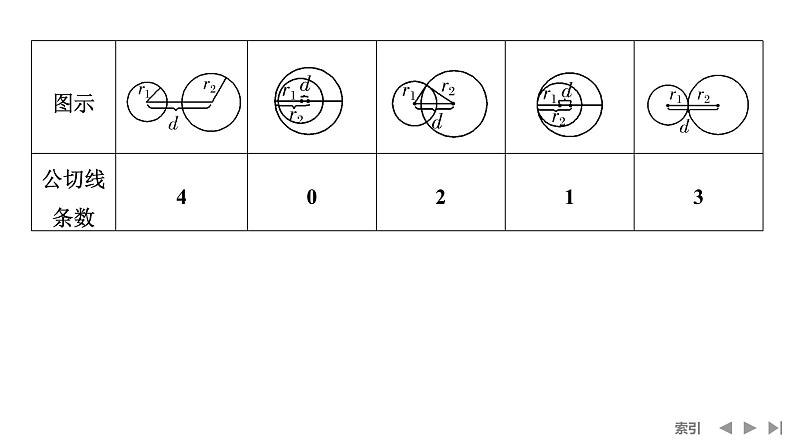
2.已知圆O1：(x－1)2＋(y＋2)2＝9，圆O2：(x＋2)2＋(y＋1)2＝16，则这两个圆的位置关系为(　　)A.外离B.外切C.相交D.内含
解析　圆x2＋y2＝4的圆心为(0，0)，半径r＝2，
4.圆x2＋2x＋y2＋4y－3＝0上到直线x＋y＋1＝0的距离为的点共有(　　)A.1个B.2个C.3个D.4个
解析　由题可得，圆心C(－1，－2)，|AC|＝2，且PA⊥AC，所以|PA|2＝|PC|2－4.要使|PA|最小，需|PC|最小.|PC|的最小值为点C到直线l的距离，
解析　因为圆M：(x－k2)2＋(y－2k)2＝3与圆N：(x－1)2＋y2＝1交于A，B两点，所以两圆方程相减，可得直线AB的方程为2(1－k2)x－4ky＋k4＋4k2－3＝0.
令k4＋2k2＝t，则t2＝3t，解得t＝0或t＝3，故k＝0或k＝±1.经检验k＝0，1，－1满足上式.
7.(多选)(2024·南京调研)已知圆C：(x－a)2＋(y－b)2＝1，则下列说法正确的是(　　　)A.若圆C与两坐标轴均相切，则a＝bB.若a＝b，则圆C不可能过点(0，2)C.若点(3，4)在圆C上，则圆心C到原点O的距离的最小值为4D.若圆C上有两点到原点的距离为1，则0