2025高考数学一轮复习-第9章-第3节 成对数据的统计分析【课件】

这是一份2025高考数学一轮复习-第9章-第3节 成对数据的统计分析【课件】，共60页。PPT课件主要包含了知识诊断自测，ABC，考点聚焦突破，考点二回归分析，考点三独立性检验，课时分层精练，ACD等内容，欢迎下载使用。
1.了解样本相关系数的统计含义. 2.了解一元线性回归模型和2×2列联表，会运用这些方法解决简单的实际问题.
ZHISHIZHENDUANZICE
1.变量的相关关系(1)相关关系的分类：正相关和负相关.(2)线性相关：一般地，如果两个变量的取值呈现正相关或负相关，而且散点落在__________附近，我们就称这两个变量线性相关.一般地，如果两个变量具有相关性，但不是线性相关，那么我们就称这两个变量非线性相关或曲线相关.
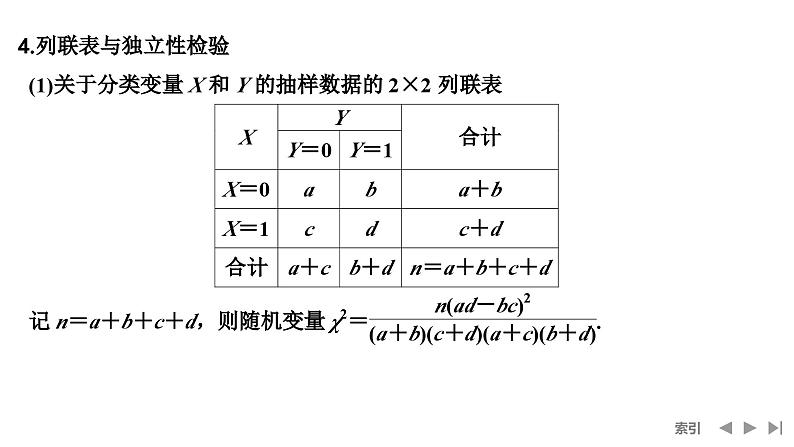
(2)独立性检验基于小概率值α的检验规则是：当χ2≥xα时，我们就推断H0不成立，即认为X和Y不独立，该推断犯错误的概率不超过α；当χ2＜xα时，我们没有充分证据推断H0不成立 ，可以认为X和Y独立.下表给出了χ2独立性检验中几个常用的小概率值和相应的临界值
解析　(1)散点图是判断两个变量是否相关的一种重要方法和手段.(4)χ2的值越大，相关性越强，关系越密切.
2.(选修三P139T3)根据分类变量x与y的观测数据，计算得到χ2＝2.974.依据α＝0.05的独立性检验，结论为(　　)A.变量x与y不独立B.变量x与y不独立，这个结论犯错误的概率不超过0.05C.变量x与y独立D.变量x与y独立，这个结论犯错误的概率不超过0.05
解析　由χ2＝2.9740.75，所以花瓣长度和花萼长度的相关性较强，并且呈正相关，所以选项A，B错误，选项C正确；因为相关系数与样本的数据有关，所以当样本发生变化时，相关系数也会发生变化，所以选项D错误.故选C.
(2)(2024·杭州质检)某兴趣小组研究光照时长x(h)和向日葵种子发芽数量y(颗)之间的关系，采集5组数据，作如图所示的散点图.若去掉D(10，2)，则下列说法正确的是(　　)A.相关系数r变小B.决定系数R2变小C.残差平方和变大D.解释变量x与预报变量y的相关性变强
解析　可知点D偏离程度较大，去掉点D后，相关系数r变大，决定系数R2变大，残差平方和变小，解释变量x与预报变量y的相关性变强.故选D.
判定两个变量相关性的方法(1)画散点图：点的分布从左下角到右上角，两个变量正相关；点的分布从左上角到右下角，两个变量负相关.(2)样本相关系数：当r＞0时，正相关；当r＜0时，负相关；|r|越接近于1，相关性越强.(3)决定系数法：利用决定系数判定，R2越接近1，模型的拟合效果越好，相关性越强.
训练1 (1)(2023·上海卷)已知某校50名学生的身高与体重的散点图如图所示，则下列说法正确的是(　　)A.身高越高，体重越重B.身高越高，体重越轻C.身高与体重成正相关D.身高与体重成负相关
解析　由题图可知，身高越高的体重不一定就越重或越轻，但总体上来说，样本学生的身高和体重之间具有明显的相关性，个子高的学生往往更重一些，所以身高与体重成正相关.故选C.
角度1　线性回归分析例2 为实施乡村振兴，科技兴农，某村建起了田园综合体，并从省城请来专家进行技术指导，根据统计，该田园综合体西红柿亩产量的增加量y(千克)与某种液体肥料每亩使用量x(千克)之间的对应数据如下：
(1)由上表数据可知，可用经验回归模型拟合y与x的关系，请计算样本相关系数r并加以说明(若|r|＞0.75，则线性相关程度很高，可用经验回归模型拟合)；
回归分析问题的类型及解题方法(1)求经验回归方程①当两个系数均未知时，可利用公式法求解；②当两个系数已知一个求另一个时，可利用经验回归直线过样本点的中心求解.(2)利用经验回归方程进行预测，把经验回归方程看作一次函数，求函数值.(3)经验回归方程的拟合效果可以利用相关系数判断，当|r|越趋近于1时，两变量的线性相关性越强.
训练2 (2024·西安调研)某商业银行对存款利率与日存款总量的关系进行调研，发现存款利率每上升一定的百分点，日均存款总额就会发生一定的变化，经过统计得到下表：
(1)在给出的坐标系中画出上表数据的散点图；
解　设利率需上升x个百分点，由(2)得，0.625×2＝1.5x＋0.05，解得x＝0.8，所以预测利率需上升0.8个百分点.
例4 (2023·全国甲卷改编)一项试验旨在研究臭氧效应，试验方案如下：选40只小白鼠，随机地将其中20只分配到试验组，另外20只分配到对照组，试验组的小白鼠饲养在高浓度臭氧环境，对照组的小白鼠饲养在正常环境，一段时间后统计每只小白鼠体重的增加量(单位：g).试验结果如下：对照组的小白鼠体重的增加量从小到大排序为15.2　18.8　20.2　21.3　22.5　23.2　25.826.5　27.5　30.1　32.6　34.3　34.8　35.635.6　35.8　36.2　37.3　40.5　43.2试验组的小白鼠体重的增加量从小到大排序为7.8　9.2　11.4　12.4　13.2　15.5　16.518.0　18.8　19.2　19.8　20.2　21.6　22.823.6　23.9　25.1　28.2　32.3　36.5
(1)计算试验组的样本平均数；
(2)①求40只小白鼠体重的增加量的中位数m，再分别统计两样本中小于m与不小于m的数据的个数，完成如下列联表：
解　零假设为H0：小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量没有差异.
依据小概率值α＝0.050的独立性检验，我们推断H0不成立，所以在犯错误的概率不超过0.050的前提下，即认为小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量有差异.
训练3 某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次，整理数据得到下表(单位：天)：
(1)分别估计该市一天的空气质量等级为1，2，3，4的概率；
解　由所给数据，得该市一天的空气质量等级为1，2，3，4的概率的估计值如下表：
(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表)；
解　根据所给数据，可得2×2列联表：
零假设为H0：一天中到该公园锻炼的人次与该市当天的空气质量无关.
根据小概率值α＝0.050的独立性检验，可推断H0不成立，所以在犯错误的概率不超过0.050的前提下，可认为一天中到该公园锻炼的人次与该市当天的空气质量有关.
KESHIFENCENGJINGLIAN
1.某机构为调查网游爱好者是否有性别差异，通过调研数据统计：在500名男生中有200名爱玩网游，在400名女生中有50名爱玩网游.若要确定网游爱好是否与性别有关时，用下列最适合的统计方法是(　　)A.均值B.方差C.独立性检验D.回归分析
解析　由题意可知，“爱玩网游”与“性别”是两类变量，其是否有关，应用独立性检验判断.
解析　r的绝对值越大，m越小，线性相关性越强.
解析　根据题表中的数据，由题意得
7.(多选)为了解阅读量多少与幸福感强弱之间的关系，一个调查机构根据所得到的数据，绘制了如下所示的2×2列联表(个别数据暂用字母表示)：
计算得：χ2≈12.981，参照下表：
对于下面的选项，正确的是(　　)A.根据小概率值α＝0.010的独立性检验，可以认为“阅读量多少与幸福感强弱无关”B.m＝54C.根据小概率值α＝0.005的独立性检验，可以在犯错误的概率不超过0.5%的前提下认为“阅读量多少与幸福感强弱有关”D.n＝52
解析　∵χ2≈12.981＞7.879＞6.635，∴根据小概率值α＝0.010的独立性检验，可以在犯错误的概率不超过1%的前提下认为“阅读量多少与幸福感强弱有关”，根据小概率值α＝0.005的独立性检验，可以在犯错误的概率不超过0.5%的前提下认为“阅读量多少与幸福感强弱有关”，∴A错，C正确，∵m＋36＝90，18＋n＝60，∴m＝54，n＝42，∴B正确，D错.
10.一项研究同年龄段的男、女生的注意力差别的脑功能实验，其实验数据如表所示：
则χ2＝________(精确到小数点后三位)，依据概率值α＝0.05的独立性检验，该实验______该年龄段的学生在注意力的稳定性上对于性别没有显著差异(填拒绝或支持).
解析　由表中数据可知a＝29，b＝7，c＝33，d＝5，n＝a＋b＋c＋d＝74，
所以没有充分证据认为学生在注意力的稳定性上与性别有关，即该实验支持该年龄段的学生在注意力的稳定性上对于性别没有显著差异.
(2)该企业改进生产工艺后，生产了批次乙的芯片.某手机厂商获得批次甲与批次乙的芯片，并在某款手机上使用.现对使用这款手机的100名用户回访，对开机速度进行调查.据统计，安装批次甲的有40名，其中对开机速度满意的有30名；安装批次乙的有60名，其中对开机速度满意的有55名.试整理出2×2列联表(单位：名)，并依据小概率值α＝0.05的独立性检验，分析芯片批次是否与用户对开机速度满意有关.
解　零假设为H0：芯片批次与用户对开机速度满意无关，得2×2列联表如下：
所以依据α＝0.05的独立性检验，我们推断H0不成立，所以认为芯片批次与用户对开机速度满意有关，此推断犯错误的概率不大于0.05.
(1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量；
(2)求该林区这种树木的根部横截面积与材积量的样本相关系数(精确到0.01)；
解　设该林区这种树木的总材积量的估计值为Y m3，又已知树木的材积量与其根部横截面积近似成正比，
解析　对于A，由题图知，海拔高度越高，大气压强越小，所以大气压强与海拔高度负相关，故A正确；对于B，经验回归直线得到的数据为估计值，而非精确值，故B错误；
14.(2024·厦门质检)移动物联网广泛应用于生产制造、公共服务、个人消费等领域.截至2023年底，我国移动物联网连接数达18.45亿户，成为全球主要经济体中首个实现“物超人”的国家.如图是2019～2023年移动物联网连接数W与年份代码t的散点图，其中年份2019～2023对应的t分别为1～5.
(1)根据散点图推断两个变量是否线性相关.计算样本相关系数(精确到0.01)，并推断它们的相关程度；
解　由散点图可以看出样本点都集中在一条直线附近，由此推断两个变量线性相关.