2025高考数学一轮复习-第10章-第9节 概率与统计的综合问题【课件】

这是一份2025高考数学一轮复习-第10章-第9节 概率与统计的综合问题【课件】，共60页。PPT课件主要包含了所以X的分布列为，感悟提升，则X的分布列为，课时分层精练，列联表如下等内容，欢迎下载使用。
1.会从统计图表中提取有效信息，用以解决概率问题. 2.能够解决概率与回归分析、独立性检验的综合问题．
考点一　统计图表与概率
例1 (12分)为了解决家长接送孩子放学的问题，教育部提出推行课后服务“5＋2”模式，即学校每周5天都要开展课后服务，每天至少开展2 h，结束时间要与当地正常下班时间相衔接，且不得利用课后服务时间讲新课.为了课后服务的有序开展，某教育局就课后服务的时长在网络上进行意见征集，并从中随机抽取了100份调查表，以此为样本绘制了如图所示的频率分布直方图：
(1)从样本中随机抽取2份调查表，若其中一份调查表所建议的课后服务时长超过200 min，求另一份调查表所建议的课后服务时长也超过200 min的概率；(2)为了进一步了解课后服务时长的需求情况，从样本中建议课后服务时长超过180 min的人中分层抽取10人，再从这10人中任取3人，记建议课后服务时长在[180，200)的人数为X，求X的分布列与数学期望.[思路分析]　(1)先根据频率分布直方图求出课后服务时长超过200 min的调查表份数，再设出相关事件并求概率，最后根据条件概率的概率计算公式求解即可；(2)先根据题意及分层随机抽样的知识求出X的所有可能取值，然后求解相应的概率，列出分布列，求得数学期望.
[规范解答]　解　(1)依题意，课后服务时长超过200 min的调查表共有100×(0.007 5＋0.002 5)×20＝20(份)①，(1分)设事件A为其中一份调查表所建议的课后服务时长超过200 min，事件B为另一份调查表所建议的课后服务时长也超过200 min，
(2)根据题意及分层随机抽样的知识可知，抽取的10人中，建议课后服务时长在[180，200)内的有6人，则X的所有可能取值为0，1，2，3④，(7分)
[满分规则]❶得步骤分①②⑤每列一个式子并计算正确可得1分；❷得关键分③是条件概率公式得2分，④随机变量取值不要多写也不能漏写；❸得计算分⑥正确计算期望可得2分.
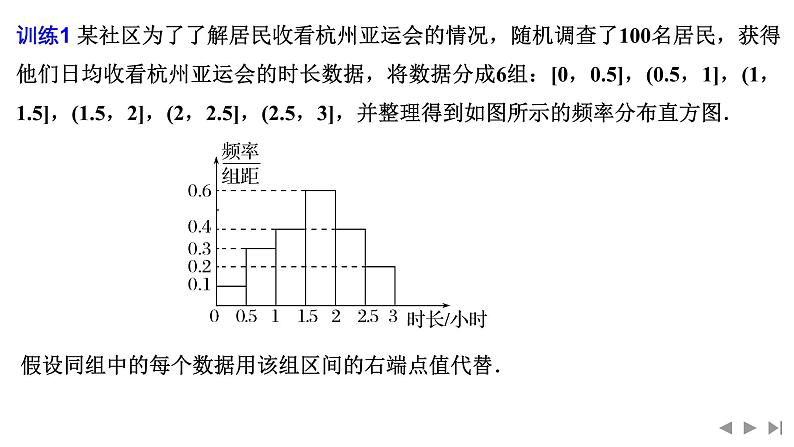
训练1 某社区为了了解居民收看杭州亚运会的情况，随机调查了100名居民，获得他们日均收看杭州亚运会的时长数据，将数据分成6组：[0，0.5]，(0.5，1]，(1，1.5]，(1.5，2]，(2，2.5]，(2.5，3]，并整理得到如图所示的频率分布直方图．
假设同组中的每个数据用该组区间的右端点值代替．
(1)试估计该社区居民日均收看杭州亚运会的时长的平均值；
解　根据题意，估计该社区居民日均收看杭州亚运会的时长的平均值为(0.5×0.1＋1×0.3＋1.5×0.4＋2×0.6＋2.5×0.4＋3×0.2)×0.5＝1.875小时．
(2)以频率估计概率，从该社区居民中随机抽取3人，以X表示其中日均收看杭州亚运会的时长在(1.5，2.5]的居民人数，求X的分布列和数学期望E(X)；
解　由条件可知，从该社区居民中随机抽取1人，其日均收看杭州亚运会的时长在(1.5，2.5]的概率估计为(0.6＋0.4)×0.5＝0.5，
(3)经过进一步调查发现，这100名居民收看杭州亚运会的方式有：①收看新闻或收看比赛集锦，②收看比赛转播或到现场观看．他们通过这两种方式收看的日均时长与其日均收看杭州亚运会的时长的比值如下表：
日均收看杭州亚运会的时长在[0，0.5]，(0.5，1.5]，(1.5，3]的居民通过方式①收看的平均时长分别记为μ1，μ2，μ3，写出μ1，μ2，μ3的大小关系．(结论不要求证明)
解　μ1＝0.5×1＝0.5小时，因为(0.5，1]，(1，1.5]的人数之比为3∶4，
因为(1.5，2]，(2，2.5]，(2.5，3]的人数之比为3∶2∶1，
所以μ2＞μ3＞μ1.
考点二　回归分析与概率
(1)在所统计的5个年借阅量中任选2个，记其中低于平均值的个数为X，求X的分布列和数学期望E(X)；
所以模型①的残差平方和大于模型②的残差平方和，所以模型②的拟合效果更好.
高考常将回归模型与分布列等交汇在一起进行考查，求解时注意概率模型的应用，明确所求问题所属的事件类型是关键．
训练2 击鼓传花，也称传彩球，是中国古代传统民间酒宴上的助兴游戏，属于酒令的一种，又称“击鼓催花”，在唐代时就已出现．杜牧《羊栏浦夜陪宴会》诗句中有“球来香袖依稀暖，酒凸觥心泛艳光”，可以得知唐代酒宴上击鼓传花助兴的情景．游戏规则为：鼓响时，开始传花(或一小物件)，鼓响时众人开始依次传花，至鼓停为止，此时花在谁手中(或其序位前)，谁就上台表演节目(多是唱歌、跳舞、说笑话或回答问题、猜谜、按纸条规定行事等)．某单位组织团建活动，9人一组，共9组，玩击鼓传花，组号x(前五组)与组内女性人数y统计结果如表：
若女性人数y与组号x(组号变量x依次为1，2，3，4，5，…)具有线性相关关系．
(2)从前5组中随机抽取3组，若3组中女性人数不低于3人的有X组，求X的分布列与期望．
解　由题可知X的所有可能取值为1，2，3，
考点三　独立性检验与概率
例3 (2024·广州模拟)某高校为调查学生性别与是否喜欢排球运动的关系，在全校范围内采用简单随机抽样的方法，分别抽取了男生和女生各100名作为样本，经统计，得到了如图所示的等高堆积条形图.
(1)根据等高堆积条形图，填写下列2×2列联表，并依据α＝0.001的独立性检验，是否可以认为该校学生的性别与是否喜欢排球运动有关联；
解　由等高堆积条形图知，2×2列联表为
高考常将独立性检验与分布列等交汇在一起进行考查，由2×2列联表解决相关问题，解题的关键是正确理解2×2列联表，能利用2×2列联表正确计算出各组数据．
训练3 (2024·杭州模拟)在杭州亚运会的志愿者选拔工作中，某高校承办了亚运会志愿者选拔的面试工作，面试成绩满分100分，现随机抽取了80名候选者的面试成绩分五组，第一组[45，55)，第二组[55，65)，第三组[65，75)，第四组[75，85)，第五组[85，95]，绘制成如图所示的频率分布直方图.已知图中从左到右前三个组的频率成等差数列，第一组和第五组的频率相同.
(1)求a，b的值，并估计这80名候选者面试成绩的平均值(同一组中的数据用该组区间的中点值作代表)和中位数(中位数精确到0.1)；
解　由题意知20b＝10a＋0.45，(2a＋b＋0.065)×10＝1，解得a＝0.005，b＝0.025，所以平均值为50×0.05＋60×0.25＋70×0.45＋80×0.2＋90×0.05＝69.5，
解　补全2×2列联表：
所以依据小概率值α＝0.05的独立性检验，我们推断H0不成立，即认为参加宁波赛区志愿者服务的候选人与性别有关.
解　X的所有可能取值为2，3，4，
微点突破　概率与函数、数列
在概率与统计的问题中，决策的工具是样本的数字特征或有关概率.决策方案的最佳选择是将概率最大(最小)或均值最大(最小)的方案作为最佳方案，这往往借助于函数、不等式、数列的有关性质去实现.
例1 某盒子内装有60个小球(除颜色之外其他完全相同)，其中有若干个黑球，其他均为白球.为了估计黑球的数目，设计如下实验：从盒子中有放回地抽取4个球，记录该次所抽取的黑球数目X，作为一次实验结果.进行上述实验共5次，记录下第i次实验中实际抽到黑球的数目xi.已知从该盒子中任意抽取一个球，抽到黑球的概率为p(0