专题7.1 平行线的判定【七大题型】-最新苏教版七年级下册数学精讲精练

这是一份专题7.1 平行线的判定【七大题型】-最新苏教版七年级下册数学精讲精练，文件包含专题71平行线的判定七大题型-最新苏教版七年级下册数学精讲精练教师版docx、专题71平行线的判定七大题型-最新苏教版七年级下册数学精讲精练学生版docx等2份试卷配套教学资源，其中试卷共35页， 欢迎下载使用。
1、注重生活联系，形式活泼多样。初中生的数学思维能力正逐步由直观形象思维向抽象思维发展。这个发展需要一定的过程。
2、注重动手操作，引导学生“做”数学。有效的数学学习活动不能单纯地依赖模仿与记忆，自主探索与合作交流也是学习数学的重要方法。
3、注重“过程”和数学思想方法。新教材通过让学生亲身经历知识的形成过程，使学生的学习过程更多地成为其发现数学、了解数学、体验数学的过程。
专题7.1 平行线的判定【七大题型】
【苏科版】
TOC \ "1-3" \h \u
\l "_Tc15185" 【题型1 平行公理及其推论】 PAGEREF _Tc15185 \h 1
\l "_Tc5524" 【题型2 同位角相等，两直线平行】 PAGEREF _Tc5524 \h 2
\l "_Tc26075" 【题型3 内错角相等，两直线平行】 PAGEREF _Tc26075 \h 4
\l "_Tc18821" 【题型4 同旁内角互补，两直线平行】 PAGEREF _Tc18821 \h 5
\l "_Tc3069" 【题型5 平行线的判定方法的综合运用】 PAGEREF _Tc3069 \h 6
\l "_Tc31586" 【题型6 角平分线与平行线的判定综合运用】 PAGEREF _Tc31586 \h 7
\l "_Tc19257" 【题型7 平行线判定的实际应用】 PAGEREF _Tc19257 \h 9
【知识点 平行线的判定】
1.平行公理及其推论
①经过直线外一点，有且只有一条直线与已知直线平行.
②如果两条直线都和第三条直线平行，那么这两条直线也互相平行.
2.平行线的判定方法
①两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.（同位角相等，两直线平行）.
②两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行. （内错角相等，两直线平行.
③两直线被第三条直线所截，如果同旁内角互补，则这两条直线平行.（同旁内角互补，两直线平行.）
【题型1 平行公理及其推论】
【例1】（2022·江西上饶·七年级期中）同一平面内的四条直线若满足a⊥b，b⊥c，c⊥d，则下列式子成立的是（ ）
A．a∥dB．b⊥dC．a⊥dD．b∥c
【变式1-1】（2022·河南漯河·七年级期末）如图，工人师傅用角尺画出工件边缘AB的垂线a和b，得到a∥b，理由是（ ）
A．连接直线外一点与直线上各点的所有线段中，垂线段最短
B．在同一平面内，垂直于同一条直线的两条直线互相平行
C．在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线
D．经过直线外一点，有且只有一条直线与这条直线平行
【变式1-2】（2022·湖北武汉·七年级期中）下列命题：①内错角相等；②两个锐角的和是钝角；③ a ， b ， c 是同一平面内的三条直线，若a//b，b// c ，则a// c ；④ a ， b ， c 是同一平面内的三条直线，若a  b ， b  c ，则a  c ； 其中真命题的个数是（ ）
A．1个B．2 个C．3 个D．4 个
【变式1-3】（2022·四川·甘孜藏族自治州教育局七年级期末）如图， AB∥CD， 如果∠1=∠2， 那么EF与AB平行吗？ 说说你的理由． 解：因为∠1=∠2，
所以____________∥___________．（ ）
又因为AB∥CD，
所以AB∥EF． （ ）
【题型2 同位角相等，两直线平行】
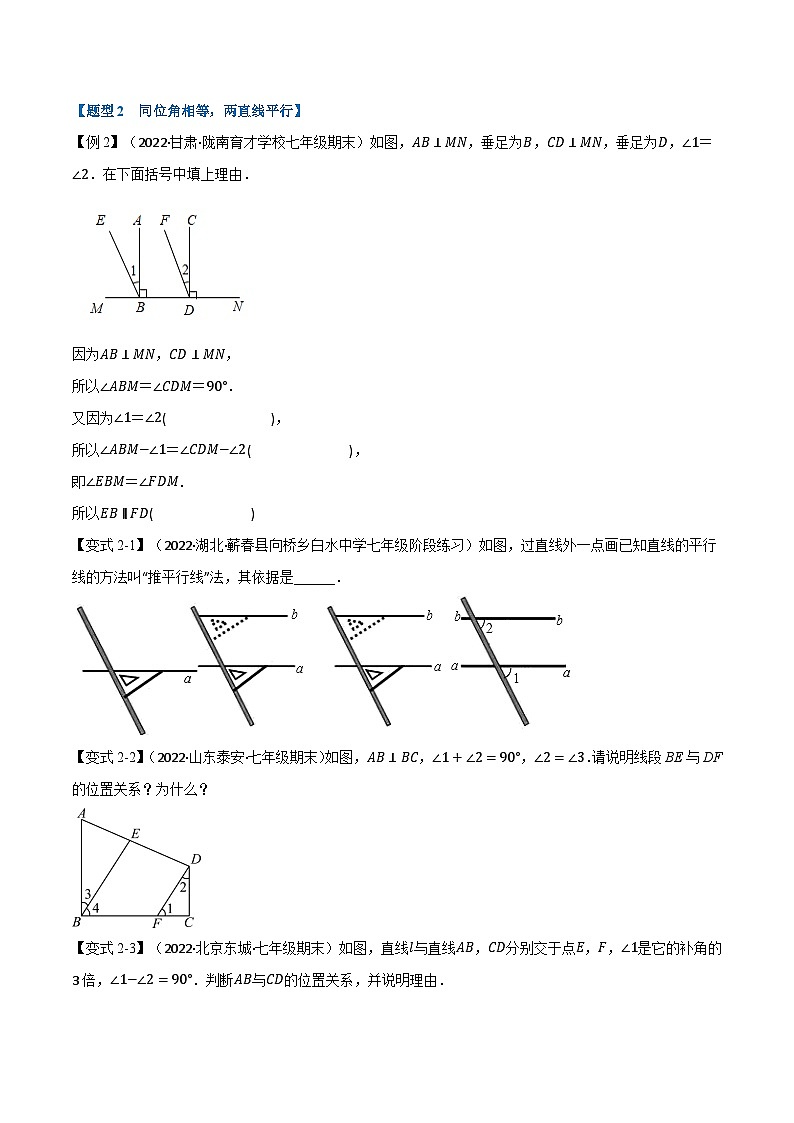
【例2】（2022·甘肃·陇南育才学校七年级期末）如图，AB⊥MN，垂足为B，CD⊥MN，垂足为D，∠1＝∠2．在下面括号中填上理由．
因为AB⊥MN，CD⊥MN，
所以∠ABM＝∠CDM＝90°．
又因为∠1＝∠2( )，
所以∠ABM−∠1＝∠CDM−∠2( )，
即∠EBM＝∠FDM．
所以EB∥FD( )
【变式2-1】（2022·湖北·蕲春县向桥乡白水中学七年级阶段练习）如图，过直线外一点画已知直线的平行线的方法叫“推平行线”法，其依据是______．
【变式2-2】（2022·山东泰安·七年级期末）如图，AB⊥BC，∠1+∠2=90°，∠2=∠3．请说明线段BE与DF的位置关系？为什么？
【变式2-3】（2022·北京东城·七年级期末）如图，直线l与直线AB，CD分别交于点E，F，∠1是它的补角的3倍，∠1−∠2=90°．判断AB与CD的位置关系，并说明理由．
【题型3 内错角相等，两直线平行】
【例3】（2022·山东·曲阜九巨龙学校七年级阶段练习）如图，点A在直线DE上，AB⊥AC于A，∠1与∠C互余，DE和BC平行吗？若平行，请说明理由．
【变式3-1】（2022·北京市房山区燕山教委八年级期中）如图，已知∠1=75°，∠2=35°，∠3=40°，求证：a∥b．
【变式3-2】（2022·福建·莆田第二十五中学八年级阶段练习）如图，CF是△ABC外角∠ACM的平分线，∠ACB=40°，∠A=70°，求证：AB∥CF.
【变式3-3】（2022·辽宁·阜新市第十中学七年级期中）如图，AB∥DE，∠1=∠ACB，∠CAB=12∠BAD，试说明AD∥BC．
【题型4 同旁内角互补，两直线平行】
【例4】（2022·河北衡水·七年级阶段练习）已知：∠A=∠C=120°，∠AEF=∠CEF=60°，求证：AB∥CD．
【变式4-1】（2022·西藏昂仁县中学七年级期中）如图，∠CAD＝20°，∠B＝70°，AB⊥AC，求证：AD∥BC．
【变式4-2】（2022·甘肃·平凉市第七中学七年级期中）如图，∠1=30°,∠B=60°,AB⊥AC.
(1) ∠DAB+∠B等于多少度？
(2)AD与BC平行吗？请说明理由．
【变式4-3】（2022·北京市第五中学分校七年级期末）如图，已知点E在BC上，BD⊥AC，EF⊥AC，垂足分别为D，F，点M，G在AB上，GF交BD于点H，∠BMD+∠ABC＝180°，∠1＝∠2，求证：MD∥GF．
下面是小颖同学的思考过程，请补全证明过程并在括号内填上证明依据．
证明：∵BD⊥AC，EF⊥AC，
∴∠BDC＝90°，∠EFC＝90°（① ）．
∴∠BDC＝∠EFC（等量代换）．
∴BD∥EF（同位角相等，两直线平行）．
∴∠2＝∠CBD（ ② ）．
∵∠1＝∠2（已知）．
∴∠1＝∠CBD（等量代换）．
∴③ （内错角相等，两直线平行）．
∵∠BMD+∠ABC＝180°（已知），
∴MD∥BC（④ ）．
∴MD∥GF（⑤ ）．
【题型5 平行线的判定方法的综合运用】
【例5】（2022·广西贺州·七年级期末）如图，有下列条件：①∠1=∠2；②∠3+∠4=180°；③∠5+∠6=180°；④∠2=∠3．其中，能判断直线a∥b的有（ ）
A．4个B．3个C．2个D．1个
【变式5-1】（2022·浙江台州·七年级期末）在铺设铁轨时，两条直轨必须是互相平行的，如图，已经知道∠2是直角，那么再度量图中已标出的哪个角，不能判断两条直轨是否平行( )
A．∠1B．∠3C．∠4D．∠5
【变式5-2】（2022·山西临汾·七年级期末）在下列图形中，已知∠1=∠2，一定能推导出l1∥l2的是（ ）
A．B．C．D．
【变式5-3】（2022·山东日照·七年级期末）如图，在下列给出的条件中，不能判定DE∥BC的是（ ）
A．∠1=∠2B．∠3=∠4C．∠5=∠CD．∠B+∠BDE=180°
【题型6 角平分线与平行线的判定综合运用】
【例6】（2022·吉林·大安市乐胜乡中学校七年级阶段练习）如图，在四边形ABCD中，∠ADC+∠ABC=180°，∠ADF+∠AFD=90°，点E、F分别在DC、AB上，且BE、DF分别平分∠ABC、∠ ADC，判断BE、DF是否平行，并说明理由．
【变式6-1】（2022·江苏·扬州市邗江区实验学校七年级期末）将下列证明过程补充完整：
已知：如图，点E在AB上，且CE平分∠ACD，∠1＝∠2．求证：AB∥CD．
证明：∵CE平分∠ACD（已知），
∴∠2＝∠ （ ）．
∵∠1＝∠2（已知），
∴∠1＝∠ （ ）．
∴AB∥CD（ ）．
【变式6-2】（2022·辽宁沈阳·七年级期末）按逻辑填写步骤和理由，将下面的证明过程补充完整
如图，直线MN分别与直线AC、DG交于点B、F，且∠1＝∠2．∠ABF的角平分线BE交直线DG于点E，∠BFG的角平分线FC交直线AC于点C．
求证：BE∥CF．
证明：∵∠1＝∠2（已知）
∠ABF＝∠1（对顶角相等）
∠BFG＝∠2（____________）
∴∠ABF＝______（等量代换）
∵BE平分∠ABF（已知）
∴∠EBF=12______（____________）
∵FC平分∠BFG（已知）
∴∠CFB=12______（____________）
∴∠EBF＝______
∴BE∥CF（____________）
【变式6-3】（2022·内蒙古·扎赉特旗音德尔第三中学七年级期末）如图，点G在CD上，已知∠BAG+∠AGD=180°，EA平分∠BAG，FG平分∠AGC．请说明AE∥GF的理由．
解：因为∠BAG+∠AGD=180°(已知)，
∠AGC+∠AGD=180°(______)，
所以∠BAG=∠AGC(______)．
因为EA平分∠BAG，
所以∠1=12∠BAG(______)．
因为FG平分∠AGC，
所以∠2=12______，
得∠1=∠2(等量代换)，
所以______(______)．
【题型7 平行线判定的实际应用】
【例7】（2022·全国·七年级课时练习）如图，若将木条a绕点O旋转后使其与木条b平行，则旋转的最小角度为( )
A．65°B．85°C．95°D．115°
【变式7-1】（2022·河南·郑州外国语学校经开校区七年级阶段练习）如图所示的四种沿AB进行折叠的方法中，不一定能判断纸带两条边a，b互相平行的是（ ）
A．如图1，展开后测得∠1=∠2B．如图2，展开后测得∠1=∠2且∠3=∠4
C．如图3，测得∠1=∠2D．在图4中，展开后测得∠1+∠2=180°
【变式7-2】（2022·全国·七年级）一辆汽车在广阔的草原上行驶，两次拐弯后，行驶的方向与原来的方向相同，那么这两次拐弯的角度可能是（ ）
A．第一次向右拐40°，第二次向右拐140°．
B．第一次向右拐40°，第二次向左拐40°．
C．第一次向左拐40°，第二次向右拐140°．
D．第一次向右拐140°，第二次向左拐40°．
【变式7-3】（2022·江苏·南京外国语学校七年级期中）如图，a、b、c三根木棒钉在一起，∠1=70°,∠2=100°，现将木棒a、b同时顺时针旋转一周，速度分别为18度/秒和3度/秒，两根木棒都停止时运动结束，则___________秒后木棒a，b平行．