专题7.6 多边形及其内角和【十大题型】-最新苏教版七年级下册数学精讲精练

这是一份专题7.6 多边形及其内角和【十大题型】-最新苏教版七年级下册数学精讲精练，文件包含专题76多边形及其内角和十大题型-最新苏教版七年级下册数学精讲精练教师版docx、专题76多边形及其内角和十大题型-最新苏教版七年级下册数学精讲精练学生版docx等2份试卷配套教学资源，其中试卷共35页， 欢迎下载使用。
1、注重生活联系，形式活泼多样。初中生的数学思维能力正逐步由直观形象思维向抽象思维发展。这个发展需要一定的过程。
2、注重动手操作，引导学生“做”数学。有效的数学学习活动不能单纯地依赖模仿与记忆，自主探索与合作交流也是学习数学的重要方法。
3、注重“过程”和数学思想方法。新教材通过让学生亲身经历知识的形成过程，使学生的学习过程更多地成为其发现数学、了解数学、体验数学的过程。
专题7.6 多边形及其内角和【十大题型】
【苏科版】
TOC \ "1-3" \h \u
\l "_Tc21150" 【题型1 多边形及正多边形的概念辨析】 PAGEREF _Tc21150 \h 1
\l "_Tc28104" 【题型2 多边形的不稳定性】 PAGEREF _Tc28104 \h 2
\l "_Tc679" 【题型3 多边形的对角线】 PAGEREF _Tc679 \h 3
\l "_Tc933" 【题型4 多边形的内角和】 PAGEREF _Tc933 \h 4
\l "_Tc10702" 【题型5 多边形的外角和】 PAGEREF _Tc10702 \h 6
\l "_Tc17431" 【题型6 截角问题】 PAGEREF _Tc17431 \h 7
\l "_Tc30307" 【题型7 多边形内角和和外角和-平行线】 PAGEREF _Tc30307 \h 7
\l "_Tc9659" 【题型8 多边形内角和和外角和-角平分线】 PAGEREF _Tc9659 \h 8
\l "_Tc10223" 【题型9 多边形内角和和外角和的实际应用】 PAGEREF _Tc10223 \h 9
\l "_Tc1998" 【题型10 多边形内角和和外角和的的综合应用】 PAGEREF _Tc1998 \h 10
【知识点1 多边形的概念】
平面内，由一些线段 首尾顺次相接 所 组成的封闭图形，叫做多边形.
【知识点2 正多边形的概念】
各个角都相等,各条边都相等的多边形，叫做正多边形.
【题型1 多边形及正多边形的概念辨析】
【例1】（2022•秦都区校级月考）如图所示的图形中，属于多边形的有（ ）
A．3个B．4个C．5个D．6个
【变式1-1】（2022春•烟台期中）下列说法：①由许多条线段连接而成的图形叫做多边形；②多边形的边数是不小于4的自然数；③从一个多边形（边数为n）的同一个顶点出发，分别连接这个顶点与其余各顶点，可以把这个多边形分割成（n﹣2）个三角形；④半圆是扇形，其中正确的结论有（ ）
A．1个B．2个C．3个D．4个
【变式1-2】（2022•泸西县期末）下列图形：①等边三角形；②直角三角形；③平行四边形；④正方形，其中正多边形的个数有（ ）
A．1个B．2个C．3个D．4个
【变式1-3】（2022•肥西县期末）如图，下列图形是多边形的有 （填序号）．
【知识点3 多边形的不稳定性】
多边形具有不稳定性.
【题型2 多边形的不稳定性】
【例2】（2022•泸西县期末）如图的伸缩门，其原理是（ ）
A．三角形的稳定性B．四边形的不稳定性
C．两点之间线段最短D．两点确定一条直线
【变式2-1】（2022春•霞山区校级期末）下列图形中具有稳定性有（ ）
A．2个B．3个C．4个D．5个
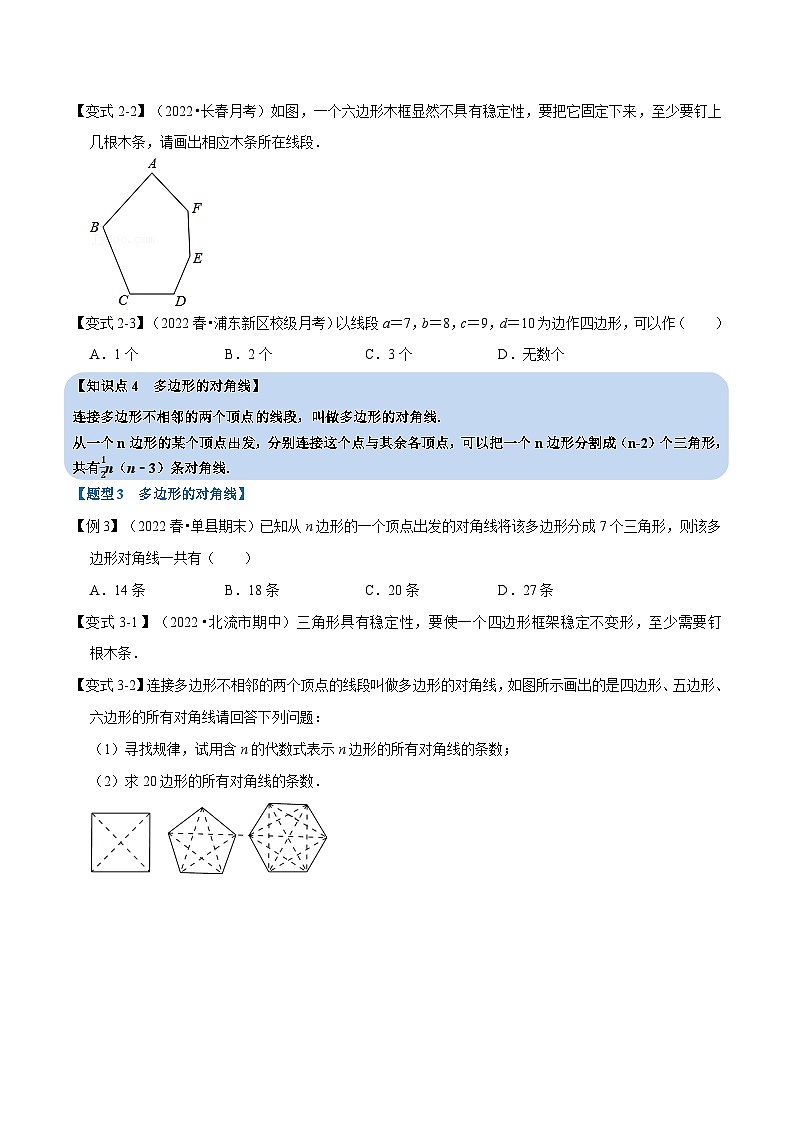
【变式2-2】（2022•长春月考）如图，一个六边形木框显然不具有稳定性，要把它固定下来，至少要钉上几根木条，请画出相应木条所在线段．
【变式2-3】（2022春•浦东新区校级月考）以线段a＝7，b＝8，c＝9，d＝10为边作四边形，可以作（ ）
A．1个B．2个C．3个D．无数个
【知识点4 多边形的对角线】
连接多边形不相邻的两个顶点的线段，叫做多边形的对角线.
从一个n边形的某个顶点出发，分别连接这个点与其余各顶点，可以把一个n边形分割成（n-2）个三角形，
共有12n（n﹣3）条对角线.
【题型3 多边形的对角线】
【例3】（2022春•单县期末）已知从n边形的一个顶点出发的对角线将该多边形分成7个三角形，则该多边形对角线一共有（ ）
A．14条B．18条C．20条D．27条
【变式3-1】（2022•北流市期中）三角形具有稳定性，要使一个四边形框架稳定不变形，至少需要钉 根木条．
【变式3-2】连接多边形不相邻的两个顶点的线段叫做多边形的对角线，如图所示画出的是四边形、五边形、六边形的所有对角线请回答下列问题：
（1）寻找规律，试用含n的代数式表示n边形的所有对角线的条数；
（2）求20边形的所有对角线的条数．
【变式3-3】（2021秋•长春月考）【教材重现】如图是数学教材第135页的部分截图．
在多边形中，三角形是最基本的图形．如图所示，每一个多边形都可以分割成若干个三角形．
数一数每个多边形中三角形的个数，你能发现什么规律？
在多边形中，连接不相邻的两个顶点，所得到的线段称为多边形的对角线．
【问题思考】结合如图思考，从多边形的一个顶点出发，可以得到的对角线的数量，并填写表：
【问题探究】n边形有n个顶点，每个顶点分别连接对角线后，每条对角线重复连接了一次，由此可推导出，n边形共有 条对角线（用含有n的代数式表示）．
【问题拓展】
（1）已知平面上4个点，任意三点不在同一直线上，一共可以连接 条线段．
（2）已知平面上共有15个点，任意三点不在同一直线上，一共可以连接 条线段．
（3）已知平面上共有x个点，任意三点不在同一直线上，一共可以连接 条线段（用含有x的代数式表示，不必化简）．
【知识点5 多边形的内角和】
n边形的内角和为(n-2)·180°(n≥3)．
【题型4 多边形的内角和】
【例4】（2022•孝感月考）如图，将六边形纸片ABCDEF沿虚线剪去一个角（∠BCD）后，得到∠1+∠2+∠3+∠4+∠5＝400°，求∠BGD的度数．
【变式4-1】（2022•梁园区校级期中）已知n边形的内角和θ＝（n﹣2）×180°．
（1）甲同学说，θ能取720°；而乙同学说，θ也能取820°，甲、乙的说法对吗？若对，求出边数n，若不对，说明理由；
（2）若n边形变为（n+x）边形，发现内角和增加了360°，用列方程的方法确定x．
【变式4-2】（2022•西平县期中）一个多边形，除一个内角外，其余各内角之和等于2012°，求这个内角的度数及多边形的边数．
【变式4-3】（2022春•宝应县校级月考）小马虎同学在计算某个多边形的内角和时得到1840°，老师说他算错了，于是小马虎认真地检查了一遍
（1）若他检查发现其中一个内角多算了一次，求这个多边形的边数是多少？
（2）若他检查发现漏算了一个内角，求漏算的那个内角是多少度？这个多边形是几边形？
【知识点6 多边形的外角和】
在一个多边形的每个顶点处各取一个外角，这些外角的和叫做多边形的外角和．n边形的外角和恒等于360°，它与边数的多少无关.
【题型5 多边形的外角和】
【例5】（2022•苍溪县月考）如图，∠1，∠2，∠3，∠4是五边形ABCDE的四个外角．若∠A＝120°，求∠1+∠2+∠3+∠4的度数．
【变式5-1】（2022•路北区期末）已知，正多边形的一个外角是30°，则这个正多边形是（ ）
A．六边形B．九边形C．十边形D．十二边形
【变式5-2】（2022•海口模拟）六边形的外角和为（ ）
A．360°B．540°C．720°D．1080°
【变式5-3】（2022•河北）如图，将三角形纸片剪掉一角得四边形，设△ABC与四边形BCDE的外角和的度数分别为α，β，则正确的是（ ）
A．α﹣β＝0B．α﹣β＜0
C．α﹣β＞0D．无法比较α与β的大小
【题型6 截角问题】
【例6】（2022•驿城区校级期末）若一个多边形截去一个角后变成了六边形，则原来多边形的边数可能是（ ）
A．5或6B．6或7C．5或6或7D．6或7或8
【变式6-1】（2022•安陆市期末）一个四边形剪去一个角后，它不可能是（ ）
A．三角形B．四边形C．五边形D．六边形
【变式6-2】（2022春•雨花区校级期末）把一个多边形纸片沿一条直线截下一个三角形后，变成一个18边形，则原多边形纸片的边数不可能是（ ）
A．16B．17C．18D．19
【变式6-3】（2022•怀柔区期末）如图是一个正方形，把此正方形沿虚线AB剪去一个角，得到一个五边形，则这个五边形的周长 原来正方形的周长．（填“大于”“小于”或“等于”），理由是 ．
【题型7 多边形内角和和外角和-平行线】
【例7】（2022春•侯马市期末）如图，六边形ABCDEF的内角都相等．
（1）若∠1＝60°，求∠ADC的度数；
（2）AB与ED有怎样的位置关系？为什么？
【变式7-1】（2022•平山县期末）嘉淇在折幸运星时将一张长方形的纸条折成了如图所示的样子（内部有一个正五边形），则∠1的度数为（ ）
A．36°B．54°C．60°D．72°
【变式7-2】（2022春•市中区期末）如图，在四边形ABCD中，∠A＝108°，∠C＝82°，M、N分别是AB、BC上的点，将△BMN沿着MN翻折，得到△EMN，若ME∥AD，EN∥DC，则∠E的度数为（ ）
A．88°B．87°C．86°D．85°
【变式7-3】（2022•临清市三模）如图，正五边形ABCDE，点D、E分别在直线m、n上．若m∥n，∠1＝20°，则∠2为（ ）
A．52°B．60°C．58°D．56°
【题型8 多边形内角和和外角和-角平分线】
【例8】（2022•藁城区二模）如图，六边形ABCDEF中，∠A，∠B，∠C，∠D的外角都相等，即∠1＝∠2＝∠3＝∠4＝62°，分别作∠DEF和∠EFA的平分线交于点P，则∠P的度数是（ ）
A．55°B．56°C．57°D．60°
【变式8-1】（2022•兴化市一模）如图，在四边形ABCD中，∠A＝150°，∠C＝60°，∠ABC与∠ADC的平分线交于点O，则∠BOD的度数为（ ）
A．120°B．125°C．130°D．135°
【变式8-2】（2022春•苏州月考）如图，在四边形ABCD中，∠A+∠B＝210°，作∠ADC、∠BCD的平分线交于点O1，再作∠O1DC、∠O1CD的平分线交于点O2，则∠O2的度数为 ．
【变式8-3】（2022春•惠民县期末）如图，CG平分正五边形ABCDE的外角∠DCF，并与∠EAB的平分线交于点O，则∠AOG的度数为（ ）
A．144°B．126°C．120°D．108°
【题型9 多边形内角和和外角和的实际应用】
【例9】（2022春•井研县期末）如图，大建从A点出发沿直线前进8米到达B点后向左旋转的角度为α，再沿直线前进8米，到达点C后，又向左旋转α角度，照这样走下去，第一次回到出发地点时，他共走了72米，则每次旋转的角度α为（ ）
A．30°B．40°C．45°D．60°
【变式9-1】（2022春•昌平区校级期中）科技馆为某机器人编制了一段程序，如果机器人在平地上按图所示的步骤行走，那么该机器人所走的总路程为（ ）
A．12米B．8米C．6米D．不能确定
【变式9-2】（2022•桓台县期末）如图，桐桐从A点出发，前进3m到点B处后向右转20°，再前进3m到点C处后又向右转20°，…，这样一直走下去，她第一次回到出发点A时，一共走了（ ）
A．100mB．90mC．54mD．60m
【变式9-3】（2022•株洲模拟）如图，若干相同正五边形排成环状．图中已经排好前3个五边形，还需 个五边形完成这一圆环．
【题型10 多边形内角和和外角和的的综合应用】
【例10】（2022春•临汾期末）在五边形ABCDE中，∠A，∠B，∠C，∠D，∠E的度数之比为3：5：3：4：3，则∠D的外角等于（ ）
A．60°B．75°C．90°D．120°
【变式10-1】（2022春•定陶县期末）请根据下面x与y的对话解答下列各小题：
x：我和y都是多边形，我们俩的内角和相加的结果为1440°；
y：x的边数与我的边数之比为1：3．
（1）求x与y的外角和相加的度数？
（2）分别求出x与y的边数？
（3）试求出y共有多少条对角线？
【变式10-2】（2022•富县月考）一个多边形的每个内角都相等，每个内角与相邻外角的差为100°，求这个多边形内角和的度数和边数．
【变式10-3】（2022•孝昌县期中）小明计算一个多边形的内角和时误把一个外角加进去了，得其和为2620°．
（1）求这个多加的外角的度数；
（2）求这个多边形的边数．多边形边数
四
五
六
…
十二
…
n
从一个顶点出发，得到对角线的数量
1条


…

…