高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用教案

这是一份高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用教案，共6页。
课例编号
2020QJ11SXRA014
学科
数学
年级
高二
学期
一
课题
空间向量的应用（2）
教科书
书名：
出版社： 出版日期： 年 月
教学人员
姓名
单位
授课教师
于洪伟
北京景山学校
指导教师
雷晓莉
东城区教师研修中心
教学目标
教学目标：运用空间向量研究立体几何中的度量问题的过程中，感受向量法和坐标法的区别和联系。
教学重点：运用空间向量研究例题几何中的度量问题。
教学难点：根据条件选择合适的思路和方法解题。
教学过程
时间
教学环节
主要师生活动
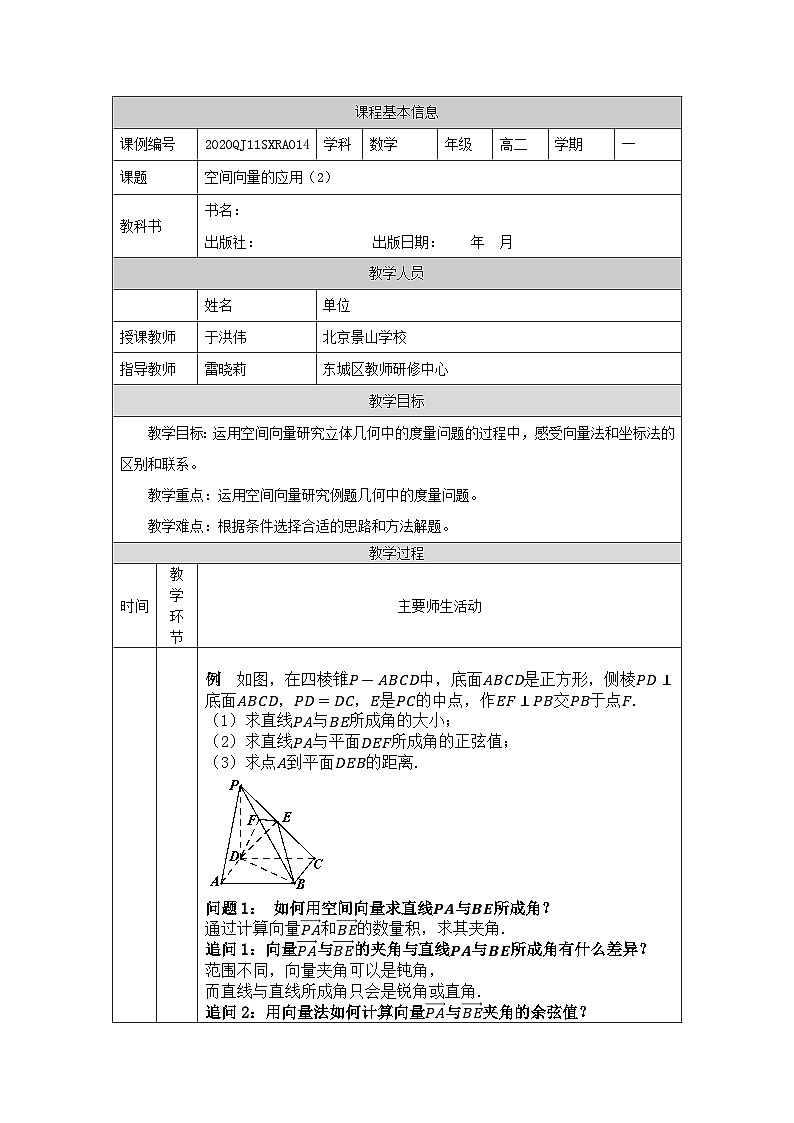
例 如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F.
（1）求直线PA与BE所成角的大小；
（2）求直线PA与平面DEF所成角的正弦值；
（3）求点A到平面DEB的距离.
问题1： 如何用空间向量求直线PA与BE所成角？
通过计算向量PA和BE的数量积，求其夹角.
追问1：向量PA与BE的夹角与直线PA与BE所成角有什么差异？
范围不同，向量夹角可以是钝角，
而直线与直线所成角只会是锐角或直角.
追问2：用向量法如何计算向量PA与BE夹角的余弦值？
PA=DA-DP，BE=-DA+12DP-DC.
（向量法）
解：因为PD⊥底面ABCD，所以PD⊥AD， PD⊥DC.
因为底面ABCD为正方形，所以AD⊥DC.
所以DA∙DP=0， DP∙DC=0，DA∙DC=0.
因为PA=DA-DP，BE=-DA+12DP-DC，
所以PA∙BE=(DA-DP)∙(-DA+12(DP-DC))
=-DA2+12DA∙DP-12DA∙DC+DP∙DA-12DP2+12DP∙DC
=-DA2-12DP2.
因为DA=DP=DC，所以DA2=DP2=DC2.
所以PA∙BE=-DA2-12DP2=-32DP2.
|PA|2=(DA-DP)2=DA2-2DA∙DP+DP2=DA2+DP2=2DP2，
|BE|2=(-DA+12(DP-DC))2
|BE|2=(-DA+12(DP-DC))2
=DA2+14DP2+14DC2-DA∙DP+DA∙DC+12DP∙DC=32DP2.
所以cs =PA∙BE|PA||BE|=-32DP22|DP|32|DP|=-32 .
所以向量PA，BE夹角为150°.
所以直线PA与BE夹角为30°.
追问3：如果用坐标法表示PA和BE，还用这个空间直角坐标系，能写出PA和BE的坐标么？
PA=1,0,-1，BE=(-1,-12,12).
（坐标法）解：因为PD⊥底面ABCD，所以PD⊥AD， PD⊥DC.
因为底面ABCD为正方形，所以AD⊥DC.
所以以D为原点，以DA为x轴，DC为y轴，DP为z轴，建立空间直角坐标系.设DA长为1.
可得D(0,0,0) ，A(1,0,0) B1,1,0，P0,0,1，E(0,12,12).
所以PA=1,0,-1，BE=(-1,-12,12).
所以cs =PA∙BE|PA||BE|
=1×-1+0×-12+(-1)×121+0+11+14+14=-32 .
所以向量PA，BE夹角为150°.
所以直线PA与BE夹角为30°.
问题3： 如何用向量法求直线PA与平面DEF所成角？
思路一是找到直线PA 在平面DEF 内的射影；
思路二是计算平面DEF 的法向量.
追问1： 你会倾向于采用哪条思路？
计算平面DEF 的法向量.
追问2： 向量PA与平面DEF法向量n的夹角和直线PA与平面DEF所成角θ是什么关系？
sinθ=|cs|
追问3：求平面DEF 的法向量需要解决什么问题？
直接找到与平面DEF垂直的向量；
或者找到平面DEF内不共线的两个向量.
（向量法）
解：采用（1）的基底向量，因为
PB=DA+DC-DP，DE=12DC+12DP，
所以PB∙DE=(DA+DC-DP)∙(12DC+12DP)
=12DC∙DA+12DP∙DA+12DC2+12DC∙DP-12DC∙DP-12DP2.
所以PB∙DE=12DC2-12DP2=0.
所以PB⊥DE.
因为EF⊥PB，所以EF⊥PB.
因为PB⊥DE， EF⊥PB，
所以PB是平面DEF的一个法向量.
因为 PB=DA+DC-DP，PA=DA-DP，
所以PA∙PB=2DP2，PA=2DP，|PB|=3DP.
所以cs =PA∙PB|PA||PB|=63.
所以PA与平面DEF所成角的正弦值等于63.
（坐标法）
解：采用（1）的空间直角坐标系，
所以PA=1,0,-1，PB=1,1,-1，DE=(0,12,12).
因为PB∙DE=1×0+0×12+-1×12=0，
所以PB⊥DE.
因为EF⊥PB，所以EF⊥PB.
所以PB是平面DEF的一个法向量.
因为cs =PA∙PBPAPB=1×1+0×1+-1×-11+0+11+1+1
=63，
所以PA与平面DEF所成角的正弦值等于63.
追问4：如果没有注意到PB是平面DEF的一个法向量，我们会需要计算点F的坐标来求平面DEF的一个法向量，怎样计算点F的坐标呢？
因为点F在PB上，所以PF=kPB.
而PB=1,1,-1，所以PF=k,k,-k.所以Fk,k,1-k.
所以 EF=(k,k-12,-k-12).
因为EF⊥PB，所以EF∙PB=0，
即k+k-12-(-k-12) =0.
解得 k=13，所以 F(13,13,23).
问题3：如何用空间向量求点A到平面DEB的距离？
计算向量DA 在平面DEB的法向量上的投影向量的长度.
追问1：还能直接找到平面DEB的法向量么？
找不到，只能通过找到平面DEB内不共线的
两个向量来计算平面DEB的法向量.
追问2：这时求平面DEB的法向量选择
向量法还是坐标法？
选择坐标法.
（3）解：仍采用（1）的空间直角坐标系，可得
DE=(0,12,12) ，DA=0,0, 1，DB=1,1, 0.
设平面DEB的法向量为m=(x,y,z)，
则有DE⋅m=0，DB⋅m=0. 即12y+12z=0，x+y=0.
令x=1，解得y=-1， z=1，所以m=(1,-1,1).
所以点A到平面DEB的距离为
DA∙mm=0×1+0×(-1)+1×11+1+1=33.
问题4：在研究立体几何中度量问题的过程中，对比一下，向量法和坐标法，有什么区别和联系？
联系：二者本质是相同的，坐标法实际上是向量法的坐标化，
区别：向量法并不要求基底向量互相垂直，只要两两数量积可求就可以了，坐标法依赖空间直角坐标系.
问题5：运用空间向量研究立体几何中度量问题的一般策略是什么？
课后练习
如图，在直三棱柱ABC-A1B1C1中，AA1=AC=2AB，且BC1⊥A1C.
（1）求平面ABC1与平面ABC夹角的大小；
（2）求点A1到直线BC1的距离.