初中数学鲁教版（五四学制）（2024）八年级下册1 菱形的性质与判定导学案

这是一份初中数学鲁教版（五四学制）（2024）八年级下册1 菱形的性质与判定导学案，共6页。学案主要包含了学习目标，知识梳理，典型例题，巩固训练等内容，欢迎下载使用。
【学习目标】
1.掌握菱形的面积公式；
2.会灵活运用菱形的有关知识进行计算和证明.
【知识梳理】
菱形的面积公式
如图，在菱形ABCD中，对角线AC、BD交于O点，若把菱形ABCD
看成△ABD和△BCD，而AO和OC分别是它们的高：
S菱形ABCD=S△ABD+S△BCD= + =BD× ，
即菱形的面积等于 乘积的 。（可以作为公式使用）
【典型例题】
知识点 菱形的面积
1.如图：四边形ABCD是边长为13cm的菱形，其中对角线BD长10cm.求:
（1）对角线AC的长度为多少cm.
（2）菱形ABCD的面积为多少cm2.
（1题图）

2．如图，四边形中，，平分，交于E．
(1)求证：四边形是菱形；
(2)在四边形中，与的度数比为，周长是．求四边形的面积．

（2题图）
【巩固训练】
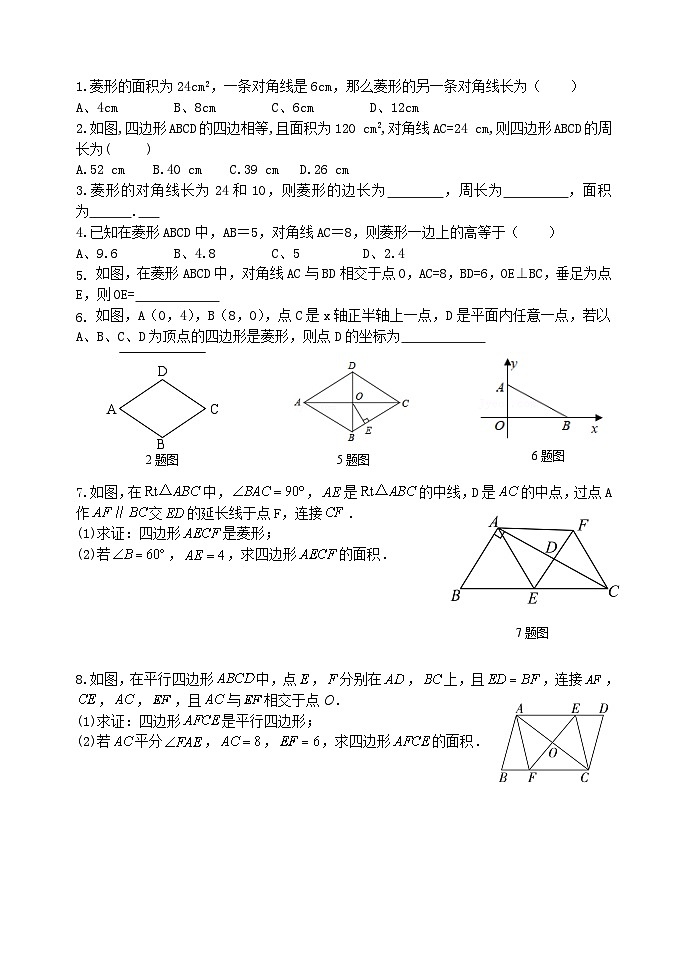
1.菱形的面积为24cm2，一条对角线是6cm，那么菱形的另一条对角线长为（ ）
A、4cm B、8cm C、6cm D、12cm
2.如图,四边形ABCD的四边相等,且面积为120 cm2,对角线AC=24 cm,则四边形ABCD的周长为( )
A.52 cm B.40 cm C.39 cmD.26 cm
3.菱形的对角线长为24和10，则菱形的边长为 ，周长为 ，面积为 .
4.已知在菱形ABCD中，AB＝5，对角线AC＝8，则菱形一边上的高等于（ ）
A、9.6 B、4.8 C、5 D、2.4
如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=8，BD=6，OE⊥BC，垂足为点E，则OE=
如图，A（0，4），B（8，0），点C是x轴正半轴上一点，D是平面内任意一点，若以A、B、C、D为顶点的四边形是菱形，则点D的坐标为
5题图
6题图
2题图
B
A
C
D
6题图
5题图
B
A
C
D
7.如图，在中，，是的中线，D是的中点，过点A作交的延长线于点F，连接．
(1)求证：四边形是菱形；
(2)若，，求四边形的面积．

7题图
8.如图，在平行四边形中，点，分别在，上，且，连接，，，，且与相交于点O．
(1)求证：四边形是平行四边形；
(2)若平分，，，求四边形的面积．
6.1 菱形的性质与判定（3）
【知识梳理】
1.1/2BD·AO 1/2BD·OC AC
2.两条对角线 一半
【典型例题】
解：（1）∵四边形ABCD是菱形
∴AC⊥BD ED=1/2BD AE=1/2AC
根据勾股定理
AE2=AD2=AE2
∴AE=12 AC=24cm
（2）S菱形ABCD=1/2AC·BD=1/2×24×10=120cm2
2. （1）证明：∵，
即，
又∵，
∴四边形是平行四边形，
∵平分，
∴，
又∵，
∴，
∴，
∴，
∴四边形是菱形；
（2）解：连接交于F点，
∵与的度数比为，且四边形是菱形，
所以，，
则是等边三角形，
又因为四边形周长是，
所以，
根据勾股定理得，，
四边形的面积为．
【巩固训练】
1.B 2.A 3.13 52 120
4.B 5.12/5 6.(5,4)或（4√5,4）
7. （1）证明：∵是的中线，，
∴，
∵D是的中点，
∴，
∵，
∴，
∴，
∴，
∴四边形是平行四边形，
又∵，
∴平行四边形是菱形；
（2）解：∵，，
∴，
∵四边形是菱形，
∴，，
∴，
∴，
∴，
∴．
8. 解：（1）解：证明：在平行四边形中，
．，
，
，
，
四边形是平行四边形；
（2），
，
，
，
，
四边形是平行四边形，
平行四边形是菱形，
∵，，
．