初中数学鲁教版（五四学制）（2024）八年级下册2 矩形的性质与判定学案设计

这是一份初中数学鲁教版（五四学制）（2024）八年级下册2 矩形的性质与判定学案设计，共4页。学案主要包含了学习目标，知识梳理，典型例题，巩固训练，巩固练习等内容，欢迎下载使用。
【学习目标】
1.理解并掌握矩形的判定方法；
2.会用矩形的判定定理进行有关的论证或计算.
【知识梳理】
1.定义法： 叫做矩形.
2.矩形相对于一般平行四边形来讲，特殊在“对角线”和“角”上.
我们可以从“对角线”和“角”两方面得到矩形的判定定理：
矩形的判定定理（1）：________________________________________________________
矩形的判定定理（2）：________________________________________________________
3.独立证明矩形的判定定理（1），（2）.
（1）对角线相等的平行四边形是矩形.
已知： 求证：
证明
A
B
C
D
（2）有三个角是直角的四边形是矩形.
已知： 求证：
证明
【典型例题】
知识点一 对角线相等的平行四边形是矩形.
1题图
1.如果，是斜边上的中线，延长到点，使，连接、．四边形是矩形吗？请说明理由．
1题图
知识点二 有三个角是直角的四边形是矩形.
2.如图,在▱ABCD中,AE⊥BC,CF⊥AD,E,F分别为垂足.求证:四边形AECF是矩形.
2题图
2题图
【巩固训练】
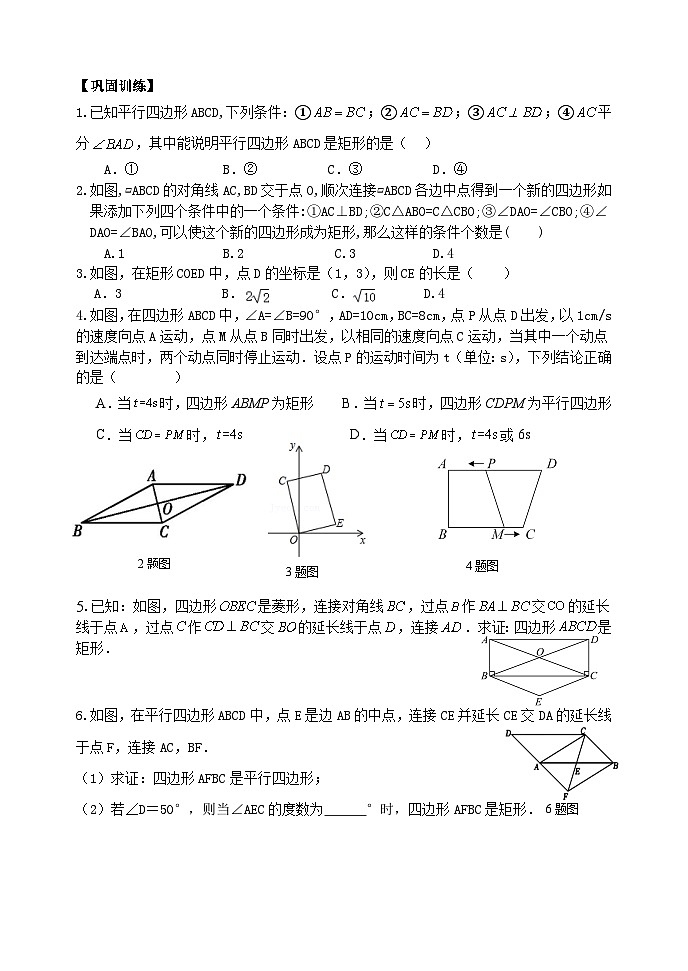
1.已知平行四边形ABCD,下列条件：①；②；③；④平分，其中能说明平行四边形ABCD是矩形的是（ ）
A．① B．② C．③ D．④
2.如图,▱ABCD的对角线AC,BD交于点O,顺次连接▱ABCD各边中点得到一个新的四边形,如果添加下列四个条件中的一个条件:①AC⊥BD;②C△ABO=C△CBO;③∠DAO=∠CBO;④∠DAO=∠BAO,可以使这个新的四边形成为矩形,那么这样的条件个数是( )
A.1 B.2 C.3 D.4
3.如图，在矩形COED中，点D的坐标是（1，3），则CE的长是（ ）
A．3B． C． D.4
4题图
3题图
4.如图，在四边形ABCD中，∠A=∠B=90°，AD=10cm，BC=8cm，点P从点D出发，以1cm/s的速度向点A运动，点M从点B同时出发，以相同的速度向点C运动，当其中一个动点到达端点时，两个动点同时停止运动．设点P的运动时间为t（单位：s），下列结论正确的是（ ）
A．当时，四边形ABMP为矩形 B．当时，四边形CDPM为平行四边形
3题图
C．当时， D．当时，或6s
2题图
2题图
4题图
5.已知：如图，四边形是菱形，连接对角线，过点作交的延长线于点，过点作交的延长线于点，连接．求证：四边形是矩形．
6题图
6.如图，在平行四边形ABCD中，点E是边AB的中点，连接CE并延长CE交DA的延长线于点F，连接AC，BF．
（1）求证：四边形AFBC是平行四边形；
（2）若∠D＝50°，则当∠AEC的度数为 °时，四边形AFBC是矩形．
6.2矩形的性质与判断（2）
【知识梳理】
1.有一个角是直角的平行四边形
2.对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
【巩固练习】
1.B 2.C 3.C 4.D
5. 解：（证明：四边形为菱形，
∴，
∴，
∵，，
，，
在和中，
，
，
，
∴四边形为平⾏四边形，
，
∴为矩形．
6（1）证明：∵四边形ABCD是平行四边形，
∴DA∥CB，
∴∠EAF＝∠EBC，
∵点E是边AB的中点，
∴AE＝BE，
在△AEF和△BEC中，
∠EAF＝∠ECB
AE＝BE
∠AEF＝∠BEC，
∴△AEF≌△BEC（ASA），
∴EF＝EC，
又∵AE＝BE，
∴四边形AFBC是平行四边形；
（2）解：当∠AEC的度数为100度时，四边形AFBC是矩形，
理由：∵四边形AFBC是矩形，
∴AB＝CF，
∴EC＝EB，
∴∠ECB＝∠EBC，
∵四边形ABCD是平行四边形，∠D＝50°，
∴∠D＝∠EBC＝50°，
∴∠ECB＝50°，
∴∠AEC＝∠ECB＋∠EBC＝50°＋50°＝100°，
故答案为：100．