2024-2025学年广东省肇庆市德庆县、四会市高三上学期12月联考数学检测试题（附解析）

这是一份2024-2025学年广东省肇庆市德庆县、四会市高三上学期12月联考数学检测试题（附解析），共15页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
一、单选题（本大题共8小题）
1．设集合，集合，则等于（ ）
A．B．
C．D．
2．已知圆锥的底面半径为，其侧面展开图为一个半圆，则该圆锥的母线长为（ ）
A．B．C．D．
3．在中，点D在边AB上，．记，则（ ）
A．B．C．D．
4．已知函数是定义域为的偶函数，在区间上单调递增，且对任意，均有成立，则下列函数中符合条件的是（ ）
A．B．C．D．
5．已知圆柱的高为2，侧面积为，若该圆柱的上、下底面圆周都在某一球的球面上，则该球的体积为（ ）
A．B．C．D．
6．已知是各项均为正数的等差数列，且，则的最大值为（ ）
A．10B．20C．25D．50
7．已知，则（ ）
A．B．C．D．
8．已知是定义在R上的奇函数，当时，，若函数是偶函数，则下列结论不正确的为（ ）
A．B．的最小正周期
C．有4个零点D．
二、多选题（本大题共3小题）
9．设 为复数， .下列命题中正确的是（ ）
A．若，则
B．若，则
C．若，则
D．若，则
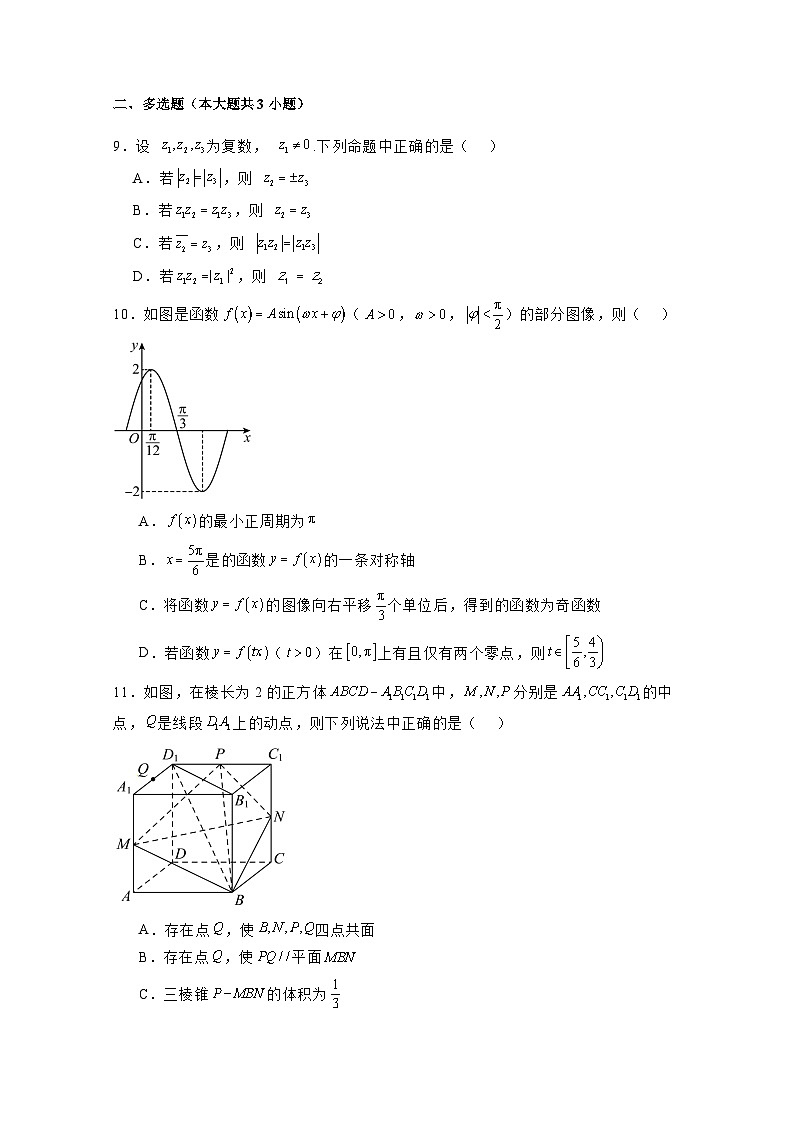
10．如图是函数（，，）的部分图像，则（ ）

A．的最小正周期为
B．是的函数的一条对称轴
C．将函数的图像向右平移个单位后，得到的函数为奇函数
D．若函数（）在上有且仅有两个零点，则
11．如图，在棱长为2的正方体中，分别是的中点，是线段上的动点，则下列说法中正确的是（ ）
A．存在点，使四点共面
B．存在点，使平面
C．三棱锥的体积为
D．经过四点的球的表面积为
三、填空题（本大题共3小题）
12．记Sn为等比数列{an}的前n项和.若，则S4= ．
13．曲线在处的切线的倾斜角为，则的值为
14．已知若函数有两个零点，则的取值范围为
四、解答题（本大题共5小题）
15．在中，角A，B，C的对边分别是a，b，c，满足．
(1)求B；
(2)已知点D在边AC上，且BD是的平分线，，求的最小值．
16．如图，在三棱柱ABC﹣A1B1C1中，侧面ABB1A1是菱形，且CA＝CB1．
（1）证明：面CBA1⊥面CB1A；
（2）若∠BAA1＝60°，A1C＝BC＝BA1，求二面角C﹣A1B1﹣C1的余弦值．
17．已知函数.
(1)求的极值；
(2)对任意，不等式恒成立，求的取值范围.
18．设数列的前项和为，已知.
(1)证明：数列是等比数列；
(2)若数列满足，，求数列的前项的和．
19．记分别为函数的导函数．若存在，满足且，则称为函数与的一个“点”．
（1）证明：函数与不存在“点”；
（2）若函数与存在“点”，求实数的值；
（3）已知函数，．对任意a>0，判断是否存在，使函数与在区间内存在“点”，并说明理由．
答案
1．【正确答案】A
【分析】解不等式求得集合，根据并集定义运算得解.
【详解】,
,
∴=.
故选A.
2．【正确答案】B
【分析】设圆锥的母线长为，根据圆锥底面圆的周长等于扇形的弧长可求得的值，即为所求.
【详解】设圆锥的母线长为，由于圆锥底面圆的周长等于扇形的弧长，则，解得.
故选B.
3．【正确答案】B
【分析】根据几何条件以及平面向量的线性运算即可解出．
【详解】因为点D在边AB上，，所以，即，
所以．
故选B．
4．【正确答案】B
【详解】对于A：定义域为，
且，不符合题意，故A错误；
对于B：因为定义域为，且，
即函数是定义域为的偶函数，当时，，则在上单调递增，
又，符合题意，故B正确.
对于C：因为为奇函数，不符合题意，故C错误；
对于D：，则，不符合题意，故D错误；
故选：B
5．【正确答案】A
【详解】由圆柱侧面积，解得，
因为圆柱的上、下底面圆周都在某一球的球面上，
所以球心在圆柱高的中点处，设球半径为，
则由，
所以,
故选：A
6．【正确答案】C
【详解】∵，∴，
由已知，得，
∴，当且仅当时等号成立.
故选：C.
7．【正确答案】C
【分析】先根据已知结合两角和差的正弦公式及二倍角公式化简，求出，再根据两角差的正切公式即可得解.
【详解】由，
得，
即，所以，
所以，
所以.
故选C.
8．【正确答案】D
【详解】对于A：由题意可得：，解得，故A正确；
对于B：∵是偶函数，则，则，
又∵为奇函数，则，可得，
∴，则的最小正周期，故B正确；
对C：令，则，
注意到此时，分别作出的图象，
由图象可知：有4个交点，故有4个零点，
故C正确；
对D：∵，
则，
可得，故D不正确.
故选：D.
9．【正确答案】BC
【详解】A：由复数模的概念可知，不能得到，例如，，A错误；
B：由可得，因为，所以，即，B正确；
C：若，则，有，
则，故，故C正确；
D：取，，显然满足，但，D错误.
故选：BC．
10．【正确答案】AD
【详解】由图像可知， ， ，即，故A正确；
，此时，
又 在图像上， ，解得，
，
，， ，
当是函数的一条对称轴时，此时不符合题意，故B错误；
将的图象向右平移个单位后得到的图象对应的解析式为：
不为奇函数，故C错误；
令 ，解得 ，
当 时， ，不合题意
时， ；时， ；时， ；
又因为函数在上有且仅有两个零点
，解得 ，故D正确.
故选：AD.
11．【正确答案】ABC
【详解】A：如图，在正方体中，连接．
因为N，P分别是的中点，所以．
又因为，所以．
所以四点共面，即当Q与点重合时，四点共面，故A正确；
B：连接，当Q是的中点时，因为，所以．
因为平面平面，所以平面，故B正确；
C：连接，因为，则
，故C正确；
D：分别取的中点E，F，构造长方体，
则经过C，M，B，N四点的球即为长方体的外接球．
设所求外接球的直径为，则长方体的体对角线即为所求的球的直径，
即，
所以经过C，M，B，N四点的球的表面积为，故D错误．
故选：ABC
12．【正确答案】.
【详解】详解：设等比数列的公比为，由已知
，即
解得，
所以．
13．【正确答案】
【详解】根据已知条件，，因为曲线在处的切线的倾斜角为，所以，.因为，，则解得，，故.
故
14．【正确答案】
【详解】当时，，则，
所以当时，f′x>0，函数单调递增；
当时，f′x0，函数单调递增；当时，f′x0恒成立，此时单调递增，无极值；
当时，令，得.
故当时，单调递减；
当时，单调递增，
此时在处取到极小值，无极大值.
（2）方法一：对任意时，恒成立，即恒成立.
令，则.
令，则，
即ℎx在区间0,1上单调递减，又，
所以当时，ℎx>0，即，此时单调递增；
当时，ℎx0，设．
因为，且h（x）的图象是不间断的，
所以存在∈（0，1），使得，令，则b>0．
函数，
则．
由f（x）与g（x）且f′（x）与g′（x），得
，即（**）
此时，满足方程组（**），即是函数f（x）与g（x）在区间（0，1）内的一个“S点”．
因此，对任意a>0，存在b>0，使函数f（x）与g（x）在区间（0，+∞）内存在“S点”．
点睛：涉及函数的零点问题、方程解的个数问题、函数图象交点个数问题，一般先通过导数研究函数的单调性、最大值、最小值、变化趋势等，再借助函数的大致图象判断零点、方程根、交点的情况，归根到底还是研究函数的性质，如单调性、极值，然后通过数形结合的思想找到解题的思路.