2025高考数学【真题精编】基础精选——函数与导数

这是一份2025高考数学【真题精编】基础精选——函数与导数，文件包含06函数与导数70题教师版docx、06函数与导数70题学生版docx等2份试卷配套教学资源，其中试卷共60页， 欢迎下载使用。
一、单选题
1．（2008·海南）已知，若，则等于（ ）
A．B．C．D．
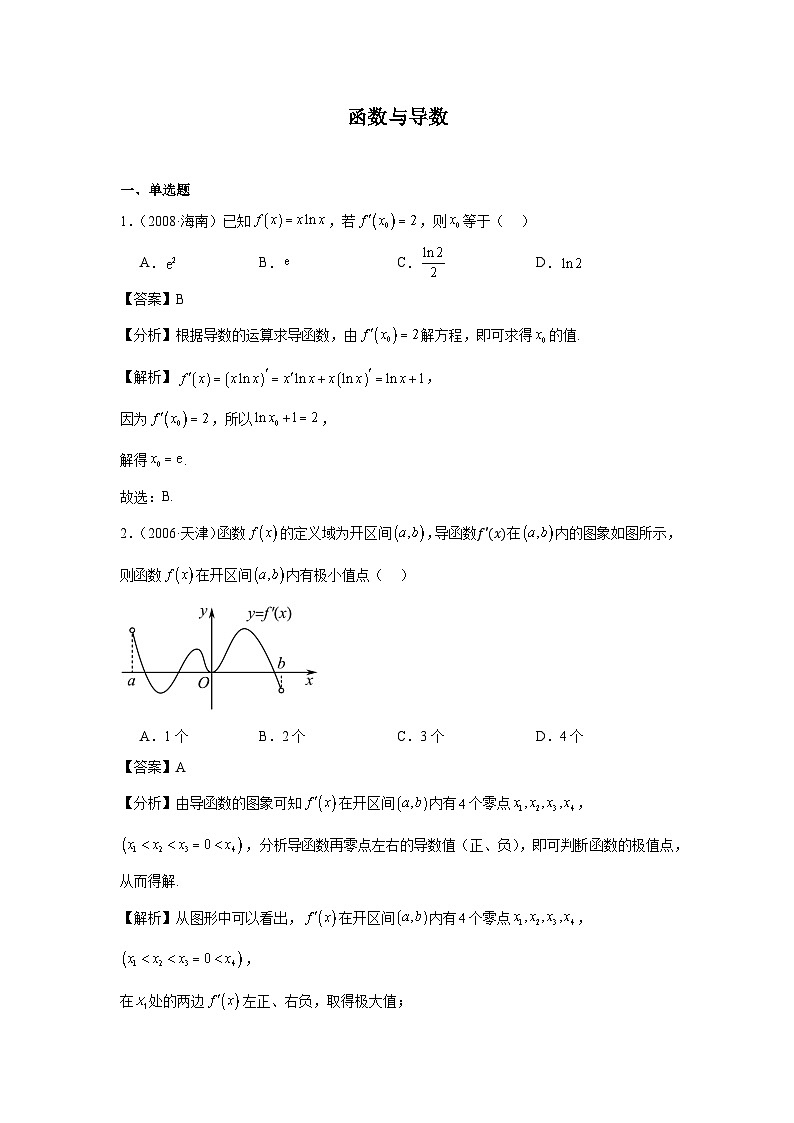
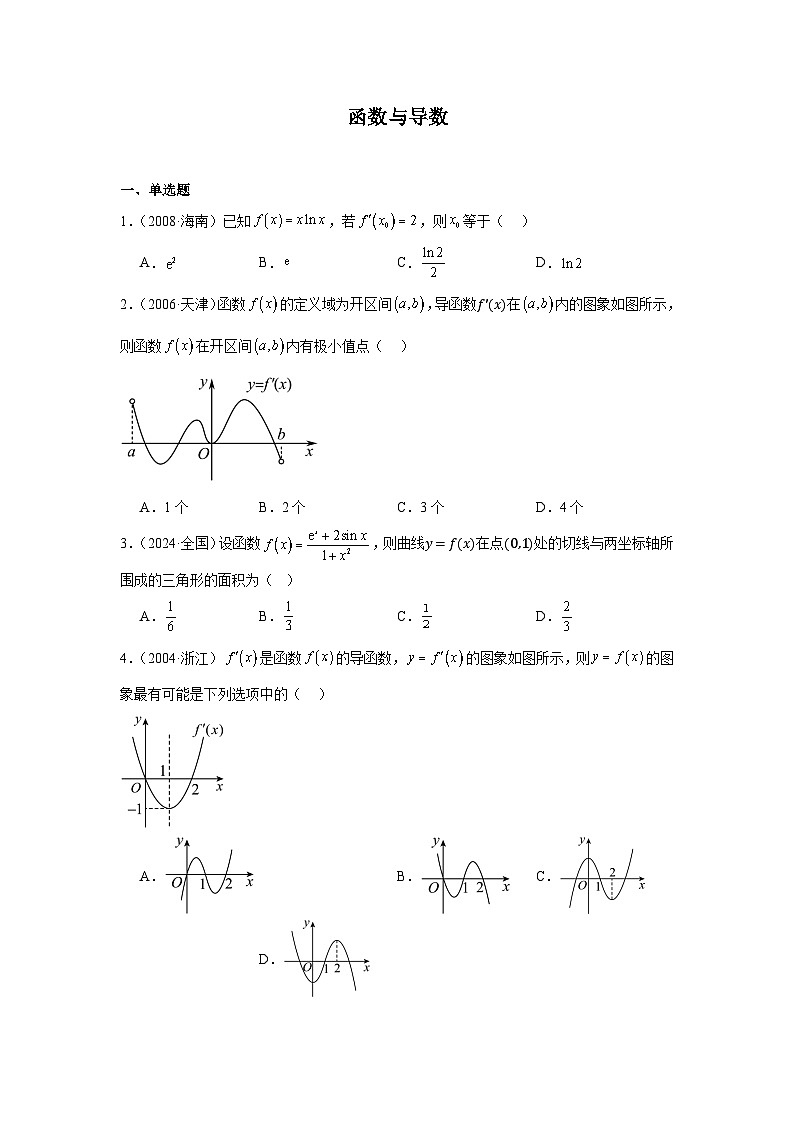
2．（2006·天津）函数的定义域为开区间，导函数f′x在内的图象如图所示，则函数在开区间内有极小值点（ ）
A．1个B．2个C．3个D．4个
3．（2024·全国）设函数，则曲线y=fx在点0,1处的切线与两坐标轴所围成的三角形的面积为（ ）
A．B．C．D．
4．（2004·浙江）是函数的导函数，的图象如图所示，则的图象最有可能是下列选项中的（ ）

A． B． C． D．
5．（2023·北京）已知数列满足，则（ ）
A．当时，为递减数列，且存在常数，使得恒成立
B．当时，为递增数列，且存在常数，使得恒成立
C．当时，为递减数列，且存在常数，使得恒成立
D．当时，为递增数列，且存在常数，使得恒成立
6．（2023·全国）函数存在3个零点，则的取值范围是（ ）
A．B．C．D．
7．（2023·全国）曲线在点处的切线方程为（ ）
A．B．C．D．
8．（2023·全国）已知函数在区间上单调递增，则a的最小值为（ ）．
A．B．eC．D．
9．（2022·全国）当时，函数取得最大值，则（ ）
A．B．C．D．1
10．（2007·全国）已知曲线y＝－3ln x的一条切线的斜率为，则切点的横坐标为（ ）
A．3B．2C．1D．
11．（2021·全国）设，若为函数的极大值点，则（ ）
A．B．C．D．
12．（2021·全国）若过点可以作曲线的两条切线，则（ ）
A．B．
C．D．
13．（2008·全国）曲线在点处的切线的倾斜角为（ ）
A．30°B．45°C．60°D．135°
14．（2020·全国）若直线l与曲线y=和x2+y2=都相切，则l的方程为（ ）
A．y=2x+1B．y=2x+C．y=x+1D．y=x+
15．（2020·全国）函数的图像在点处的切线方程为（ ）
A．B．
C．D．
16．（2019·全国）已知曲线在点处的切线方程为，则
A．B．C．D．
17．（2019·天津）已知，设函数若关于的不等式在上恒成立，则的取值范围为
A．B．C．D．
18．（2019·全国）曲线y=2sinx+csx在点(π，–1)处的切线方程为
A．B．
C．D．
19．（2012·天津）函数在区间(0,1)内的零点个数是
A．0B．1C．2D．3
20．（2013·辽宁）设函数满足则时，
A．有极大值，无极小值B．有极小值，无极大值
C．既有极大值又有极小值D．既无极大值也无极小值
21．（2012·湖南）设定义在R上的函数是最小正周期为2π的偶函数，是的导函数，当时，；当且时 ，，则函数在上的零点个数为（ ）
A．2B．4C．5D．8
22．（2012·陕西）设函数f（x）=+lnx ，则 （ ）
A．x=为f(x)的极大值点B．x=为f(x)的极小值点
C．x=2为 f(x)的极大值点D．x=2为 f(x)的极小值点
23．（2014·全国）已知函数，若存在唯一的零点，且，则的取值范围是
A．B．C．D．
24．（2018·全国）设函数．若为奇函数，则曲线在点处的切线方程为( )
A．B．C．D．
25．（2017·全国）已知函数有唯一零点，则
A．B．C．D．1
26．（2017·全国）若是函数的极值点，则的极小值为．
A．B．C．D．
27．（2016·全国）若函数在上单调递增，则的取值范围是
A．B．C．D．
28．（2015·全国）设函数是奇函数（）的导函数，，当时，，则使得成立的的取值范围是
A．B．(−1,0)∪(1,+∞)
C．D．
29．（2014·全国）若函数在区间上单调递增，则实数的取值范围是
A．B．C．2,+∞D．
30．（2014·辽宁）当时，不等式恒成立，则实数a的取值范围是
A．B．C．D．
31．（2013·福建）设函数的定义域为R，是的极大值点，以下结论 一定正确的是
A．B．是的极小值点
C．是的极小值点D．是的极小值点
32．（2004·湖北）函数有极值的充要条件是
A．B．C．D．
33．（2009·安徽）已知函数在R上满足，则曲线在
点处的切线方程是
A．B．C．D．
二、多选题
34．（2024·广东江苏）设函数，则（ ）
A．是的极小值点B．当时，
C．当时，D．当时，
35．（2023·全国）已知函数的定义域为，，则（ ）．
A．B．
C．是偶函数D．为的极小值点
36．（2023·全国）若函数既有极大值也有极小值，则（ ）．
A．B．C．D．
37．（2022·全国）已知函数，则（ ）
A．有两个极值点B．有三个零点
C．点是曲线的对称中心D．直线是曲线的切线
三、填空题
38．（2024·全国）曲线与在上有两个不同的交点，则的取值范围为 ．
39．（2024·广东江苏）若曲线在点处的切线也是曲线的切线，则 .
40．（2023·全国）设，若函数在上单调递增，则a的取值范围是 .
41．（2022·全国）若曲线有两条过坐标原点的切线，则a的取值范围是 ．
42．（2021·全国）写出一个同时具有下列性质①②③的函数 ．
①；②当时，；③是奇函数．
43．（2007·湖北）已知函数的图像在点处的切线方程是，则＝ ．
44．（2020·全国）设函数．若，则a= ．
45．（2018·全国）已知函数，则的最小值是 ．
46．（2018·天津）已知函数f(x)=exlnx，为f(x)的导函数，则的值为 ．
47．（2017·江苏）已知函数，其中e是自然数对数的底数，若，则实数a的取值范围是 ．
48．（2017·天津）已知，设函数的图象在点（1，）处的切线为l，则l在y轴上的截距为 .
49．（2016·全国）已知为偶函数，当时，，则曲线在点处的切线方程是 ．
50．（2016·全国）若直线是曲线的切线，也是曲线的切线，则 ．
51．（2015·全国）已知函数的图像在点的处的切线过点，则 .
52．（2015·天津）已知函数，其中为实数，为的导函数，若，则的值为 ．
53．（2015·陕西）设曲线在点（0,1）处的切线与曲线上点处的切线垂直，则的坐标为 ．
54．（2015·安徽）设，其中均为实数，下列条件中，使得该三次方程仅有一个实根的是 .（写出所有正确条件的编号）
①；②；③；④；⑤.
55．（2014·全国）若函数在区间内是减函数，则实数的取值范围是 .
56．（2014·江苏）在平面直角坐标系中，若曲线（为常数）过点，且该曲线在点处的切线与直线平行，则 .
57．（2010·天津）设函数，对任意，恒成立，则实数的取值范围是 .
四、解答题
58．（2007·全国）已知函数．
（1）求曲线在点处的切线方程；
（2）设，如果过点可作曲线的三条切线，证明：
59．（2012·北京）已知函数，（），
（1）若曲线与曲线在它们的交点（1，c）处具有公共切线，求a,b的值
（2）当时，若函数在区间[k,2]上的最大值为28，求k的取值范围
60．（2012·重庆）设函数，其中在，曲线在点处的切线垂直于轴
（Ⅰ）求a的值；
（Ⅱ）求函数极值．
61．（2007·天津）已知函数，其中．
(1)当时，求曲线在点处的切线方程；
(2)当时，求函数的单调区间与极值．
62．（2006·安徽）设函数f（x）=x3+bx2+cx（x∈R），已知g（x）=f（x）﹣f′（x）是奇函数
（1）求b、c的值．
（2）求g（x）的单调区间与极值．
63．（2016·全国）设函数，其中α＞0，记 的最大值为A．
（Ⅰ）求；
（Ⅱ）求A；
（Ⅲ）证明.
64．（2013·福建）已知函数当时，求曲线在点处的切线方程；求函数的极值
65．（2012·重庆）已知函数在处取得极值.
（1）求a、b的值；
（2）若有极大值28，求在上的最小值.
66．（2012·福建）已知函数f（x）=ex＋ax2-ex，a∈R[
（Ⅰ）若曲线y=f（x）在点（1，f（1））处的切线平行于x轴，求函数f（x）的单调区间；
（Ⅱ）试确定a的取值范围，使得曲线y=f（x）上存在唯一的点P，曲线在该点处的切线与曲线只有一个公共点P
67．（2004·全国）已知直线l1为曲线y＝x2+x﹣2在点（1，0）处的切线，l2为该曲线的另一条切线，且l1⊥l2．
（Ⅰ）求直线l2的方程；
（Ⅱ）求由直线l1、l2和x轴所围成的三角形的面积．
68．（2010·江西）设函数.
（1）若的两个极值点为，且，求实数的值；
（2）是否存在实数，使得是上的单调函数？若存在,求出的值；若不存在，说明理由.
69．（2010·全国）已知函数．
（Ⅰ）设，求的单调区间；
（Ⅱ）设在区间中至少有一个极值点，求a的取值范围．
70．（2008·浙江）已知是实数，函数.
（Ⅰ）若，求的值及曲线在点处的切线方程；
（Ⅱ）求在区间[0，2]上的最大值．