

所属成套资源:2024-2025北京各区九上数学期末试卷与答案
2-西城 2024-2025第一学期初三数学期末试卷答案
展开
这是一份2-西城 2024-2025第一学期初三数学期末试卷答案,共6页。试卷主要包含了176π.,. 14, 解,5°,,证明等内容,欢迎下载使用。
一、选择题(共16分,每题2分)
二、填空题(共16分,每题2分)
9.(3,). 10.65°. 11.答案不唯一,如. 12.176π.
13.. 14.. 15. (4,0),(,). 16.②④.
三、解答题(共68分,第17题5分,第18题6分,第19-21每题5分,第22题6分,第23题5分,第24题6分,第25题5分,第26题6分,第27-28题每题7分)
解答应写出文字说明、演算步骤或证明过程.
17.解:,,.1分
>0.2分
方程有两个不相等的实数根
4分
.
方程的根为,.5分
18. 解:(1)补全图形,如图所示; 3分
(2)90,直径所对的圆周角是直角,经过半径的外端并
且垂直于这条半径的直线是圆的切线.6分
19. 解:(1)
;2分
(2)图象如图所示;4分
(3)1<x<3.5分
20. (1)解:∵ 将△DCB绕点C旋转得到△ECA,
∴ △DCB≌△ECA.
∴ ∠DBC=∠EAC.
∵ ∠CDB=∠FDA,
∴ ∠ACB=∠AFB.
∵ ∠ACB=90°,
∴ ∠AFB=90°.
∴ ∠BFE=90°.2分
(2)证明:∵ △ECA≌△DCB,
∴ ∠ACE=∠ACB=90°,
∠AEC=∠BDC.
∵ ∠BDC=67.5°,
∴ ∠AEC=67.5°.
∴ ∠EAC=22.5°.
∵ △ACB中,∠ACB=,AC=BC,
∴ ∠BAC=45°.
∴ ∠BAE=∠AEB=67.5°.
∴ AB=EB.
∵ ∠BFE=90°,
∴ BF⊥AE.
∴ AF=EF.5分
21.(1)证明:Δ1分
.
因为≥0,
所以Δ≥0.
所以方程总有两个实数根. 2分
(2)解:解方程,得,3分
整理,得或.
∵ 方程的一个根比另一个根大3,
∴ 或.4分
∴ 或.5分
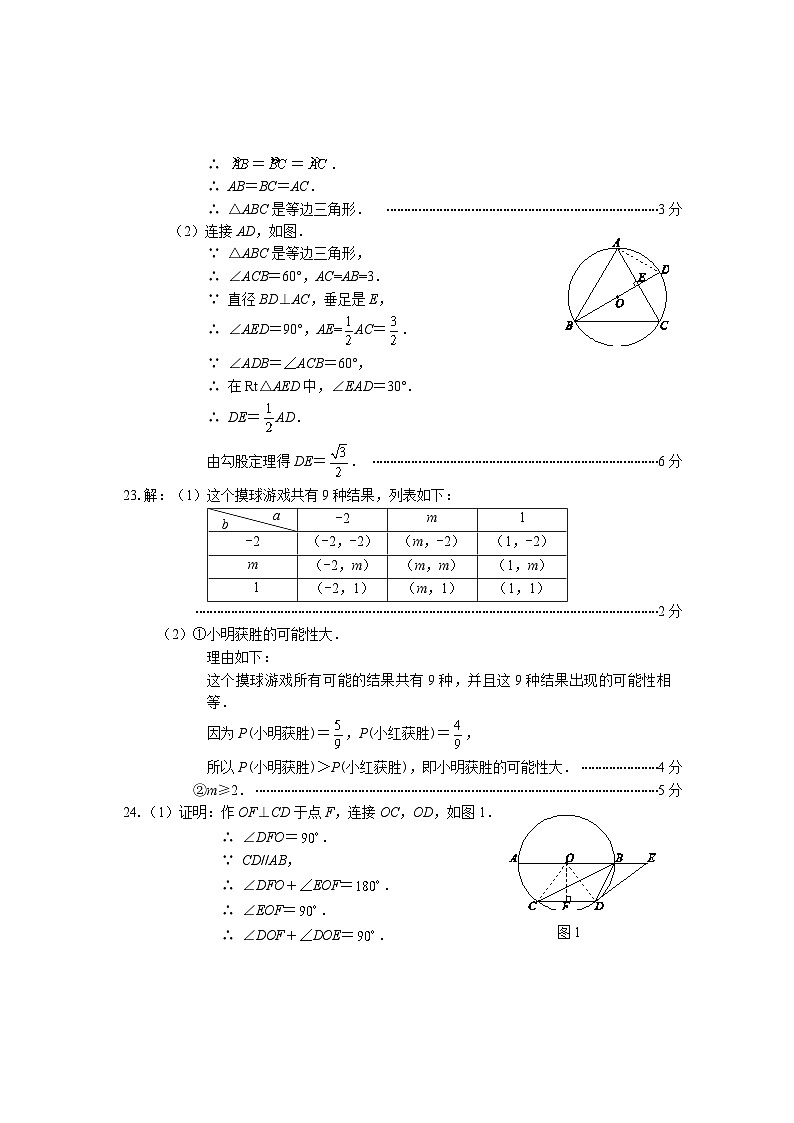
22. 解:(1)∵ 直径BD⊥AC,垂足是E,
∴ =.
∵ =,
∴ ==.
∴ AB=BC=AC.
∴ △ABC是等边三角形. 3分
(2)连接AD,如图.
∵ △ABC是等边三角形,
∴ ∠ACB=60°,AC=AB=3.
∵ 直径BD⊥AC,垂足是E,
∴ ∠AED=90°,AE=AC=.
∵ ∠ADB=∠ACB=60°,
∴ 在Rt△AED中,∠EAD=30°.
∴ DE=AD.
由勾股定理得DE=. 6分
a
23.解:(1)这个摸球游戏共有9种结果,列表如下:
2分
(2)①小明获胜的可能性大.
理由如下:
这个摸球游戏所有可能的结果共有9种,并且这9种结果出现的可能性相等.
因为P(小明获胜)=,P(小红获胜)=,
所以P(小明获胜)>P(小红获胜),即小明获胜的可能性大.4分
②m≥2.5分
图1
24.(1)证明:作OF⊥CD于点F,连接OC,OD,如图1.
∴ ∠DFO=.
∵ CD//AB,
∴ ∠DFO+∠EOF=.
∴ ∠EOF=.
∴ ∠DOF+∠DOE=.
∵ DE是⊙O的切线,D是切点,
∴ OD⊥DE.
∴ ∠ODE=.
∴ ∠E+∠DOE=.
∴ ∠E=∠DOF.
∵ OC=OD,
∴ ∠DOF=
∵ ∠CBD=,
∴ ∠DOF=∠CBD.
∴ ∠E=∠CBD.3分
(2)解:作DG⊥AE于点G,如图2.
∵ CD//AB,OF⊥CD于点F,
∴ DG⊥CD,OF⊥AE.
∴ DG=OF.
设⊙O的半径为r,则OA=OD=r.
∵ AE=8,
∴ OE=8- r. 图2
∵ 在Rt△ODE中,∠ODE=90°,DE=4,
∴ .
解得r=3.
∴ OE=5.
∴ OF=DG==.
∴ 在Rt△DFO中,DF==.
∴ CD=2DF=.6分
25.解:(1)由已知得所求的函数关系:.
∵ 点(0,0)在函数的图象上,
∴ 16a+16=0.
∴ a=-1.
∴ 所求的函数关系:.2分
(2)①这位患者存在中毒风险,理由如下:
由条件可得第一次和第二次服药间隔的时间是3小时,则该患者的血药总浓度y与时间x的函数关系:
(3≤x≤8).
整理后,得.
所以y的最大值为27.5.
由于27.5>24,
所以这位患者存在中毒风险.4分
②4<t≤7.5分
26.解:抛物线(a≠0)的对称轴为x=a.
(1)∵ =,
∴ 点A,B关于直线x=a对称.
∴ =.
∵ m=-1,
∴ a=.2分
(2)∵ a>0,
∴ -a<0.
①当x<a时,y随着x的增大而减小,
∵ 当时,都有,
∴ ≤-a.
∴ n+1≤-1.
∴ n≤-2.4分
②当x≥a时,y随着x的增大而增大,
点A关于直线x=a的对称点的坐标是.
∵ 当时,都有,
∴ na≥3a.
∴ n≥3.
综上,n的取值范围是n≤-2或n≥3.6分
图1
27.(1)①补全图形,如图1所示;1分
②线段PC,BF,AE之间的数量关系:AE=PC+BF.
证明:连接PB,如图2.
∵ 线段DB绕点D逆时针旋转得到线段DP,
∴ DB = DP,∠BDP = 60°.
∴ △DPB是等边三角形.2分
∴ BD = BP,∠DBP = 60°.
∵ △ABC是等边三角形,
∴ AB = BC,∠ABC = 60°.
∴ ∠ABC =∠DBP.
∴ =.
∴ =.
∴ △ABD≌△CBP.3分
∴ AD=PC.
∵ PF⊥BD于H,
∴ ∠BHF=∠BHP=90°.
设∠ABD=α,则∠BFP=90°-α.
∵ ∠ABC=∠ACB=60°,∠DBE=30°,
∴ ∠ABD+∠CBE=30°.
∴ ∠CBE=30°-α.
图2
∴ ∠BED=∠ACB+∠CBE=90°-α.
∴ ∠BFP =∠BED.
∵ ∠DBP=60°,
∴ ∠BPF=30°.
∴ ∠BPF=∠DBE.
∴ △BPF≌△DBE.5分
∴ BF=DE.
∴ AE = AD + DE = PC + BF.6分
(2)7分
28.解:(1)①3;1分
②5≤t≤9;3分
(2)≤k≤或k≥.7分
题号
1
2
3
4
5
6
7
8
答案
A
B
A
D
D
C
C
B
b
-2
m
1
-2
(-2,-2)
(m,-2)
(1,-2)
m
(-2,m)
(m,m)
(1,m)
1
(-2,1)
(m,1)
(1,1)
相关试卷
这是一份13-平谷 2024-2025第一学期初三数学期末试卷答案,共6页。
这是一份11-昌平 2024-2025第一学期初三数学期末试卷答案,共6页。试卷主要包含了 解,证明,补全图形略等内容,欢迎下载使用。
这是一份9-通州 2024-2025第一学期初三数学期末试卷答案,共10页。试卷主要包含了选择题,填空题,解答题解答应写出文字说明等内容,欢迎下载使用。









