初中数学人教版（2024）七年级下册（2024）7.1.2 两条直线垂直集体备课课件ppt

这是一份初中数学人教版（2024）七年级下册（2024）7.1.2 两条直线垂直集体备课课件ppt，共34页。PPT课件主要包含了学习目标，课堂小结，当堂小练，新课导入，拓展与延伸，知识回顾，对接中考，邻补角互补，对顶角相等，对顶角等内容，欢迎下载使用。
4. 知识点1垂线的概念
5. 知识点2垂线的画法及性质
1. 理解垂线的概念.2. 会用三角尺或量角器过一点画已知直线的垂线.3. 体会作已知直线的垂线的存在性和唯一性，归纳出垂线的基本事实.
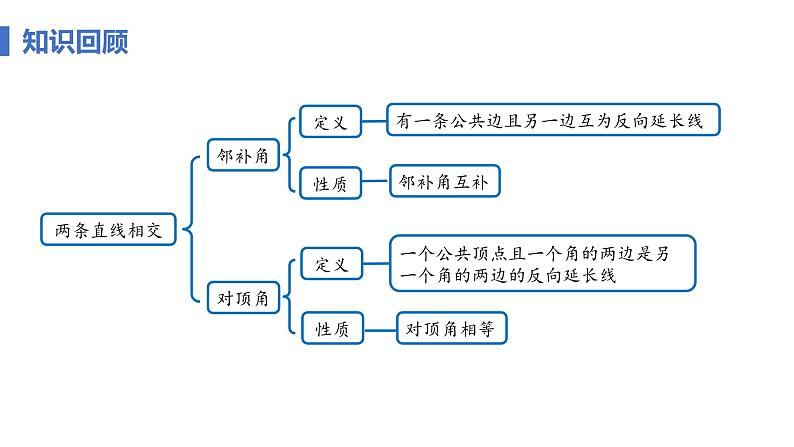
有一条公共边且另一边互为反向延长线
一个公共顶点且一个角的两边是另一个角的两边的反向延长线
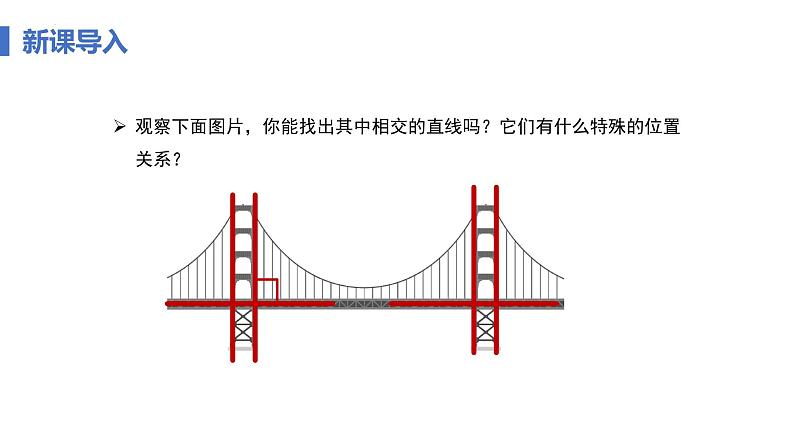
观察下面图片，你能找出其中相交的直线吗？它们有什么特殊的位置关系？
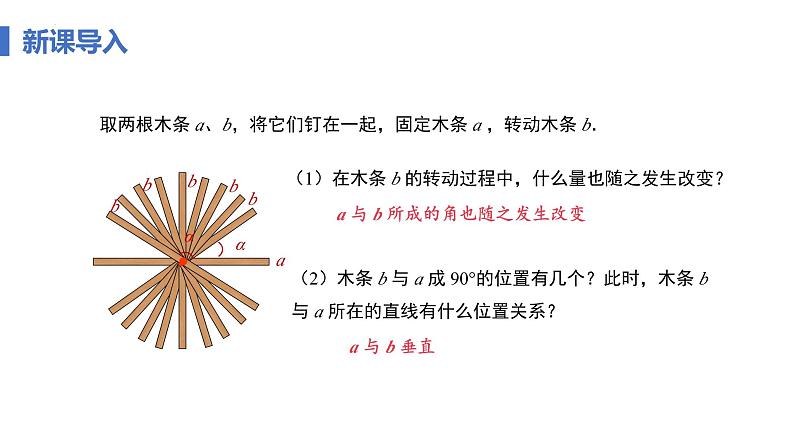
取两根木条 a、b，将它们钉在一起，固定木条 a ，转动木条 b．
（1）在木条 b 的转动过程中，什么量也随之发生改变？
a 与 b 所成的角也随之发生改变
（2）木条 b 与 a 成 90°的位置有几个？此时，木条 b 与 a 所在的直线有什么位置关系？
知识点1 垂线的概念
在相交线的模型中，固定木条a，转动木条b. 当b的位置变化时，a，b所成的角∠α也会发生变化.
当∠α=90°时，我们说a与b互相垂直，记作a⊥b.
当两条直线相交所形成的四个角中，有一个角是直角时，就称这两条直线互相垂直. 其中一条直线叫作另一条直线的垂线；它们的交点叫作垂足.
如右图，直线AB与直线CD垂直，记作：AB⊥CD，垂足是O；  
“⊥”是“垂直”的记号，读作“垂直于”；而“┐”是图形中“垂直”(直角)的标记.
如图，直线 AB 与 CD 相交于点 O，若∠BOC = 90°，则AB，CD 互相垂直，记作“AB⊥CD”，读作“AB 垂直于 CD”，直线 AB 叫做直线 CD 的垂线(或直线 CD 叫做直线 AB 的垂线)，交点 O 叫做垂足.
如果用 l，m 表示这两条直线，那么直线 l 与直线 m 垂直，可记作：l⊥m (或 m⊥l ).
可以写成下面的形式：因为∠AOD=90°，(已知)所以AB⊥CD. (垂直的定义)
反过来，如果AB⊥ CD，那么∠AOD是多少度？写出这个推理过程
如果AB⊥CD，(已知)那么∠AOD=90°. (垂直的定义)
注意：两条直线互相垂直是它们相交的一种特殊情况.
垂直的定义具有双重作用：①知线垂直得直角；②知直角得线垂直.
如图，①若 AB⊥CD，则∠BOC =∠AOC =∠AOD =∠BOD =90°； ②若∠BOC =90°，则 AB⊥CD.
【问题】1. 两条直线垂直和相交是什么关系？
2. 能否认为在同一平面内，两条直线的位置关系有 3 种：相交，平行，垂直？
不能，因为垂直是相交的特殊情况
3. 如何判定两条射线垂直？两条线段呢？
两条线段垂直、两条射线垂直、线段与射线垂直、线段与直线垂直、射线与直线垂直，都是指它们所在的直线垂直．
1. 如图，AO⊥CO，直线 BD 经过点 O，且∠1 =20°，则∠COD 的度数为( )A.70°B.110°C.140°D.160°
∠COB =90°-20°=70°
∠COD =180°- 70°= 110°
当两条直线相交所成的四个角都相等时，这两条直线有什么位置关系？为什么？
解：当两条直线相交所成的四个角都相等时，这两条直线的位置关系是互相垂直.这是因为当两条直线相交时，它们所形成的四个角总和为360°.如果每个角都相等，那么每个角的度数即为90°，也就是直角.因此，这两条直线是垂直的‌.
知识点2 垂线的画法及性质
1. 画已知直线l的垂线能画几条？2. 过直线 l 上的一点A画l的垂线，这样的垂线能画几条？3. 过直线 l 外的一点B画l的垂线，这样的垂线能画几条？
【问题】这样画 l 的垂线可以画几条？
【探究】用三角尺或量角器画已知直线l的垂线.（1）如图，已知直线 l，画 l 的垂线.
【探究】用三角尺或量角器画已知直线l的垂线.（2）经过直线l上一点A画l的垂线，这样的垂线能画出几条？
“一落”“二移”“三画”
让三角尺的一条直角边落在已知直线上，使其与已知直线重合
沿已知直线移动三角尺，使其另一条直角边经过已知点·
沿此直角边画直线，则这条直线就是已知直线的垂线，
【探究】用三角尺或量角器画已知直线l的垂线.(3)经过直线l外一点B画l的垂线，这样的垂线能画出几条？
可以发现，经过一点（在已知直线上或直线外），能画出已知直线的一条垂线，并且只能画出一条垂线.
垂线的基本事实：在同一平面内，过一点有且只有一条直线与已知直线垂直.
1. 不能忽略“在同一平面内”这个条件，因为如果不在同一平面内，那么过一点有无数条直线与已知直线垂直.2.“有且只有”指“存在且唯一”.
2. 如图，过点P画出射线AB或线段AB的垂线.
画一条线段或射线的垂线，就是画它们所在直线的垂线，垂足可能在这条线段或射线上，也可能在线段的延长线上或射线的反向延长线上.
1. 如图，分别过点P作线段MN的垂线.
2. 下列说法正确的有（ ）：①两条直线相交，交点叫做垂足；②在同一平面内，过一点有且只有一条直线与已知直线垂直；③在同一平面内，一条直线有且只有一条垂线；④在同一平面内，一条线段有无数条垂线；⑤过一点不可能向一条射线或线段作垂线；⑥若l1⊥l2，则l1是 l2的垂线，l2不是 l1的垂线. A.2个B.3个C.4个D.5个
在同一平面内，过一点有且只有一条直线与已知直线垂直.
当两条直线相交所成的四个角中有一个角为 90°时，这两条直线互相垂直， 其中一条直线叫做另一条直线的垂线.
利用三角尺或量角器画：一靠、二过、三画
1. 如图所示，若 AB ⊥ CD 于点 O ，则∠AOD = _____；若∠BOD = 90°，则 AB _____ CD.
2. 如图，在三角形ABC中，过点B画边AC的垂线，下列画法正确的是 ( )
垂足有时在线段的延长线或射线的反向延长线上，所画的垂线是实线.若需延长线段或反向延长射线，则用虚线。
3. 在下列条件中：①两直线相交所成的四个角都是直角；②两直线相交，对顶角互补；③两直线相交所成的四个角都相等，可以判定两条直线互相垂直的是（ ）A.①②B.①③C.②③D.①②③
4. 在直线AB 上任取一点O，过点O作射线OC，OD，使OC⊥OD 于点O.当∠AOC=30°时，∠BOD的度数为( )
A.60°B.120°C.60°或90°D.60°或120°
解：分两种情况讨论：①如图①，因为OC⊥OD，所以∠COD=90°,所以∠BOD=180°-∠AOC-∠COD=60°;②如图②，因为OC⊥OD，所以∠COD=90°,所以∠AOD=∠COD-∠AOC=60°,所以∠BOD=180°-∠AOD=120°.综上所述，∠BOD的度数为60°或120°.
5. 如图，直线 AB 和 CD 交于点 O，OD 平分∠BOF，OE⊥CD，垂足为 O，若∠AOC = 40°，则 ∠EOF =_______.
∠EOF = 90°+∠DOF
∠AOC = ∠DOB
∠EOF = 90°+40° = 130°
6. 如图，AB ⊥ l ，BC ⊥ l ，B 为垂足，那么 A、B、C 三点在同一直线上吗？为什么？
解：A、B、C 三点在同一直线上.∵AB ⊥ l ，BC ⊥ l . 且交点都为 B .∴A、B、C 三点在同一直线上（在同一平面内，过一点有且只有一条直线与已知直线垂直）.
7. 如图，已知O为直线AB上一 点，OE平分∠BOC，OD平分∠AOC，则OE与OD有什么位置关系?为什么?
∠2+∠AOC = 90°
∠BOC = ∠1+90°
∠MOD = 180°-∠1
需求出 ∠1 的度数
设∠1 = x°，列方程 x+2x=90求∠1
∠MOD = 150°
∠BOC = 120°
与已知角度建立联系 (可设未知数列方程）
如图，直线AB，CD相交于点O，EO⊥ CD，垂足为O，若∠ 1=54°，则∠ 2 的度数为( )A. 26° B. 36°C. 44° D.54°
1. 如图，直线 AB，CD 相交于 O 点，OM⊥AB 于 O .（1）若∠1 =∠2，求∠NOD；（2）若∠BOC = 4∠1，求∠AOC 与∠MOD.
解：（1）∵ OM ⊥ AB ，∴∠1 + ∠AOC = 90°.又∵∠1 = ∠2，∴∠2 + ∠AOC = 90°，∴∠NOD = 180°-（∠2 + ∠AOC）= 180°- 90°= 90°.
（2）由已知条件∠BOC = 4∠1，即 90°+∠1 = 4∠1，可得∠1 = 30°，∴∠AOC = 90°- 30° = 60°，∴由对顶角相等可得∠BOD = 60°，∴∠MOD = 90°+∠BOD = 150°.