2025高考数学二轮复习-专题1 函数与导数 第5讲 利用导数研究函数的零点【课件】

这是一份2025高考数学二轮复习-专题1 函数与导数 第5讲 利用导数研究函数的零点【课件】，共44页。PPT课件主要包含了基础回扣•考教衔接，以题梳点•核心突破，目录索引等内容，欢迎下载使用。
1.(人B选必三6.2节习题)已知函数f(x)=x3-x2-x-1的图象与直线y=c有3个不同的交点,求实数c的取值范围.
2.(人A选必二第五章例题)给定函数f(x)=(x+1)ex.(1)判断函数f(x)的单调性,并求出f(x)的极值;(2)画出函数f(x)的大致图象;(3)求出方程f(x)=a(a∈R)的解的个数.
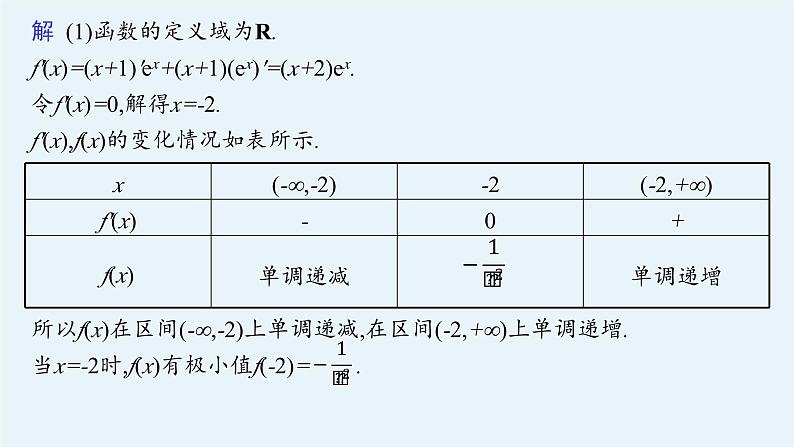
解 (1)函数的定义域为R.f'(x)=(x+1)'ex+(x+1)(ex)'=(x+2)ex.令f'(x)=0,解得x=-2.f'(x),f(x)的变化情况如表所示.
所以f(x)在区间(-∞,-2)上单调递减,在区间(-2,+∞)上单调递增.当x=-2时,f(x)有极小值f(-2)= .
(2)令f(x)=0,解得x=-1.当x0.
1.(2023·全国乙,文8)若函数f(x)=x3+ax+2存在3个零点,则a的取值范围是(　　)A.(-∞,-2)　　　　　　B.(-∞,-3)C.(-4,-1) D.(-3,0)
(方法二)令f(x)=0,得-ax=x3+2,易知x≠0,所以-a=设g(x)= ,则函数f(x)存在3个零点等价于函数g(x)= 的图象与直线y=-a有三个不同的交点.g'(x)= .当x>1时,g'(x)>0,函数g(x)在(1,+∞)内单调递增,当x0,函数h(x)单调递增;当x∈(0,2)时,h'(x)0,函数t(x)单调递增.
画出函数h(x)的图象如图所示.
考点三 隐零点问题*
例3(2024·江西赣州一模)已知函数f(x)=ex-1-ln x.(1)求f(x)的单调区间;(2)已知m>0,若函数g(x)=f(x)-m(x-1)有唯一的零点x0.求证:10,f(x)单调递增.∴f(x)的减区间为(0,1),增区间为(1,+∞).
[对点训练3](2024·山东淄博一模)已知函数f(x)=ex-sin x-1.(1)讨论函数f(x)在区间(0,+∞)上的单调性;(2)证明:函数f(x)在区间(-π,0]上有且仅有两个零点.(1)解 函数f(x)=ex-sin x-1,当x>0时,f'(x)=ex-cs x>1-cs x>0,所以f(x)在(0,+∞)上单调递增.