




所属成套资源:2025高考数学二轮复习专辑-【课件】
2025高考数学二轮复习-专题突破练6 平面向量【课件】
展开
这是一份2025高考数学二轮复习-专题突破练6 平面向量【课件】,共28页。PPT课件主要包含了ABD等内容,欢迎下载使用。
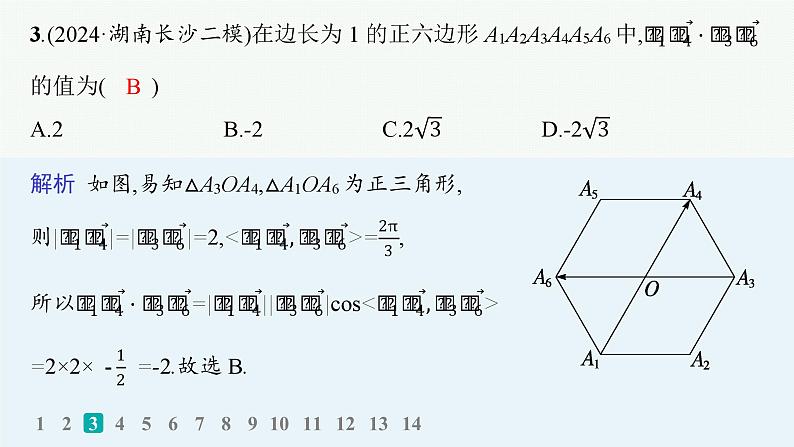
1.(2024·河北承德二模)在△ABC中,D为BC中点,连接AD,设E为AD中点,且
A.4x+2yB.-4x+yC.-4x-2yD.4y-2x
2.(2024·江苏南京二模)已知向量a=(1,2),b=(x,x+3).若a∥b,则x=( )A.-6B.-2C.3D.6解析 由a∥b,知1·(x+3)=2·x,解得x=3.故选C.
4.(2024·浙江绍兴二模)已知e1,e2是单位向量,且它们的夹角是60°,若a=2e1+e2,b=λe1-e2,且a⊥b,则λ=( )
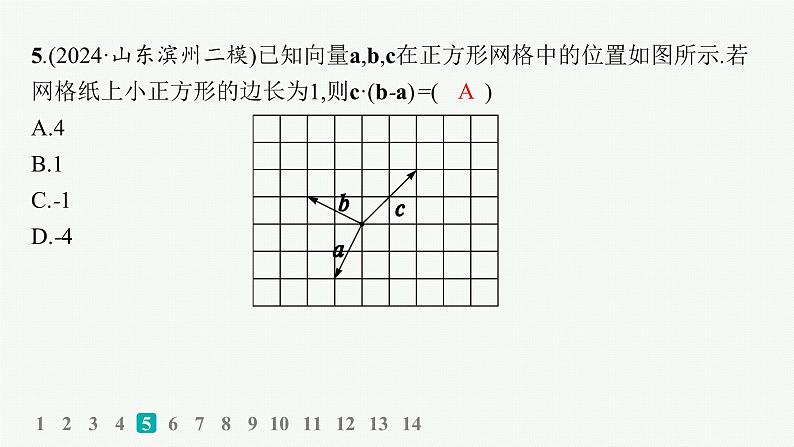
5.(2024·山东滨州二模)已知向量a,b,c在正方形网格中的位置如图所示.若网格纸上小正方形的边长为1,则c·(b-a)=( )
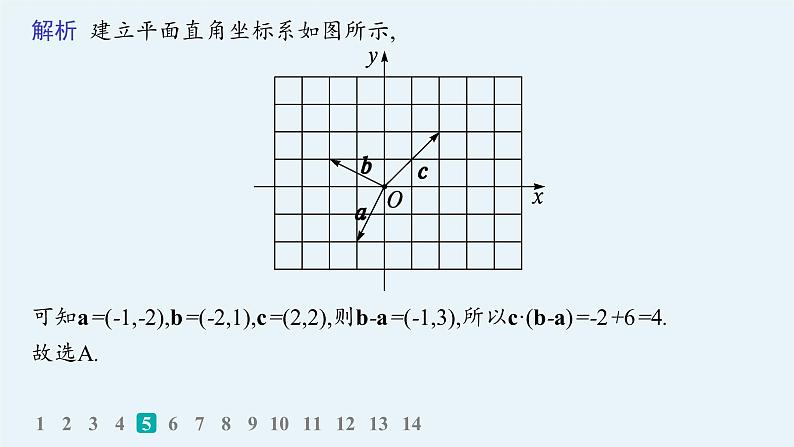
解析 建立平面直角坐标系如图所示,
可知a=(-1,-2),b=(-2,1),c=(2,2),则b-a=(-1,3),所以c·(b-a)=-2+6=4.故选A.
9.(2024·浙江温州模拟预测)已知单位向量a,b,c共面,则下列说法中正确的是( )A.若|a+b|=|a-b|,则a∥bB.若|a+b|=|a-b|,则a⊥b
解析 由|a+b|=|a-b|,可得(a+b)2=(a-b)2,即a2+b2+2a·b=a2+b2-2a·b,可得a·b=0,所以a⊥b,故A不正确,B正确.因为向量a,b,c为单位向量,可得|a|=|b|=|c|=1.又a+b+c=0,可得b=-(a+c),则b2=a2+c2+2a·c,即|b|2=|a|2+|c|2+2a·c,
10.(2024·山东济宁模拟)如图2,这是一个边长为20厘米的正六边形的软木锅垫ABCDEF,则下列选项正确的是( )
解析 以A为原点,以AB所在直线为x轴,AE所在直线为y轴,建立平面直角坐标系,如图所示.
11.(2024·山东潍坊三模)已知向量a=(1,2),b=(4,-2),c=(1,λ),若c·(2a+b)=0,则实数λ= . 解析 2a+b=(2,4)+(4,-2)=(6,2),c·(2a+b)=(1,λ)·(6,2)=6+2λ=0,解得λ=-3.
解析如图,以B为原点,以BC,BA所在的直线为x轴、y轴,建立平面直角坐标系,
14.(15分)(2024·湖南长沙一模)“费马点”是由数学家费马提出,该问题是:“在一个三角形内求作一点,使其与此三角形的三个顶点的距离之和最小.”意大利数学家托里拆利给出了解答,当△ABC的三个内角均小于120°时,使得∠AOB=∠BOC=∠COA=120°的点O即为费马点;当△ABC有一个内角大于或等于120°时,最大内角的顶点为费马点.试用以上知识解决下面问题:已知△ABC的内角A,B,C所对的边分别为a,b,c,且cs 2B+cs 2C-cs 2A=1.(1)求A;(2)若bc=2,设点P为△ABC的费马点,求
解 (1)由cs 2B+cs 2C-cs 2A=1,得1-2sin2B+1-2sin2C-1+2sin2A=1,故sin2A=sin2B+sin2C.由正弦定理可得a2=b2+c2,故△ABC是直角三角形,且A= .
相关课件
这是一份2025高考数学二轮复习-专题突破练20 直线与圆【课件】,共23页。
这是一份2025高考数学二轮复习-专题突破练11 数列的递推关系【课件】,共28页。
这是一份2025高考数学二轮复习-专题突破练4 利用导数研究不等式【课件】,共16页。









