浙江省吴兴高级中学2024-2025学年高二上学期10月阶段性测试数学试卷（Word版附解析）

这是一份浙江省吴兴高级中学2024-2025学年高二上学期10月阶段性测试数学试卷（Word版附解析），文件包含浙江省吴兴高级中学2024-2025学年高二上学期10月阶段性测试数学试题Word版含解析docx、浙江省吴兴高级中学2024-2025学年高二上学期10月阶段性测试数学试题Word版无答案docx等2份试卷配套教学资源，其中试卷共23页， 欢迎下载使用。
1. 直线的倾斜角为（ ）
A. 150°B. 120°C. 60°D. 30°
【答案】D
【解析】
【分析】由斜率得倾斜角．
【详解】直线的斜率为，所以倾斜角为30°.
故选：D．
2. 已知向量，，则向量在向量上的投影向量为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】根据投影向量的计算公式计算即可.
【详解】向量在向量上的投影向量为，
故选：C.
3. 已知点，，若直线过点且与线段相交，则直线的斜率的取值范围是（ ）
A. 或B. 或
C. 或D.
【答案】D
【解析】
【分析】根据两点间斜率公式计算即可.
【详解】直线的斜率为，直线的斜率为，
结合图象可得直线的斜率的取值范围是.
故选：D
4. 四棱锥中，，，，则该四棱锥的高为（ ）
A. 1B. 2C. 3D. 4
【答案】A
【解析】
【分析】先求出平面的法向量，再根据点到面的距离的向量公式求解即可.
【详解】设平面的法向量为，
则有，令，则，
所以，
所以点P到平面的距离即该四棱锥的高为.
故选：A.
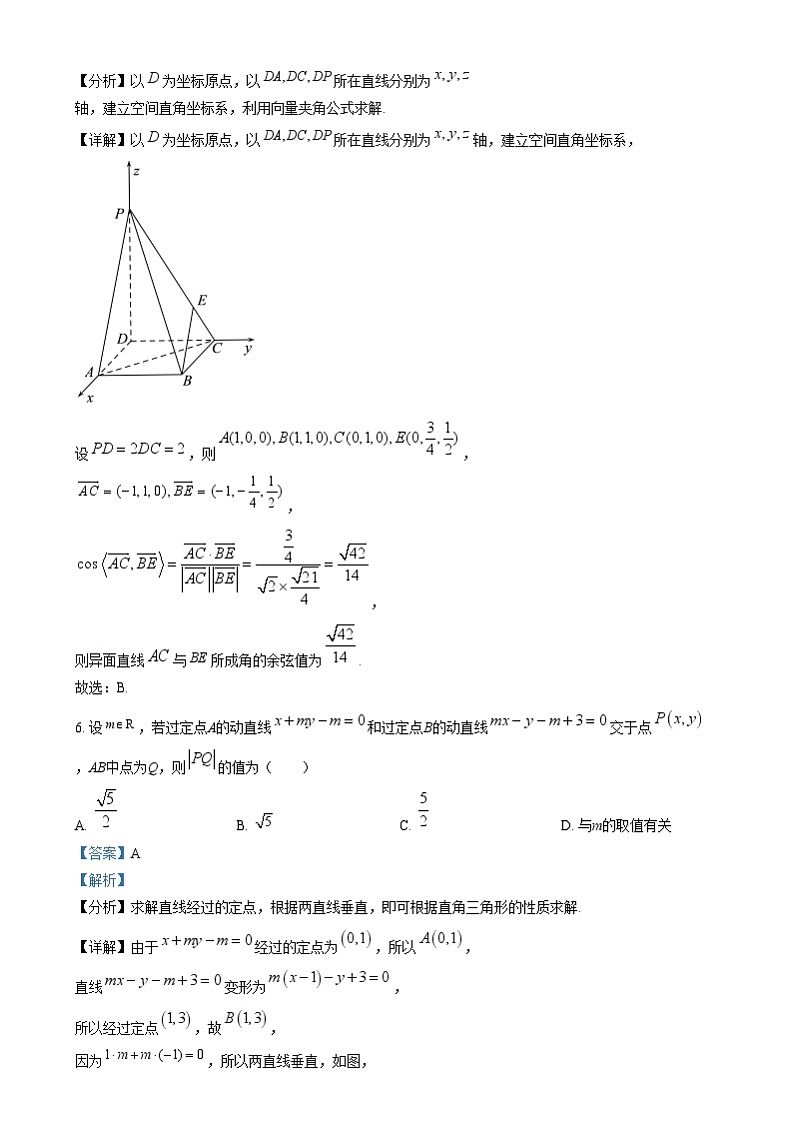
5. 如图，在四棱锥中，底面为正方形，底面，，E为上一点，且，则异面直线与所成角的余弦值为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】以为坐标原点，以所在直线分别为轴，建立空间直角坐标系，利用向量夹角公式求解.
【详解】以为坐标原点，以所在直线分别为轴，建立空间直角坐标系，
设，则，
，
，
则异面直线与所成角的余弦值为.
故选：B.
6. 设，若过定点A的动直线和过定点B的动直线交于点，AB中点为Q，则的值为（ ）
A. B. C. D. 与m的取值有关
【答案】A
【解析】
【分析】求解直线经过的定点，根据两直线垂直，即可根据直角三角形的性质求解.
【详解】由于经过的定点为，所以，
直线变形为，
所以经过定点，故，
因为，所以两直线垂直，如图，
因此为直角三角形，
所以，
故选：A
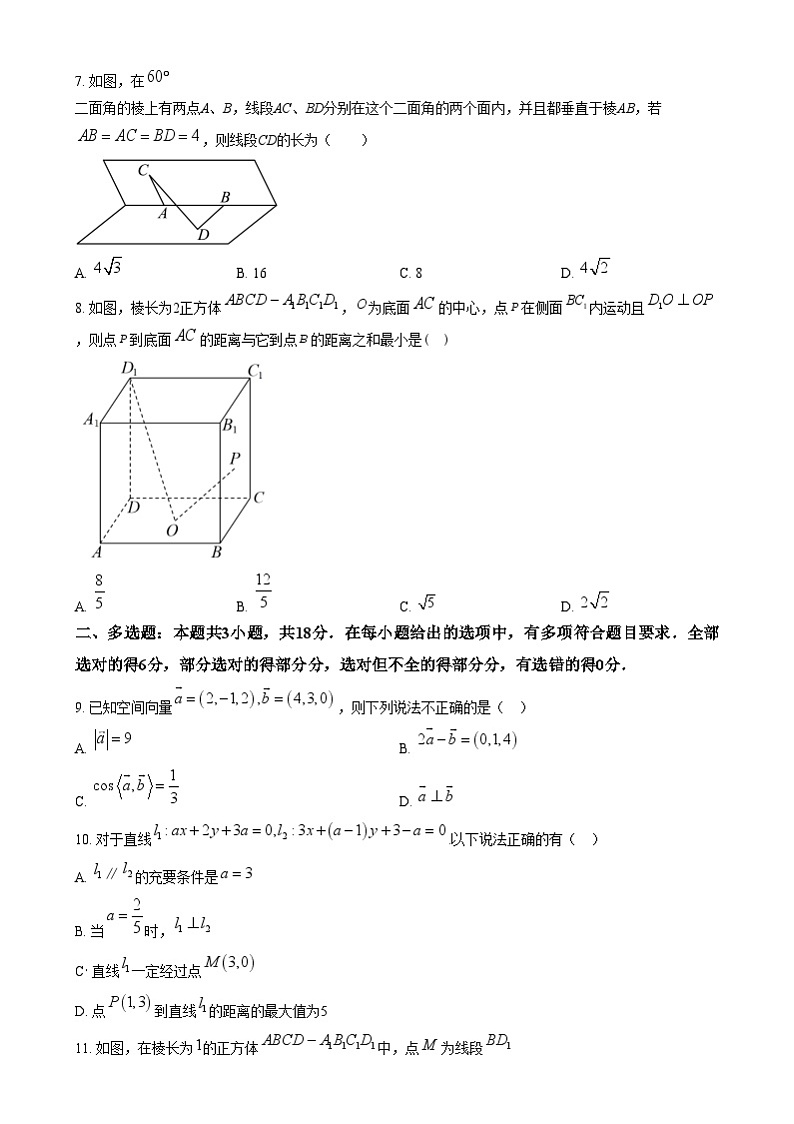
7. 如图，在二面角的棱上有两点A、B，线段AC、BD分别在这个二面角的两个面内，并且都垂直于棱AB，若，则线段CD的长为（ ）
A. B. 16C. 8D.
【答案】D
【解析】
【分析】分别过点、点作、的平行线相交于点，连接，则由题意可知为等边三角形，为直角三角形，求解即可.
【详解】分别过点、点作、的平行线相交于点，连接，
则四边形为平行四边形.
线段AC、BD分别在这个二面角的两个面内，并且都垂直于棱AB.
，则为二面角的平面角，即
，如图所示.
为等边三角形，
，，，平面，平面
平面
又平面
在中
故选：D
【点睛】本题考查空间的距离问题，属于中档题.
8. 如图，棱长为2正方体，为底面的中心，点在侧面内运动且，则点到底面的距离与它到点的距离之和最小是( )
A. B. C. D.
【答案】A
【解析】
【分析】取中点，连接，证明平面，求出P在FC上.将平面沿BC翻折到与平面ABCD共面，将B关于CF对称到，过作与E，则即为点到底面的距离与它到点的距离之和的最小值.
【详解】取中点，连接，
由，，可知，则，
∴由知，即.
∵平面ABCD，⊥平面ABCD，∴AC⊥，又AC⊥BD，BD∩＝B，
∴平面，∵平面，∴，
∵，∴平面，
∵，∴平面，平面，
∵在侧面内，∴平面平面，即P在CF上；
∵平面⊥平面ABCD，且交线为BC，
∴P到平面ABCD的距离即为P到BC的距离，
将平面沿BC翻折到与平面ABCD共面，如图：
将B关于CF对称到，过作与E，则即为点到底面的距离与它到点的距离之和的最小值.
以B为原点，建立如图所示坐标系，则B(0，0)，F(1，0)，C(0，2)，
直线CF方程为，即，
设，则，
∴.
故选：A﹒
二、多选题：本题共3小题，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，选对但不全的得部分分，有选错的得0分．
9. 已知空间向量，则下列说法不正确是（ ）
A. B.
C. D.
【答案】ABD
【解析】
【分析】用空间向量的坐标运算处理即可.
【详解】由，得，故A错误；
，故B错误；
又，故C正确；
，所以与不垂直，故D错误.
故选：ABD.
10. 对于直线.以下说法正确的有（ ）
A. 的充要条件是
B 当时，
C. 直线一定经过点
D. 点到直线的距离的最大值为5
【答案】BD
【解析】
【分析】求出的充要条件即可判断A;验证时，两直线斜率之积是否为-1，判断B;求出直线经过的定点即可判断C;判断何种情况下点到直线的距离最大，并求出最大值，可判断D.
【详解】当时， 解得 或，
当时，两直线为 ，符合题意；
当时，两直线为 ，符合题意，故A错误；
当时，两直线为， ，
所以，故B正确；
直线即直线，故直线过定点，C错误；
因为直线过定点，当直线与点和的连线垂直时，到直线的距离最大，最大值为 ，
故D正确，
故选：BD.
11. 如图，在棱长为的正方体中，点为线段上的动点（含端点），下列四个结论中，正确的有（ ）
A. 存在点，使得平面
B. 存在点，使得直线与直线所成的角为
C. 存在点，使得三棱锥的体积为
D. 不存在点，使得，其中为二面角的大小，为直线与直线所成的角
【答案】ACD
【解析】
【分析】以点为坐标原点，、、所在直线分别为、、轴建立空间直角坐标系，利用空间向量法可判断各选项正误.
【详解】以点为坐标原点，、、所在直线分别为、、轴建立如下图所示的空间直角坐标系，
则、、、、、、
、，设，即点，其中.
对于A选项，假设存在点，使得平面，
，，，则，解得，
故当点为线段的中点时，平面，A对；
对于B选项，，，
由已知可得，则，B错；
对于C选项，，点到平面的距离为，
则，解得，C对；
对于D选项，，，设平面的法向量为，
则，取，可得，
易知平面的一个法向量为，
由图可得，
，，
，
因为，，
则，
、，且余弦函数在上单调递减，则，D对.
故选：ACD.
【点睛】方法点睛：求空间角的常用方法：
（1）定义法：由异面直线所成角、线面角、二面角的定义，结合图形，作出所求空间角，再结合题中条件，解对应的三角形，即可求出结果；
（2）向量法：建立适当的空间直角坐标系，通过计算向量的夹角（两直线的方向向量、直线的方向向量与平面的法向量、两平面的法向量）的余弦值，即可求得结果.
三、填空题：本题共3小题，每小题5分，共15分．
12. 两条平行线与之间的距离为______.
【答案】##0.1
【解析】
【分析】利用平行线间的距离公式计算即可求.
【详解】两条平行线的方程分别为与，
故它们间的距离为.
故答案为：
13. 已知向量，，若，则的值是_____
【答案】##
【解析】
【分析】由向量平行的坐标运算法则，可以解得的值，计算的值得答案.
【详解】因为向量，，且，
所以，
解得，所以.
故答案为：.
14. 如图，正四棱锥模型中，过点作一个平面分别交棱､､于点､､，若，，则_____________.
【答案】##0.75
【解析】
【分析】法一：设，则，结合四点共面，从而得到；
法二：作出辅助线，找到点的位置，求出.
【详解】法一：设，
则有
，
因为四点共面，可设，
故，
即，
故，
故，
法二：如图所示：作法：连接并延长，与的延长线相交于点，
连接并延长，与延长线相交于点，
连接，与相交于一点，则该点即为点.
理由如下：
因为与是两条相交直线，所以与确定一个平面，
则，，A､､，
因为，，所以，
因为，所以，，､､､四点共面.
取的中点，因为，所以平行于，且，
故，故.
故答案为：
四、解答题：本题共5小题，共77分．解答应写出文字说明，证明过程或演算步骤．
15. 已知直线的方程为．
（Ⅰ）直线与垂直，且过点（1，-3），求直线的方程；
（Ⅱ）直线与平行，且直线与两坐标轴围成的三角形的面积为4，求直线的方程．
【答案】（1）（2）直线的方程为：或
【解析】
【详解】试题分析：（1）由直线与垂直，可设直线的方程为：，将点 代入方程解得，从而可得直线的方程；(2)由直线与平行，可设直线的方程，由直线与两坐标轴围成的三角形的面积为，解得可得直线的方程.
试题解析：（1）设直线的方程为：
直线过点（1，-3），
解得
直线的方程为：．
(2)设直线的方程为：
令，得；令，得
则，得
直线的方程为：或．
16. 在平行六面体中，，，．记向量，向量，向量．
（1）取的中点M，用向量来表示向量；
（2）求向量和向量所成角的余弦值．
【答案】（1）
（2）
【解析】
【分析】（1）根据空间向量的线性运算计算即可；
（2）根据空间向量的数量积和模长公式计算即可.
【小问1详解】
【小问2详解】
，，
又，，，
所以，，
所以
；
，
所以，
又
，
所以，所以，
故和所成角的余弦值为.
17. 在如图所示的几何体ABCDFE中，面ABCD是边长为2的正方形，AE⊥面ABCD，DF∥AE，且DFAE＝1，N为BE的中点.M为CD的中点，

（1）求证：FN∥平面ABCD；
（2）求二面角N﹣MF﹣D的余弦值；
（3）求点A到平面MNF的距离.
【答案】（1）证明见解析
（2）
（3）
【解析】
【分析】（1）建立空间直角坐标系，得到，显然平面ABCD的法向量可以为（0，0，1），所以，即，即可得证；
（2）平面MNF的法向量为，平面MFD的法向量可以为（0，1，0），代入公式即可求解；
（3）由（2）知平面MNF的法向量为（2，1，2），又，代入公式即可求解．
【小问1详解】
证明：如图建立空间直角坐标系，

则A（0，0，0），B（2，0，0），D（0，2，0），
E（0，0，2），N（1，0，1），M（1，2，0），F（0，2，1），
所以，显然平面ABCD的法向量可以为（0，0，1），
所以，即，又NF⊄平面ABCD，所以NF∥平面ABCD；
【小问2详解】
因为，
设平面MNF的法向量为（x，y，z），则，
令y＝1，则x＝z＝2，所以，
显然平面MFD的法向量可以为（0，1，0），
设二面角N﹣MF﹣D为，由图可知二面角N﹣MF﹣D为钝角，
则，
所以二面角N﹣MF﹣D的余弦值为；
【小问3详解】
由（2）知平面MNF的法向量为（2，1，2），
又，设点A到平面MNF的距离为d，
则，
所以点A到平面MNF的距离为．
18. △ABC的顶点A的坐标为（1，4），∠B，∠C平分线的方程分别为和.
（1）求BC所在直线的方程.
（2）设，直线过线段的中点M且分别交轴与轴的正半轴于点P、Q，O为坐标原点，求△面积最小时直线的方程；.
【答案】（1）
（2）
【解析】
【分析】（1）求出点A关于两条角分线的对称点，即可求出直线方程；
（2）设直线方程，可得，代入面积，利用基本不等式可得.
【小问1详解】
如图所示，的平分线BD的方程为：，的平分线CE的方程为，
由角平分线的性质知，点A关于直线BD、CE的对称点、必在BC所在的直线上.
由方程组：，解得：，则点的坐标为.
由方程组：，解得：，则点的坐标为.
∴BC所在直线的方程为：，即：；
【小问2详解】
设直线的方程的方程为：，
又直线过点M（2，1），所以，即，
则△的面积，
当且仅当即，时等号成立.
所以，直线的方程为：，即.
19. 如图，已知四棱锥，底面是矩形，，点是棱上一劫点（不含端点）.
（1）求证：平面平面；
（2）当且时，若直线与平面所成的线面角，求点的运动轨迹的长度.
【答案】（1）证明见解析
（2）
【解析】
【分析】（1）根据线面垂直的判定得到平面即可证明；
（2）分别计算和时的情况，根据线面垂直与几何关系确定点的临界位置，进而求得点的运动轨迹的长度即可
【小问1详解】
证明：因为，
故，又
所以平面
平面
所以平面平面
【小问2详解】
首先，取中点，连接等腰中，①
由（1）知平面，得②
由①②得平面，即此时当与点重合时，
直线与平面所成的线面角为，
其次，由题意易得，存在点两侧各有两个点，如图分别记为，使得的运动轨迹即为线
段.
作于，又平面，得，
故平面，
所以在平面的射影为，
即为直线与平面所成的线面角，
即
此时，，此时与重合，
故
同理可得，解得
故的运动轨迹长度为.