2024-2025学年辽宁省鞍山市高三上册12月期末考试数学检测试题（附解析）

这是一份2024-2025学年辽宁省鞍山市高三上册12月期末考试数学检测试题（附解析），共17页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
一、单选题（本大题共8小题）
1．集合，，求（ ）
A．B．C．D．
2．若复数满足，则（ ）
A．3B．2C．D．1
3．“”是“点在圆外”的（ ）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件
4．已知平面向量与的夹角为，，，则的值为（ ）
A．B．C．D．
5．函数中的图像可能是（ ）
A．B．
C．D．
6．的展开式中系数为（ ）
A．180B．90
C．20D．10
7．设抛物线的焦点为，过抛物线上点作准线的垂线，设垂足为，若，则（ ）
A．B．C．D．
8．已知函数满足，则（ ）
A．10000B．10082C．10100D．10302
二、多选题（本大题共3小题）
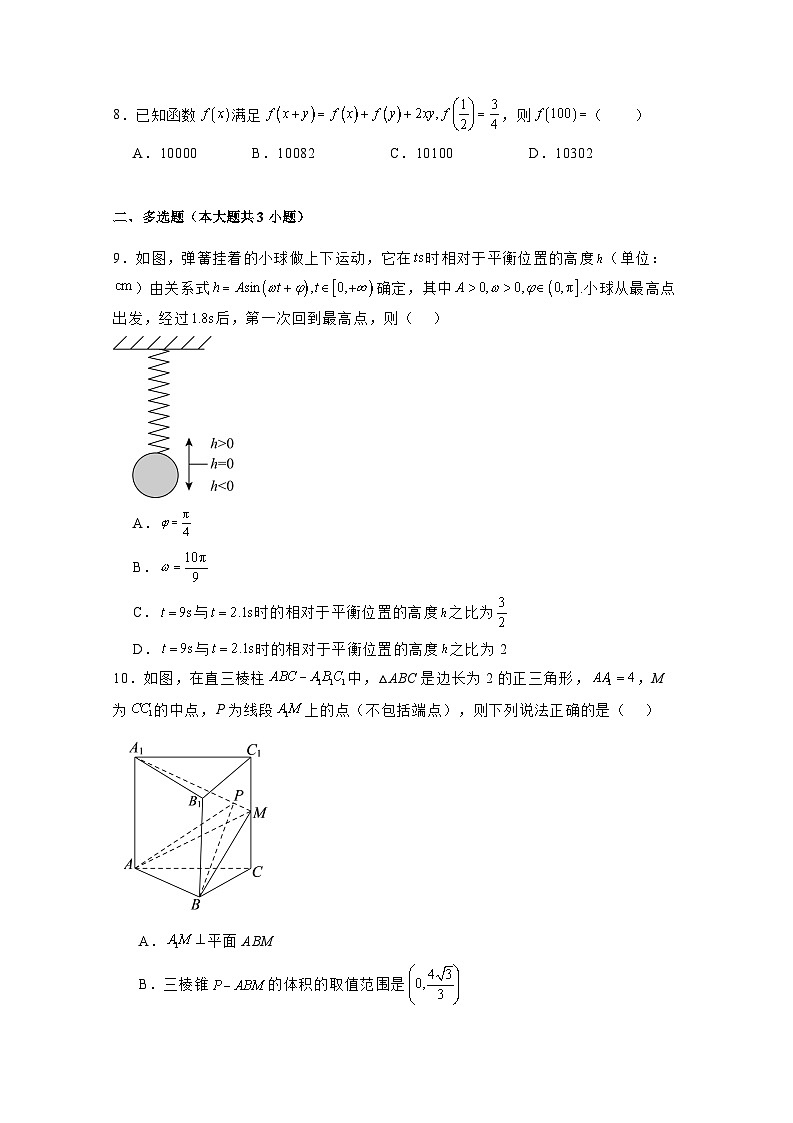
9．如图，弹簧挂着的小球做上下运动，它在时相对于平衡位置的高度（单位：）由关系式确定，其中.小球从最高点出发，经过后，第一次回到最高点，则（ ）

A．
B．
C．与时的相对于平衡位置的高度之比为
D．与时的相对于平衡位置的高度之比为2
10．如图，在直三棱柱中，△ABC是边长为2的正三角形，，M为的中点，P为线段上的点（不包括端点），则下列说法正确的是（ ）
A．平面ABM
B．三棱锥的体积的取值范围是
C．存在点P，使得BP与平面所成的角为60°
D．存在点P，使得AP与BM垂直
11．已知直线分别与函数和的图象交于点，则下列结论正确的是
A．B．
C．D．
三、填空题（本大题共3小题）
12．已知，则的值为 .
13．已知是等差数列，，则 .
14．过双曲线右焦点F的直线l与双曲线C的一条渐近线垂直，垂足为点A，O为坐标原点，若的角平分线与x轴交于点M，且点M到OA与AF的距离都为，则双曲线C的离心率为 ．
四、解答题（本大题共5小题）
15．在中，角A，B，C的对边分别为a，b，c，且.
（1）求角C；
（2）若，求的面积.
16．已知函数，．
(1)若函数在上单调递减，求a的取值范围：
(2)若直线与的图象相切，求a的值．
17．如图，四边形是边长为的菱形，对角线，F为的中点，平面，.现沿将翻折至的位置，使得平面平面，且点和E在平面同侧.
（1）证明：平面；
（2）求二面角大小的正弦值.
18．短视频已成为当下宣传的重要手段，东北某著名景点利用短视频宣传增加旅游热度，为调查某天南北方游客来此景点旅游是否与收看短视频有关，该景点对当天前来旅游的500名游客调查得知，南方游客有300人，因收看短视频而来的280名游客中南方游客有200人.
(1)依据调查数据完成如下列联表，根据小概率值的独立性检验，分析南北方游客来此景点旅游是否与收看短视频有关联：（单位：人）
(2)为了增加游客的旅游乐趣，该景点设置一款5人传球游戏，每个人得到球后都等可能地传给其余4人之一，现有甲,乙等5人参加此游戏，球首先由甲传出.
（i）求经过次传递后球回到甲的概率；
（ii）记前次传递中球传到乙的次数为，求的数学期望.
参考公式：，其中；
附表：
19．已知为坐标原点，动点在椭圆上，动点满足，记点的轨迹为.
(1)求轨迹的方程；
(2)在轨迹上是否存在点，使得过点作椭圆的两条切线互相垂直？若存在，求点的坐标：若不存在，请说明理由：
(3)过点的直线交轨迹于，两点，射线交轨迹于点，射线交椭圆于点，求四边形面积的最大值.
答案
1．【正确答案】C
【详解】由可得，则，
于是.
故选C.
2．【正确答案】C
【详解】由，得，
所以，
所以，
所以.
故选：C.
3．【正确答案】B
【详解】将化为标准方程，得
当点在圆外时，有，解得
∴“”是“点”在圆外”的必要不充分条件.
故选：B.
4．【正确答案】B
【详解】因为，所以，
所以，
所以
，
所以，
故选：B.
5．【正确答案】D
【详解】解：因为定义域为，
又，
所以为奇函数，函数图象关于原点对称，故排除A、B，
又时，，所以，
所以，故排除C；
故选：D
6．【正确答案】A
【详解】展开式通项公式，
其各项次数依次为,
所以的系数是的一次项系数2乘以展开式的的系数.
由展开式通项公式知 解得，
所以系数为.
故选：A.
7．【正确答案】A
【详解】如图所示：
设 为准线与轴的交点，
因为，且，所以，
因为，所以，
而在中，，
所以.
故选：A.
8．【正确答案】C
【详解】中，令得，
，
故，
故，
其中，
，
，
……，
，
上面99个式子相加得，
，
令得，
在中，令得，
故.
故选C.
9．【正确答案】BD
【详解】由题可知小球运动的周期，所以，解得，故B正确；
当时，.
又，所以，故A错误；
则，
所以与时的相对于平衡位置的高度之比为，故C错误，D正确.
故选：BD.
10．【正确答案】BC
【详解】解：由题意得．则， ，
所以与不垂直．故A错误；，点B到平面的距离为，
由，所以，所以，又，
则，故B正确；
BP与平面所成的角即为BP与平面ABC所成的角，设为，易知当点P与M重合时，最小，此时，当点P与重合时，最大，此时，，此时，故存在点P，使得BP与平面所成的角为60°，故C正确；
若，设中点为，所以，又平面平面，平面平面，平面，所以平面，平面，所以，又，则平面，因为平面，所以，因为，，故与不垂直，故不合题意，故D错误．
故选：BC
11．【正确答案】ABC
【详解】函数与互为反函数，
则与的图象关于对称，
将与联立，则，
由直线分别与函数和的图象交于点，
作出函数图像：

则的中点坐标为，
对于A，由，解得，故A正确；
对于B，，
因为，即等号不成立，所以，故B正确；
对于C，将与联立可得，即，
设，且函数为单调递增函数，
，，
故函数的零点在上，即，由，则，
，故C正确；
对于D，由，解得，
由于，则，故D错误；
故选：ABC
12．【正确答案】
【详解】因，则，
.
故
13．【正确答案】3
【详解】因为，所以，
因为，
所以.
故3.
14．【正确答案】
【详解】由题意得，双曲线的渐近线为，，如图，
设点A在第一象限，则点F到渐近线的距离为，
所以，
过点M分别作于点N，于点T，
又于A，所以四边形MTAN为正方形，得，
所以，又，
所以，得，则，
所以，故，
即双曲线的离心率为.
故答案为.
15．【正确答案】（1）；（2）．
【详解】（1）因为，由正弦定理得，即，
所以，，所以；
（2）由（1），，而，
所以，
．
16．【正确答案】(1)
(2)
【详解】（1）记在上单调递减，
对恒成立，
，而，
当且仅当即时，等号成立，
所以当时，取得最小值为.
所以a的取值范围为
（2）设直线与的图象相切于，
，
由题意可知，
代入，
，左边式子关于单调递减且时，左边
17．【正确答案】（1）证明见解析；（2）.
【详解】（1）取中点O，连，∴F为的中点，∴，又面面.
∴平面，，∴，
又∵平面平面，平面平面.
∴平面，又平面，∴.
又平面，平面，∴平面，平面.
∴平面平面，
因为平面，所以平面.
（2）以O为坐标原点，所在直线为x，y，z轴，建立如图所示的空间直角坐标系.
设平面的法向量为.
∴
令，则
设平面的法向量为.
∴
令，则.
∴.
∴二面角的正弦值为.
18．【正确答案】(1)列联表见解析，无关
(2)（i）；（ii）
【详解】（1）将所给数据进行整理，得到如下列联表：
零假设：南北方游客来此景点旅游与短视频无关联．
，
根据小概率值的独立性检验，我们推断不成立，
即认为南北方游客来此景点旅游与收看短视频有关联，此推断犯错误的概率不大于0.001.
（2）（i）设经过次传递后回到甲的概率为，
，，
又，
所以是首项为，公比为的等比数列，
所以.
（ii）（方法一）设第次传递时甲接到球的次数为，则服从两点分布，，
设前次传递中球传到甲的次数为，
，
因为，所以.
（方法二）设第次传递时，乙接到球的概率和次数分别为与，则服从两点分布，
，由题可知，，
又，所以，所以是首项为，公比为的等比数列，
，，
，
故.
19．【正确答案】(1)
(2)存在，或(
(3)
【详解】（1）设则，
由得，
又在椭圆上，所以
代入化简得，
所以点的轨迹的方程为
（2）当两条切线的斜率存在时，设过点的切线为，
联立，消去得
则由判别式，得，
设两条切线的斜率分别为，依题意得
即，
又点在轨迹上，所以，解得，
所以或(
当两条切线的斜率有一条不存在时，结合图象得不合题意，
综上，存在满足条件的点，且点的坐标为或(.
（3）将代入轨迹的方程，
可得，
由，
可得①，且，，
所以，
因为直线与轴交点的坐标为，
所以的面积
，
将代入椭圆C的方程可得，
由，可得②，
令，由①②可知，
因此，故，
当且仅当，即时，取得最大值2，
由题知的面积，又易知面积，
从而四边形的面积，
所以四边形的面积的最大值为.
游客
短视频
合计
收看
未看
南方游客
北方游客
合计
0.1
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828
游客
短视频
合计
收看
未看
南方游客
200
100
300
北方游客
80
120
200
合计
280
220
500