2024-2025学年四川省成都市高二上册12月月考数学检测试题（附解析）

这是一份2024-2025学年四川省成都市高二上册12月月考数学检测试题（附解析），共17页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
一、单选题（本大题共8小题）
1．过点，且倾斜角为的直线方程为（ ）
A．B．C．D．
2．某市年深入实施创新驱动发展战略，新产业新产品增势良好．调研统计了家企业，得到了他们的科技创新月平均新增收益如下：（单位：百万元），则其百分位数是（ ）
A．B．C．D．
3．已知空间向量，，若，则（ ）
A．B．C．D．
4．与椭圆共焦点，且与双曲线共渐近线的双曲线的方程为（ ）
A．B．C．D．
5．如图，空间四边形OABC中，，点M在线段OA上，且，点N为BC中点，则（ ）
A．B．
C．D．
6．有一组数据：2，4，5，7，6，7，x，10，这组数据的平均数为6，则这组数据的方差为（ ）
A．5B．6C．7D．8
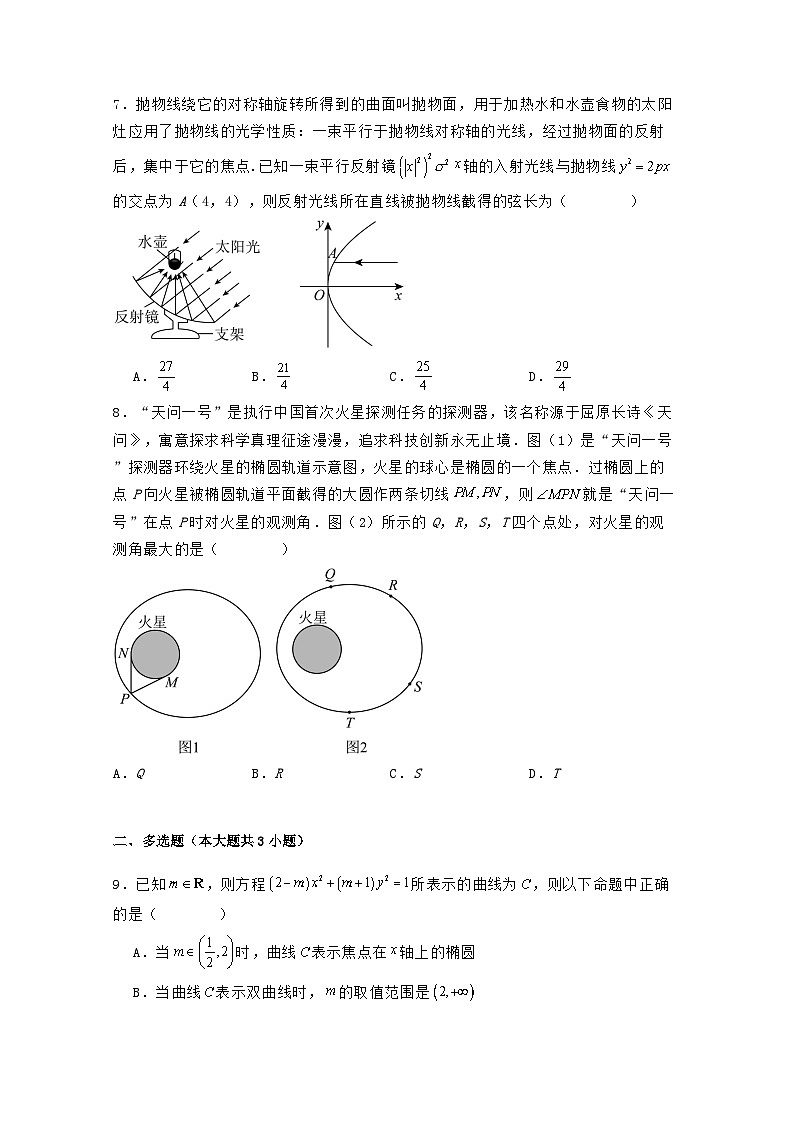
7．抛物线绕它的对称轴旋转所得到的曲面叫抛物面，用于加热水和水壶食物的太阳灶应用了抛物线的光学性质：一束平行于抛物线对称轴的光线，经过抛物面的反射后，集中于它的焦点.已知一束平行反射镜轴的入射光线与抛物线的交点为A（4，4），则反射光线所在直线被抛物线截得的弦长为（ ）

A．B．C．D．
8．“天问一号”是执行中国首次火星探测任务的探测器，该名称源于屈原长诗《天问》，寓意探求科学真理征途漫漫，追求科技创新永无止境．图（1）是“天问一号”探测器环绕火星的椭圆轨道示意图，火星的球心是椭圆的一个焦点．过椭圆上的点P向火星被椭圆轨道平面截得的大圆作两条切线，则就是“天问一号”在点P时对火星的观测角．图（2）所示的Q，R，S，T四个点处，对火星的观测角最大的是（ ）
A．QB．RC．SD．T
二、多选题（本大题共3小题）
9．已知，则方程所表示的曲线为，则以下命题中正确的是（ ）
A．当时，曲线表示焦点在轴上的椭圆
B．当曲线表示双曲线时，的取值范围是
C．当时，曲线表示两条直线
D．存在，使得曲线为等轴双曲线
10．设是两个随机事件，若，则下列结论正确的是（ ）
A．若，则B．若，则
C．若，则相互独立D．若相互独立，则
11．在正方体中，，点是的中点，空间中一点满足，则（ ）
A．当时，
B．当时，三棱锥的体积为定值
C．当时，有且仅有一个点，使得平面
D．当时，有且仅有一个点，使得与所成角为
三、填空题（本大题共3小题）
12．已知抛物线，则其焦点到准线的距离为 ．
13．如图是某个闭合电路的一部分，每个元件的可靠性是，则从到这部分电路畅通的概率为 ．
14．已知双曲线 的右焦点为，过点作直线与渐近线 垂直，垂足为点，延长交于点.若，则的离心率为 .
四、解答题（本大题共5小题）
15．已知抛物线，其焦点F到其准线的距离为2，过焦点F且倾斜角为45°的直线l交抛物线C于A，B两点，
(1)求抛物线C的方程及其焦点坐标；
(2)求．
16．已知动点P与平面上两定点连线的斜率的积为定值，试求：
(1)动点P的轨迹C的方程；
(2)是否存在过点与（1）中曲线C相交所得弦长的直线，若存在，求直线l的方程；若不存在，试说明理由.
17．如图，在四棱锥中，平面，，，且，，M是AD的中点，N是AB的中点．
(1)求证：平面ADE；
(2)求直线CM与平面DEN所成角的正弦值．
18．在平面直角坐标系中，已知圆和圆．

(1)若直线过点，且与圆相切，求直线的方程；
(2)设为直线上的点，满足：过点的无穷多对互相垂直的直线和，它们分别与圆和圆相交，且直线被圆截得的弦长与直线被圆截得的弦长相等．试求满足条件的点的坐标．
19．一般地，我们把平面内与两个定点的距离的差的绝对值等于非零常数（小于）的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点，两焦点的距离叫做双曲线的焦距.
(1)请用上述定义证明反比例函数的图象是双曲线；
(2)利用所学的知识，指出双曲线的焦点坐标与渐近线方程；
(3)我们知道，双曲线上的任意一点到与的距离之积是常数，即.探讨双曲线上的任意一点是否有类似结论，若有，写出结论并证明；若没有，则说明理由.
答案
1．【正确答案】A
【详解】因为过点的直线倾斜角为，
即直线垂直于轴，所以直线方程为.
故选：A
2．【正确答案】C
【详解】因为，
所以从小到大排列取第个数为．
故选：C．
3．【正确答案】B
【详解】由，知，使得，
即，
所以，解得，所以．
故选：B
4．【正确答案】A
【详解】因为椭圆，焦点在y轴上，且，
又因为所为双曲线与双曲线共渐近线，
所以设所求双曲线，即
则，解得.
所以所求双曲线为.
故选：A
5．【正确答案】D
【详解】点M在线段OA上，且，
又，
∵N为BC的中点，
.
故选：D.
6．【正确答案】A
【详解】依题意，，解得，
所以组数据的方差为.
故选：A
7．【正确答案】C
【分析】由题意可以求出抛物线的方程，再根据光线的反射性质求出反射光线的方程，即可求出反射光线与抛物线的交点坐标，再利用两点间的距离公式即可得出答案.
【详解】因为点在抛物线上，
所以 ，解得 ，
所以抛物线方程为 .
故抛物线的焦点为 ，
又因为反射光线经过点 及焦点 ，
所以反射光线AB的方程为 ，
联立抛物线方程得 ，解得 或 ，
故反射光线 AB 与抛物线的交点为 ，
由两点距离公式得
所以反射光线所在直线被抛物线截得的弦长为.
故选C.

8．【正确答案】A
【分析】连接点P和椭圆的左焦点，由对称性和椭圆上点到焦点距离的特征得点P位于条件中点Q处，对火星的观测角最大.
【详解】
设火星半径为R，椭圆左焦点为，连接，则，
因为，所以越小，越大，越大，
所以当点P位于条件中点Q处，对火星的观测角最大.
故选：A.
9．【正确答案】AC
【详解】对于A，当时，，
表示焦点在轴上的椭圆，即曲线表示焦点在轴上的椭圆，故选项正确；
对于，若曲线表示双曲线，则，解得或，
即实数的取值范围为，故选项B错误；
对于，当时，曲线，即，
即曲线表示两条直线，故选项C正确；
对于，若曲线为等轴双曲线，则，解集为，
不存在，使得曲线为等轴双曲线，故选项D错误．
故选：AC．
10．【正确答案】AC
【详解】对于A，若，则，A正确；
对于B，若，则事件互斥，
所以，B错误；
C选项，因为，所以，则相互独立，C正确；
D选项，若相互独立，则相互独立，且，
所以，D错误．
故选：AC．
11．【正确答案】AC
【详解】对于选项A，当时，，
如图所示，

根据平面向量基本定理，此时P在线段上，
由于在正方体中，平面，平面，
所以，选项A正确；
对于选项B，当时，，
如图所示，

由平面向量基本定理，此时P在线段上，
由图可知，三棱锥当以平面为底面时为定值，
但因为顶点P在线段上运动，所以P到底面的高不确定，
故三棱锥的体积不是定值，选项B错误；
对于选项C，当时，如图所示，

此时，
由平面向量基本定理，取AB与中点M，N，则P在线段MN上运动，
由图可知，过B点且与平面平行的平面为平面，
平面，所以此时平面，
又P是MN与交点，即当且仅当P是MN中点时，有平面，
故选项C正确；
对于选项D，如图所示，

以D为原点，DC，DA，分别为x，y，z轴建立空间直角坐标系，
则，
因为，则有，
又，
所以，
所以.
于是，，
所以的夹角为时有，
，
解得或，
即或都可以使得的夹角为，
选项D错误.
故选：AC.
12．【正确答案】/0.25
【详解】由 得 ，
所以抛物线的焦点到准线的距离.
故
13．【正确答案】
【详解】上半部分电路畅通的概率为：，
下半部分电路畅通的概率为，上下两部分并联，畅通的概率为：．
故答案为.
14．【正确答案】/
【详解】设为坐标原点，则，
从而.

设的左焦点为，连接，
由双曲线的定义，得.
在中，由余弦定理，得，
解得.
由，得，解得，
所以.
故答案为.
15．【正确答案】(1)抛物线C的方程为．焦点坐标为．
(2)8
【分析】（1）根据焦点F到其准线的距离求出，即可求出抛物线C的方程及其焦点坐标.
（2）根据直线l过焦点F且倾斜角为45°，得出直线l的方程，让直线l与抛物线方程联立，消去y，设出A，B两点坐标，根据抛物线的定义即可求出.
【详解】（1）由题意在抛物线中，焦点F到其准线的距离为2，
∴，
∴抛物线C的方程为，焦点坐标为．
（2）由题意及（1）得
在抛物线中，过焦点F且倾斜角为45°的直线l的方程为，
∴联立方程组消去y可得，
设，，则，
∴根据抛物线的定义，．
16．【正确答案】(1)；
(2)存在，或.
【详解】（1）设动点，
由题意，化简整理得，
故点P的轨迹C的方程是.
（2）直线斜率不存在时不合题意，
斜率存在时，设直线与曲线C的交点为，
由，得，，
则，，
，整理得，解得或（舍）.
经检验，符合题意，直线l的方程为，即或.
17．【正确答案】(1)证明见解析；
(2)
【详解】（1）证明：因为平面，平面，所以，
由，知，，
又，平面，所以平面，
因为平面，所以，
因为，是的中点，所以，
又，平面，
所以平面．
（2）平面，，以为坐标原点，
以，，所在直线分别为，，轴，建立如图所示的空间直角坐标系，
则，，，，，，，
故，，，
设平面的法向量，
则，令，则，
设直线与平面所成角为，
则，
即直线与平面所成角的正弦值．
18．【正确答案】(1)或
(2)
【分析】（1）直线斜率不存在时，显然满足题意；当斜率存在时，设，利用圆心到直线距离等于半径可构造方程求得，由此可得切线方程；
（2）设点，当直线斜率存在时，根据截得弦长相等可求得的值；当斜率为时，易知不满足题意；当直线斜率存在且不为时，假设直线方程，根据垂径定理表示出直线被圆截得的弦长，根据有无数个解可确定的取值.
【详解】（1）由圆的方程知：圆心，半径；
当直线斜率不存在时，即，此时直线与圆显然相切，满足题意；
当直线斜率存在时，设其方程为：，即，
圆心到直线的距离，解得：，
直线方程为：，即；
综上所述：直线方程为或.
（2）由圆的方程知：圆心，半径；
设点，
①当过的直线斜率不存在时，则方程为：，方程为：；
则被圆截得的弦长为：；
被圆截得的弦长为，解得：或；
或；
②当过的直线斜率为时，直线斜率不存在，此时与圆相离，不合题意；
③当过的直线斜率存在且不为时，
设，则，
即，，
圆心到直线的距离；圆心到直线的距离；
直线被圆截得的弦长与直线被圆截得的弦长相等，
，即，，
又，，，，
当时，整理可得：，
满足题意的直线有无数对，，解得：，即；
当时，整理可得：，
满足题意的直线有无数对，，方程组无解；
综上所述：满足条件的点的坐标为.
19．【正确答案】(1)证明见解析
(2)焦点：；准线：和
(3)答案见解析
【详解】（1）证明：观察图象可知若函数的图象是双曲线，则它一定是等轴双曲线，
且轴､轴是图象的渐近线，直线是双曲线的对称轴，
它与双曲线的两个交点是双曲线的两个顶点，实轴长.
两焦点坐标为.
设点Px,y在函数的图象上，则，即，
（i）当时，，
所以
.
（ii）当时，从而，同理，有.
因此，无论点Px,y在第一象限或者在第三象限，均有||（小于）.
综上，函数的图象是双曲线.
（2）函数的图象是以为两焦点，实轴长的双曲线，两渐近线方程分别为和.
（3）因为与是双曲线的两条渐近线，有.
类似地：双曲线上的任意一点到它的两条渐近线的距离之积是常数.
证明：设是双曲线上任意一点，则有.
双曲线的渐近线方程为.
于是点到双曲线的两条渐近线的距离之积为，结论成立.