2023~2024学年江苏省常州市七年级上学期期末数学试卷（解析版）

这是一份2023~2024学年江苏省常州市七年级上学期期末数学试卷（解析版），共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1. 下列各数中，是无理数的是（ ）
A. B. C. 3.14D. 0.010010001
【答案】B
【解析】A、是分数，是有理数，不是无理数，故该选项是错误的；
B、是无限不循环小数，是无理数，故该选项是正确的；
C、3.14是有限小数，不是无理数，故该选项是错误的；
D、0.010010001是有限小数，不是无理数，故该选项是错误的；
故选：B
2. 计算的结果是（ ）
A. 3B. 2C. D.
【答案】C
【解析】，
故选：C．
3. 百米大赛的成绩差异总在毫厘之间，裁判经常会依据视频回放帮助自己作出正确的判断，下图大致反映了场上运动员的（ ）
A. 主视图B. 左视图C. 右视图D. 俯视图
【答案】D
【解析】依题意，该图主要反映了场上运动员俯视图；
故选：D．
4. 某地连续四天的天气情况如下，其中温差最大的一天是（ ）
A. 17日B. 18日C. 19日D. 20日
【答案】B
【解析】7日的温差为：；
18日的温差为：；
19日的温差为：；
20日的温差为：；
温差最大的是18日，
故选：B
5. 一个两位数的个位数字是，十位数字是，则这个两位数可表示为（ ）
A. abB. C. D.
【答案】D
【解析】根据题意知，这个两位数可表示为：．
故选：D．
6. 下列各选项中的图形绕虚线旋转一周后，得到的几何体是圆柱的是（ ）
A. B. C. D.
【答案】C
【解析】A、图形绕虚线旋转一周后，得到的几何体是球体，故不符合题意；
B、图形绕虚线旋转一周后，得到几何体是圆锥，故不符合题意；
C、图形绕虚线旋转一周后，得到的几何体是圆柱，故符合题意；
D、图形绕虚线旋转一周后，得到的几何体是圆台，故不符合题意；
故选：C．
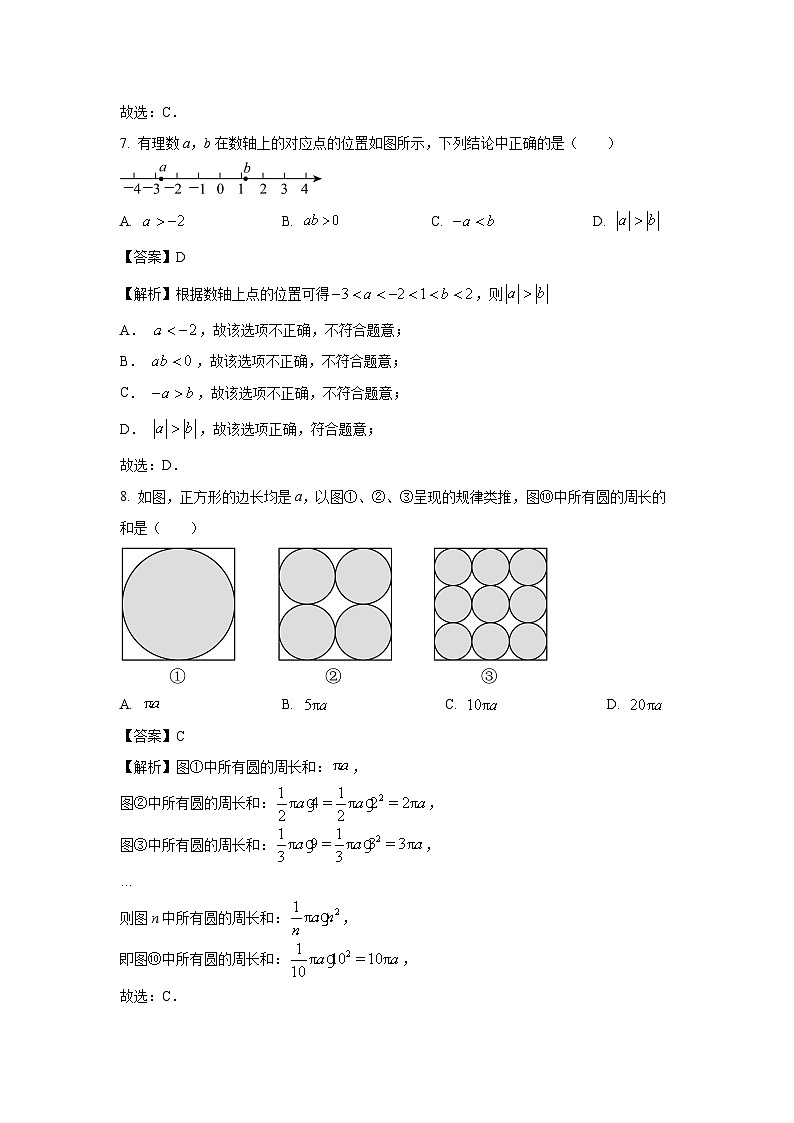
7. 有理数a，b在数轴上的对应点的位置如图所示，下列结论中正确的是（ ）

A. B. C. D.
【答案】D
【解析】根据数轴上点的位置可得，则
A． ，故该选项不正确，不符合题意；
B． ，故该选项不正确，不符合题意；
C． ，故该选项不正确，不符合题意；
D． ，故该选项正确，符合题意；
故选：D．
8. 如图，正方形的边长均是a，以图①、②、③呈现的规律类推，图⑩中所有圆的周长的和是（ ）
A. B. C. D.
【答案】C
【解析】图①中所有圆的周长和：，
图②中所有圆的周长和：，
图③中所有圆的周长和：，
…
则图n中所有圆的周长和：，
即图⑩中所有圆的周长和：，
故选：C．
二、填空题（本大题共8小题，每小题2分，共16分）
9. ﹣3的相反数是__________．
【答案】3
【解析】一个数的相反数就是在这个数前面添上“﹣”号．
所以﹣（﹣3）=3，
故答案为：3．
10. 比较大小： _______（填“”、“”或“”）．
【答案】
【解析】∵
∴
即
故答案为：．
11. 年月日，常州地铁5号线宣布开工，地铁5号线全长约为米．数据用科学记数法表示为______．
【答案】
【解析】，
故答案为：．
12. 若单项式与是同类项，则的值是______．
【答案】5
【解析】∵单项式与是同类项，
∴，，
∴，
故答案：5．
13. 若是关于x的一元一次方程的解，则______．
【答案】3
【解析】将代入关于x的一元一次方程，
得，解得，
故答案为：3．
14. 如图，已知点O在直线AB上，，则______．
【答案】30°
【解析】∵∠AOC与∠BOC互为邻补角，
∴∠AOC＋∠BOC＝180°，①
又∵∠AOC＝5∠BOC，②
把②代入①，可得5∠BOC＋∠BOC＝180°，
解得∠BOC＝30°．
故答案为：30°．
15. 当x分别取、0、1、2时，代数式对应的值如下表：
则b的值是______．
【答案】1
【解析】观察表格可得，当时，，即，
∴，
故答案为：1．
16. 定义：C是线段上的一点，若点C将分得的两条线段中，有一条线段的长与的长的和是10，则称点C是线段的“圆满分割点”．已知，P、Q分别是线段的“圆满分割点”，则的长是______．
【答案】2或4
【解析】∵，P是线段的“圆满分割点”，
∴或
∵Q线段的“圆满分割点”，
∴，
∴或，
综上所述：的长是2或4，
故答案为：2或4．
三、解答题（本大题共9小题，共68分．第17、19、21、22、23、24、25题每题8分，第18、20题每题6分）
17. 计算：
（1）；
（2）．
解：（1）；
（2）．
18. 先化简，再求值：，其中．
解：
，
又因为，，
所以，原式．
19. 解方程：
（1）；
（2）．
解：（1），
移项，得，
合并同类项，得，
系数化成1，得；
（2），
去分母，得，
去括号，得，
移项，得，
合并同类项，得，
系数化成1，得．
20. 如图，点A、B、C均在格点上．
（1）根据下列要求画图：
①找一格点P，使得；
②过点作，垂足为．
（2）在（1）的条件下，垂线段______的长度就是点到的距离．
解：（1）①如图，点P即为所求；
②如图，点Q即为所求；
（2）在（1）的条件下，垂线段的长度就是点到的距离．
故答案为：．
21. 甲、乙两人分别用面值为100元和50元的人民币购买一本同样的书，甲找回的钱是乙找回钱的6倍，求这本书的价格．
解：（1）设这本书的价格为x元．根据题意，得
，
解方程，得，
答：这本书的价格为元．
22. 数学课上，老师给出如下问题：
直线、相交于点O，，平分，射线，求的度数．
小丽：以下是我的解答过程（部分空缺）．
解：如图1，因为射线，所以．
因为与互补，，所以．
因为平分，所以．
因为是直线下方的一条射线，所以．
（1）请补全小丽的解答过程；
（2）小聪说：“小丽的解答并不完整，符合题意的图形还有一种情况．”请在图2中画出小聪说的另一种情况，并解答．
解：（1）如图1所示，
因为射线，所以．
因为与互补，，所以．
因为平分，所以．
因为是直线下方的一条射线，所以；
故答案为：，，，．
（2）如图所示，
因为射线，所以．
因为与互补，，所以．
因为平分，所以．
因为是直线下方的一条射线，所以．
23. 如图，三棱锥的四个顶点处都填写着一个数，其中，点A处填写的数是1．现要求：
围成三棱锥的各个面（左面、右面、后面、底面）的三个顶点处的数之和均相等．
（1）请在图中的点B、C、D处，填写一组符合要求的数；
（2）在点B、C、D处，是否还有其它符合要求的数（与第（1）问的答案不一样）？若有，请指出它们的一般规律；若没有，请说明理由．
解：（1）答案如图：
故答案为：1,1,1．
（2）没有．理由如下：
设点B、C、D处的数字为x，y，z．
由题意得．
解得，
故没有其它的解．
24. 【问题背景】
如图1，小华在荡秋千，秋千底座从点A到点B的过程中，绳子的长度保持不变．在线段、、中，长度最短的是______．

图1
【尝试说理】
我们将会学习不等式的一个性质：如果，那么．根据这个性质和学过的基本事实，可以证实上述结论．
连接、．
根据基本事实“直线外一点与直线上各点连接的所有线段中，______”，可得．
再根据基本事实“______”，可得．
所以，即．
又因为，所以．同理可得．
【方法迁移】
图2是摩天轮的示意图，、是摩天轮的两根支架，、都是摩天轮的半径，且．，，垂足分别为、，经过圆心．小华发现，请根据学过的基本事实，证实这个发现．
解：【问题背景】线段PQ．
【尝试说理】垂线段最短；两点之间线段最短．
【方法迁移】连接，如图，
由基本事实“两点之间线段最短”，
得到，
根据基本事实“垂线段最短”，
得到：，
因此，
因为，
所以，
因此．
25. 如图，在的内部绕点O自由旋转，旋转过程中、的大小始终保持不变，其中．首先绕点O顺时针匀速旋转，旋转速度为每秒，旋转开始前与重合，当旋转至与重合时，立即再以另一速度绕点O逆时针匀速旋转，当旋转至与重合时，旋转停止，设时间为t秒，记，W用含t的代数式表示，已知绕点O顺时针匀速旋转过程中，当和时，与之对应的W的两个值互为相反数；从开始旋转到最后停止，整个过程总用时秒．
（1）绕点O顺时针匀速旋转过程中，W的值的变化情况：______（填“由负到正”或“由正到负”）；
（2）求的大小及逆时针旋转时的速度；
（3）在整个旋转过程中，若，直接写出t的值．
解：（1）绕点O顺时针匀速旋转过程中，从逐渐增大到，从逐渐减小到，
∵，
∴的值的变化情况是由负到正．
故答案为：由负到正．
（2）设的度数为，
当时，，
当时，，
根据题意得，，
，
，
，
∴,
∵，
∴逆时针旋转时的速度为．
答：的大小为，逆时针旋转时的速度为每秒．
（3）当时，、，
，解得:；
当时，、，
，解得: ．
答：当W=60时，t值为或18．
17日
18日
19日
20日
－8~－5℃多云
－4~1℃小雨
0~2℃晴
2~5℃晴
x
…
0
1
2
…
…
1
3
5
…