中考数学三轮考前专项冲刺练习：二次函数（含答案解析）

这是一份中考数学三轮考前专项冲刺练习：二次函数（含答案解析），共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．已知二次函数的图象如图所示，则反比例函数与一次函数在同一平面直角坐标系内的图象可能是（ ）
A．B．C．D．
2．（2021·陕西中考真题）下表中列出的是一个二次函数的自变量x与函数y的几组对应值：
下列各选项中，正确的是（ ）
A．这个函数的图象开口向下 B．这个函数的图象与x轴无交点
C．这个函数的最小值小于-6 D．当时，y的值随x值的增大而增大
3．在平面直角坐标系中，将抛物线y＝x2﹣（m﹣1）x+m（m＞1）沿y轴向下平移3个单位．则平移后得到的抛物线的顶点一定在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
4．已知点A（1，y1），B（2，y2）在抛物线y=-（x+1）2+2上，则下列结论正确的是（ ）
A．2>y1>y2B．2>y2>y1C．y1>y2>2D．y2>y1>2
5．已知二次函数（为常数）的图象与轴有交点，且当时，随的增大而增大，则的取值范围是（ ）
A．B．C．D．
6．（2021·浙江中考真题）已知抛物线与轴的交点为和，点，是抛物线上不同于的两个点，记的面积为的面积为．有下列结论：①当时，；②当时，；③当时，；④当时，．其中正确结论的个数是（ ）
A．1B．2C．3D．4
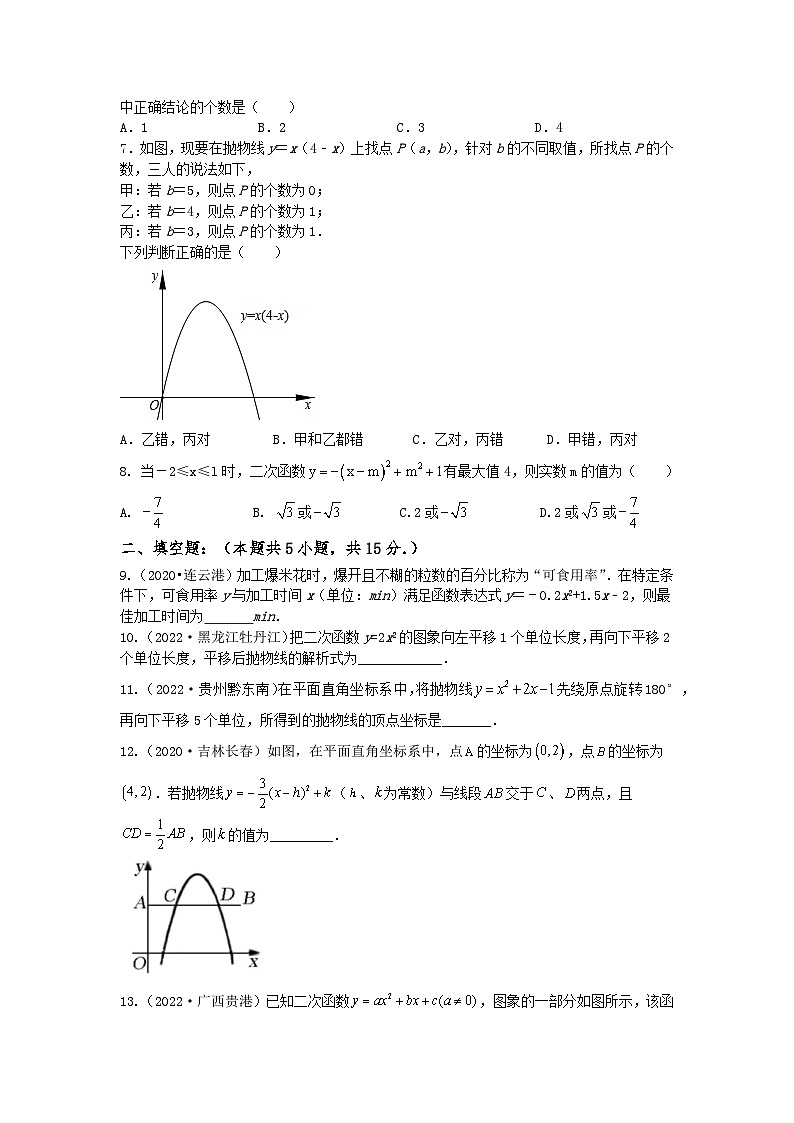
7．如图，现要在抛物线y＝x（4﹣x）上找点P（a，b），针对b的不同取值，所找点P的个数，三人的说法如下，
甲：若b＝5，则点P的个数为0；
乙：若b＝4，则点P的个数为1；
丙：若b＝3，则点P的个数为1．
下列判断正确的是（ ）
A．乙错，丙对B．甲和乙都错C．乙对，丙错D．甲错，丙对
8. 当－2≤x≤l时，二次函数有最大值4，则实数m的值为（ ）
A. B. 或 C.2或 D.2或或
二、填空题：（本题共5小题，共15分．）
9.（2020•连云港）加工爆米花时，爆开且不糊的粒数的百分比称为“可食用率”．在特定条件下，可食用率y与加工时间x（单位：min）满足函数表达式y＝﹣0.2x2+1.5x﹣2，则最佳加工时间为 min．
10.（2022·黑龙江牡丹江）把二次函数y=2x2的图象向左平移1个单位长度，再向下平移2个单位长度，平移后抛物线的解析式为____________．
11.（2022·贵州黔东南）在平面直角坐标系中，将抛物线先绕原点旋转180°，再向下平移5个单位，所得到的抛物线的顶点坐标是_______．
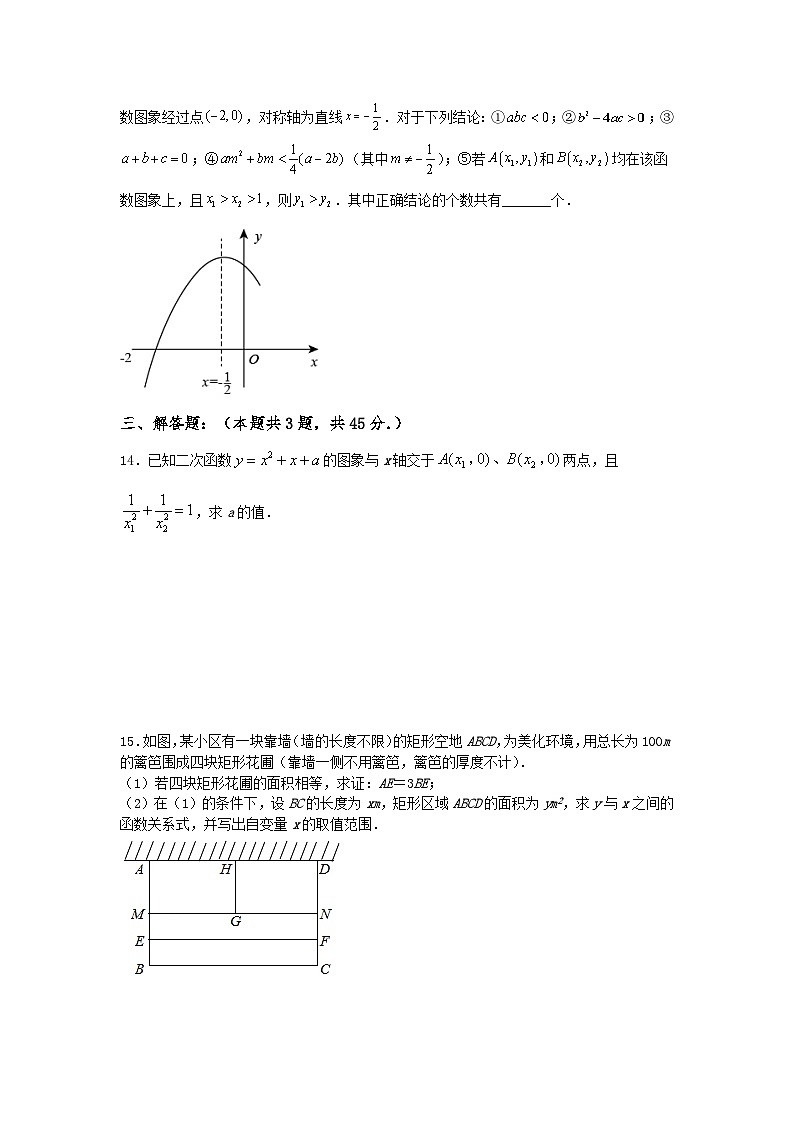
12.（2020·吉林长春）如图，在平面直角坐标系中，点的坐标为，点的坐标为．若抛物线（、为常数）与线段交于、两点，且，则的值为_________．
13.（2022·广西贵港）已知二次函数，图象的一部分如图所示，该函数图象经过点，对称轴为直线．对于下列结论：①；②；③；④（其中）；⑤若和均在该函数图象上，且，则．其中正确结论的个数共有_______个．
三、解答题：（本题共3题，共45分．）
14．已知二次函数的图象与x轴交于两点，且，求a的值．
15．如图，某小区有一块靠墙（墙的长度不限）的矩形空地ABCD，为美化环境，用总长为100m的篱笆围成四块矩形花圃（靠墙一侧不用篱笆，篱笆的厚度不计）．
（1）若四块矩形花圃的面积相等，求证：AE＝3BE；
（2）在（1）的条件下，设BC的长度为xm，矩形区域ABCD的面积为ym2，求y与x之间的函数关系式，并写出自变量x的取值范围．
16．如图，二次函数y＝x2+bx的图象与x轴正半轴交于点A，平行于x轴的直线l与该抛物线交于B、C两点（点B位于点C左侧），与抛物线对称轴交于点D（2，﹣3）．
（1）求b的值；
（2）设P、Q是x轴上的点（点P位于点Q左侧），四边形PBCQ为平行四边形．过点P、Q分别作x轴的垂线，与抛物线交于点P'（x1，y1）、Q'（x2，y2）．若|y1﹣y2|＝2，求x1、x2的值．
…
-2
0
1
3
…
…
6
-4
-6
-4
…
参考答案：
1.C 2.C 3.D 4.A 5.D 6.A 7.C 8.C
10.或（答出这两种形式中任意一种均得分）
11.
12.
13.3
14.的图象与x轴交于两点，
∴，
∵，
∴或．
15.解：（1）证明：∵矩形MEFN与矩形EBCF面积相等，
∴ME＝BE，AM＝GH．
∵四块矩形花圃的面积相等，即S矩形AMDND＝2S矩形MEFN，
∴AM＝2ME，
∴AE＝3BE；
（2）∵篱笆总长为100m，
∴2AB+GH+3BC＝100，
即，
∴
设BC的长度为xm，矩形区域ABCD的面积为ym2，
则，
∵，
∴，
解得，
∴．
16.（1）直线与抛物线的对称轴交于点D（2，﹣3），
故抛物线的对称轴为x＝2，即12b＝2，解得：b＝﹣4，
故抛物线的表达式为：y＝x2﹣4x；
（2）把y＝﹣3代入y＝x2﹣4x并解得x＝1或3，
故点B、C的坐标分别为（1，﹣3）、（3，﹣3），则BC＝2，
∵四边形PBCQ为平行四边形，
∴PQ＝BC＝2，故x2﹣x1＝2，
又∵y1＝x12﹣4x1，y2＝x22﹣4x2，|y1﹣y2|＝2，
故|（x12﹣4x1）﹣（x22﹣4x2）＝2，|x1+x2﹣4|＝1．
∴x1+x2＝5或x1+x2＝﹣3，
由x2−x1=2x1+x2=5，解得x1=32x2=72；
由x2−x1=2x1+x2=3，解得x1=12x2=52．