中考数学第一轮复习13 几何最值问题2种题型（将军饮马与蚂蚁爬行,16种模型）练习（解析版）

这是一份中考数学第一轮复习13 几何最值问题2种题型（将军饮马与蚂蚁爬行,16种模型）练习（解析版），共99页。
目 录
TOC \ "1-3" \n \h \z \u
\l "_Tc157755234" 题型01 将军饮马
\l "_Tc157755235" 题型02 蚂蚁爬行

题型01 将军饮马
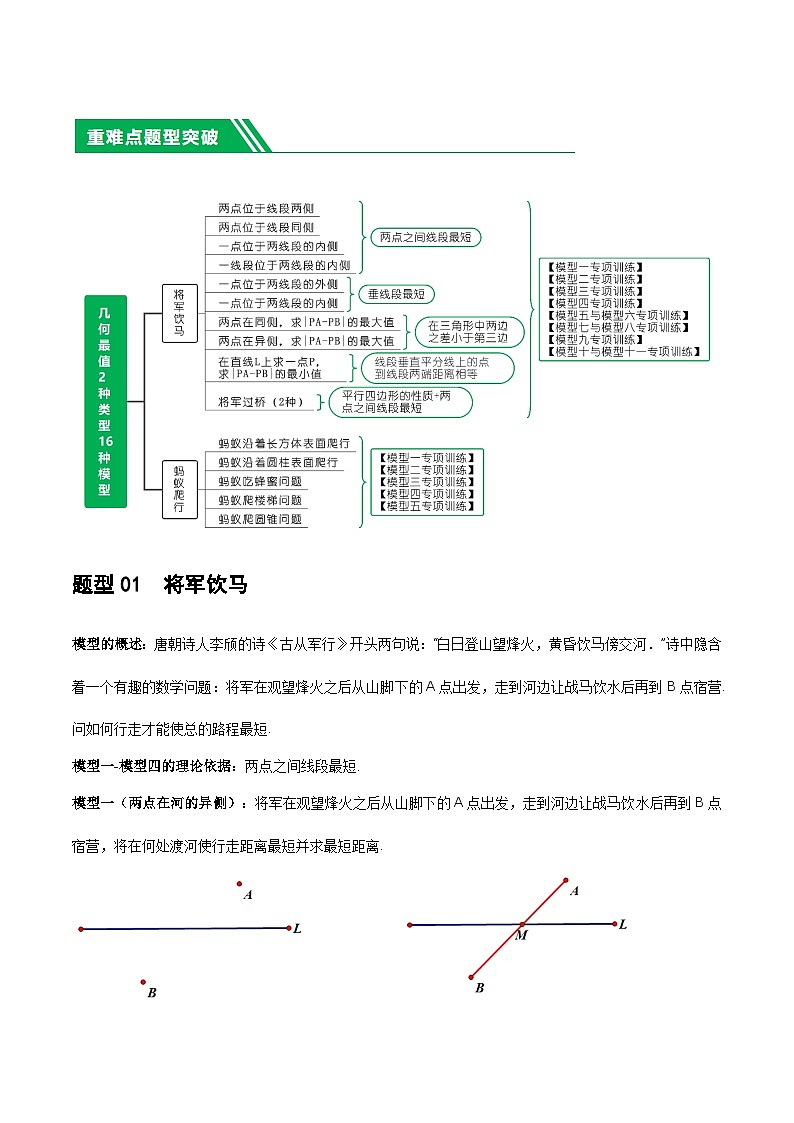
模型的概述：唐朝诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河．”诗中隐含着一个有趣的数学问题：将军在观望烽火之后从山脚下的A点出发，走到河边让战马饮水后再到B点宿营.问如何行走才能使总的路程最短.
模型一-模型四的理论依据：两点之间线段最短.
模型一（两点在河的异侧）：将军在观望烽火之后从山脚下的A点出发，走到河边让战马饮水后再到B点宿营，将在何处渡河使行走距离最短并求最短距离.

方法：如右图，连接AB，与线段L交于点M,在M处渡河距离最短，最短距离为线段AB的长.
【将军饮马之模型一 专项训练】
1．（2021·海南海口·统考一模）如图，在△ABC中，AB＝AC，分别以点A、B为圆心，以适当的长为半径作弧，两弧分别交于E，F，作直线EF，D为BC的中点，M为直线EF上任意一点．若BC＝4，△ABC面积为10，则BM+MD长度的最小值为（ ）
A．52B．3C．4D．5
【答案】D
【分析】由基本作图得到得EF垂直平分AB，则MB＝MA，所以BM+MD＝MA+MD，连接MA、DA，如图，利用两点之间线段最短可判断MA+MD的最小值为AD，再利用等腰三角形的性质得到AD⊥BC，然后利用三角形面积公式计算出AD即可．
【详解】解：由作法得EF垂直平分AB，
∴MB＝MA，
∴BM+MD＝MA+MD，
连接MA、DA，如图，
∵MA+MD≥AD（当且仅当M点在AD上时取等号），
∴MA+MD的最小值为AD，
∵AB＝AC，D点为BC的中点，
∴AD⊥BC，
∵S△ABC=12BC·AD=10,
∴AD=10×24=5,
∴BM+MD长度的最小值为5．
故选：D．
【点睛】本题考查的是线段的垂直平分线的性质，利用轴对称求线段和的最小值，三角形的面积，两点之间，线段最短，掌握以上知识是解题的关键．
2．（2023·山东枣庄·校考模拟预测）如图所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（ ）
A．43B．23C．6D．3
【答案】B
【分析】连接BD，PB，根据点B与D关于AC对称，得出PD=PB，从而得出PD+PE=PB+PE≥BE，即PD+PE最小值为值为BE的长，求出BE的长即可．
【详解】解：连接BD，PB，如图所示：
∵四边形ABCD为正方形，
∴点B与D关于AC对称，
∴PD=PB，
∴PD+PE=PB+PE≥BE，
∴PD+PE最小值为BE的长，
∵正方形ABCD的面积为12，
∴AB=12=23，
又∵△ABE是等边三角形，
∴BE=AB=23，
∴PD+PE最小值为23，故B正确．
故选：B．
【点睛】本题主要考查了正方形的性质，轴对称的性质，等边三角形的性质，解题的关键是根据轴对称的性质得出BE的长为PD+PE的最小值．
3．（2020·山东泰安·中考真题）如图，点A，B的坐标分别为A(2,0),B(0,2)，点C为坐标平面内一点，BC=1，点M为线段AC的中点，连接OM，则OM的最大值为（ ）

A．2+1B．2+12C．22+1D．22-12
【答案】B
【分析】如图所示，取AB的中点N，连接ON，MN，根据三角形的三边关系可知OM＜ON+MN，则当ON与MN共线时，OM= ON+MN最大，再根据等腰直角三角形的性质以及三角形的中位线即可解答．
【详解】解：如图所示，取AB的中点N，连接ON，MN，三角形的三边关系可知OM＜ON+MN，则当ON与MN共线时，OM= ON+MN最大，
∵A(2,0),B(0,2)，
则△ABO为等腰直角三角形，
∴AB=OA2+OB2=22，N为AB的中点，
∴ON=12AB=2，
又∵M为AC的中点，
∴MN为△ABC的中位线，BC=1，
则MN=12BC=12，
∴OM=ON+MN=2+12，
∴OM的最大值为2+12
故答案选：B．

【点睛】本题考查了等腰直角三角形的性质以及三角形中位线的性质，解题的关键是确定当ON与MN共线时，OM= ON+MN最大．
4．（2022·安徽蚌埠·统考一模）如图，Rt△ABC中，AB⊥BC，AB=8，BC=6，P是△ABC内部的一个动点，满足∠PAB=∠PBC，则线段CP长的最小值为（ ）
A．325B．2C．213-6D．213-4
【答案】D
【分析】结合题意推导得∠APB=90°，取AB的中点O，以点O为圆心，AB为直径作圆，连接OP；根据直角三角形斜边中线的性质，得OP=OA=OB=12AB=4；根据圆的对称性，得点P在以AB为直径的⊙O上，根据两点之间直线段最短的性质，得当点O、点P、点C三点共线时，PC最小；根据勾股定理的性质计算得OC，通过线段和差计算即可得到答案．
【详解】∵∠ABC=90°，
∴∠ABP+∠PBC=90°，
∵∠PAB=∠PBC，
∴∠BAP+∠ABP=90°，
∴∠APB=90°，
取AB的中点O，以点O为圆心，AB为直径作圆，连接OP，
∴OP=OA=OB=12AB=4
∴点P在以AB为直径的⊙O上，连接OC交⊙O于点P，
当点O、点P、点C三点共线时，PC最小
在Rt△BCO中，
∵∠OBC=90°，BC=6，OB=4，
∴OC=BO2+BC2=42+62=213，
∴PC=OC-OP=213-4
∴PC最小值为213-4
故选：D．
【点睛】本题考查了两点之间直线段最短、圆、勾股定理、直角三角形斜边中线的知识；解题的关键是熟练掌握圆的对称性、两点之间直线段最短、直角三角形斜边中线的性质，从而完成求解．
5．（2020·广东深圳·南山实验教育集团南海中学校考一模）如图，AC,BD在AB的同侧，AC=2,BD=8,AB=8，点M为AB的中点，若∠CMD=120∘，则CD的最大值是 ．
【答案】14
【分析】如图，作点A关于CM的对称点A′，点B关于DM的对称点B′，证明△A′MB′为等边三角形，即可解决问题．
【详解】解：如图，作点A关于CM的对称点A'，点B关于DM的对称点B'．
∵∠CMD=120∘，
∴∠AMC+∠DMB=60∘，
∴ ∠CMA'+∠DMB'=60∘，
∴∠A'MB'=60∘，
∵MA'=MB'，
∴ΔA'MB'为等边三角形
∵CD≤CA'+A'B'+B'D=CA+AM+BD=14，
∴CD的最大值为14，
故答案为14．
【点睛】本题考查等边三角形的判定和性质，两点之间线段最短，解题的关键是学会添加常用辅助线，学会利用两点之间线段最短解决最值问题
模型二（两点在河的同侧）：将军在观望烽火之后从山脚下的A点出发，需先走到河边让战马饮水后再到B点宿营，将在何处渡河使行走距离最短并求最短距离.

方法：如右图，作点B关于直线L的对称点B’，连接AB’,与直线L的交点即为所求的渡河点，最短距离为线段AB’的长.
【将军饮马之模型二 专项训练】
1．（2022·湖南湘潭·校考模拟预测）如图，菱形草地ABCD中，沿对角线修建60米和80米两条道路AC1)，现计划在河岸l上建一抽水站P，用输水管向两个村庄供水．如何铺设使得管道长度较短？
方案设计：某班数学兴趣小组设计了两种铺设管道方案：图1是方案一的示意图，设该方案中管道长度为d1，且d1=PB+BA(km)（其中BP⊥l于点P）；图2是方案二的示意咨图，设该方案中管道长度为d2，且d2=PA+PB(km)（其中点A'与点A关于l对称，A'B与l交于点P）．
(1)在方案一中，d1=______km（用含a的式子表示）；
(2)在方案二中，组长小宇为了计算d2的长，作了如图3所示的辅助线，请你按小宇同学的思路计算，d2=_______km（用含a的式子表示）．
(3)①当a=4时，比较大小：d1_______d2（填“＞”、“＝”或“＜”）；
②当a=7时，比较大小：d1______d2（填“＞”、“＝”或“＜”）；
(4)请你参考方框中的方法指导，就a（当a>1时）的所有取值情况进行分析，要使铺设的管道长度较短，应选择方案还是方案二？
【答案】(1)a+3
(2)a2+48
(3)①＜；②＞
(4)见解析
【分析】（1）由题意可以得知管道长度为d1=PB+BA（km），根据BP⊥l于点P得出PB=3，故可以得出d1的值为a+3．
（2）由条件根据勾股定理可以求出KB的值，由轴对称可以求出A′K的值，在Rt△KBA′由勾股定理可以求出A′B的值a2+48就是管道长度．
（3）①把a=4代入d1=a+3和d2=a2+48就可以比较其大小；
②把a=7代入d1=a+3和d2=a2+48就可以比较其大小；
（4）分类进行讨论当d1＞d2，d1=d2，d1＜d2时就可以分别求出a的范围，从而确定选择方案．
【详解】（1）解：∵如图1， 由题意得：d1=PB+BA=a+3；
故答案为：a+3；
（2）因为BK2=a2-1，
A'B2=BK2+A'K2=a2-1+72=a2+48，
所以d2=a2+48，
故答案为：a2+48；
（3）①当a=4时，d1=7，d2=8，d1＜d2；
②当a=7时，d1=10，d2=97，d1＞d2；
故答案为：＜，＞；
（4）d12-d22=（a+3）2-（a2+48）2=6a-39．
①当6a-39＞0，即a＞132时，d12-d22＞0，
∴d1-d2＞0，
∴d1＞d2；
②当6a-39=0，即a=132时，d12-d22=0，
∴d1-d2=0，
∴d1=d2；
③当6a-39＜0，即a＜132时，d12-d22＜0，
∴d1-d2＜0，
∴d1＜d2
综上可知：当a＞132时，选方案二；
当a=132时，选方案一或方案二；
当1＜a＜132时，选方案一．
【点睛】本题考查了轴对称的性质的运用，最短路线问题数学模式的运用，勾股定理的运用，数的大小的比较方法的运用，综合考查了学生的作图能力，运用数学知识解决实际问题的能力，以及观察探究和分类讨论的数学思想方法．
模型三：如图，将军同部队行驶至P处，准备在此驻扎，但有哨兵发现前方为两河AB、BC的交汇处，为防止敌军在对岸埋伏需派侦察兵到河边观察，再返回P处向将军汇报情况，问侦察兵在AB、BC何处侦查才能最快完成任务并求最短距离.
数学描述：如图在直线AB、BC上分别找点M、N，使得∆PMN周长最小.
方法：如右图，分别作点P关于直线AB、BC的对称点P’、P’’，连接P’ P’’，与两直线的交点即为所求点M、N，最短距离为线段P’ P’’的长.
【将军饮马之模型三 专项训练】
1．（2020·全国·九年级专题练习）如图，在四边形ABCD中，∠B=∠D=90°，E，F分别是BC，CD上的点，连接AE，AF，EF．
（1）如图①，AB=AD，∠BAD=120°，∠EAF=60°．求证：EF=BE+DF；

（2）如图②，∠BAD=120°，当△AEF周长最小时，求∠AEF+∠AFE的度数；
（3）如图③，若四边形ABCD为正方形，点E、F分别在边BC、CD上，且∠EAF=45°，若BE=3，DF=2，请求出线段EF的长度．
【答案】（1）见解析；（2）∠AEF+∠AFE =120°；（3）EF=5．
【分析】（1）延长FD到点G,使DG=BE，连接AG，首先证明△ABE≌△ADG，则有AE=AG，∠BAE=∠DAG，然后利用角度之间的关系得出∠EAF=∠FAG=60°，进而可证明△EAF≌△GAF，则EF=FG=DG+DF，则结论可证；
（2）分别作点A关于BC和CD的对称点A'，A″，连接A'A″，交BC于点E，交CD于点F，根据轴对称的性质有A'E=AE，A″F=AF，当点A'、E、F、A″在同一条直线上时，A'A″即为△AEF周长的最小值，然后利用∠AEF+∠AFE=∠EA'A+∠EAA'+∠FAD+∠A″求解即可；
（3）旋转△ABE至△ADP的位置，首先证明△PAF≌△EAF，则有EF=FP，最后利用EF=PF=PD+DF=BE+DF求解即可．
【详解】（1）证明：如解图①，延长FD到点G，使DG=BE，连接AG，
在△ABE和△ADG中，
AB=AD,∠ABE=∠ADG,BE=DG,
∴△ABE≌△ADGSAS．
∴AE=AG，∠BAE=∠DAG，
∵∠BAD=120°，∠EAF=60°，
∴∠BAE+∠FAD=∠DAG+∠FAD=60°．
∴∠EAF=∠FAG=60°，
在△EAF和△GAF中，
AE=AG,∠EAF=∠GAF,AF=AF,
∴△EAF≌△GAFSAS．
∴EF=FG=DG+DF，∴EF=BE+DF；
（2）解：如解图，分别作点A关于BC和CD的对称点A'，A″，连接A'A″，交BC于点E，交CD于点F．
由对称的性质可得A'E=AE，A″F=AF，
∴此时△AEF的周长为AE+EF+AF=A'E+EF+A'F=A'A″．
∴当点A'、E、F、A″在同一条直线上时，A'A″即为△AEF周长的最小值．
∵∠DAB=120°，
∴∠AA'E+∠A″=180°-120°=60°．
∵∠EA'A=∠EAA',∠FAD=∠A″，∠EA'A+∠EAA'=∠AEF,∠FAD+∠A″=∠AFE，
∴∠AEF+∠AFE=∠EA'A+∠EAA'+∠FAD+∠A″= 2∠AA'E+∠A″=2×60°=120°；
（3）解：如解图，旋转△ABE至△ADP的位置，
∴∠PAE=∠DAE+∠PAD=∠DAE+∠EAB=90°，
AP=AE，∠PAF=∠PAE-∠EAF =90°-45°=45°=∠EAF．
在△PAF和△EAF中，
AP=AE,∠PAF=∠EAF,AF=AF,
∴△PAF≌△EAFSAS．
∴EF=FP．
∴EF=PF=PD+DF=BE+DF=3+2=5．
【点睛】本题主要考查全等三角形的判定及性质，轴对称的性质，掌握全等三角形的判定及性质是解题的关键．
2．（2019下·河南南阳·七年级统考期末）（1）【问题解决】已知点P在∠AOB内，过点P分别作关于OA、OB的对称点P1、P2.
①如图1，若∠AOB=25∘，请直接写出∠P1OP2=______；
②如图2，连接P1P2分别交OA、OB于C、D，若∠CPD=98∘，求∠AOB的度数；
③在②的条件下，若∠CPD=α度（90y2>0，求自变量x的取值范围；
(2)动点Pn,0在x轴上运动．当n为何值时，PA-PC的值最大？并求最大值．
【答案】(1)x>1
(2)当n为-2时，|PA-PC|的值最大，最大值为2
【分析】（1）由点A的纵坐标利用反比例函数图象上点的坐标特征即可求出点A的坐标，再根据两函数图象的上下位置关系，即可得出当y1>y2>0时，自变量x的取值范围；
（2）由点A的坐标利用待定系数法即可求出直线AB的函数解析式，利用一次函数图象上点的坐标特征可求出点B、C的坐标，再根据三角形的三边关系即可确定当点P与点B重合时，|PA-PC|的值最大，利用两点间的距离公式即可求出此最大值．
【详解】（1）解：当y2=3x=3时，x=1，
∴点A的坐标为(1,3)，
观察函数图象，可知：当x>1时，直线在双曲线上方，
∴若y1>y2>0，自变量x的取值范围为x>1．
（2）解：将A(1,3)代入y1=kx+2中，
3=k+2，解得：k=1，
∴直线AB的解析式为y1=x+2，
当x=0时，y1=x+2=2，
∴点C的坐标为(0,2)，
∴AC=(0-1)2+(2-3)2=2，
当y1=x+2=0时，x=-2，
∴点B的坐标为(-2,0)．
当点P与点B重合时，|PA-PC|的值最大，
此时n=-2，|PA-PC|=AC=2．
∴当n为-2时，|PA-PC|的值最大，最大值为2．
【点睛】本题考查了反比例函数与一次函数的交点问题、一次（反比例）函数图象上点的坐标特征、待定系数法求一次函数解析式以及三角形的三边关系，解题的关键是：（1）利用反比例函数图象上点的坐标特征求出点A的坐标；（2）利用三角形的三边关系确定点P的位置．
3．（2023·贵州遵义·统考一模）如图，二次函数y=ax2-2ax+c的图象与x轴交于A、B3,0两点，与y轴相交于点C0,-3．
(1)求二次函数的解析式；
(2)若点P是对称轴上一动点，当PB-PC有最大值时，求点P的坐标．
【答案】(1)y=x2-2x-3
(2)1,-6
【分析】（1）把点B、C的坐标分别代入解析式，解方程组，即可求解；
（2）连接PA，则PA=PB，根据三角形三边的关系得PB-PC=PA-PC≤AC (当点A、C、P共线时取等号)，延长AC交直线x=1于点P'，即P'点为所求，再利用待定系数法求出直线AC的解析式，从而可得P'点坐标．
【详解】（1）解：点B、C的坐标分别代入解析式，得
9a-6a+c=0c=-3
解得a=1c=-3
故二次函数的解析式为y=x2-2x-3；
（2）解：y=x2-2x-3=x-12-4，
故该二次函数图象的对称轴为直线x=1，
∵B3,0，
∴A-1,0，
如图，连接PA，则PA=PB，
∴PB-PC=PA-PC≤AC (当点A、C、P共线时取等号)，
延长AC交直线x=1于点P'，
设直线AC的解析式为y=mx+n，
把A-1,0，C0,-3代入得：
-m+n=0n=-3
解得m=-3n=-3，
∴直线AC的解析式为y=-3x-3，
当x=1时，y=-3x-3=-6，即P'1,-6，
∴当PB-PC达到最大值时，点P的坐标为1,-6．
【点睛】本题考查了利用待定系数法求一次函数及二次函数的解析式，抛物线与x轴的交点，利用轴对称和三角形三边的关系解决最短路径问题，找到点P'的位置是解决本题的关键．
4．（2020·广东东莞·东莞市长安培英初级中学校考二模）如图，点A（－2，n），B（1，－2）是一次函数y＝kx＋b的图象和反比例函数y＝mx的图象的两个交点．
（1）求反比例函数和一次函数的解析式；
（2）根据图象写出，当kx＋bAC，
∴AN+BN>AC，
当点D与点M重合时，AN+BN=AB=AC，

∴△ABC周长=AN+CN+AC+BC≥2AC+BC，
∴△ABC周长的最小值=2AC+BC，
∵∠BAC=60°，AB=AC
∴△ABC为等边三角形，
∵AD为BC边上的高，AD=4，
∴AB=ADsin∠B=4sin60°=833，
∴△ABC周长的最小值=3×833=83，
故答案为：83．
【点睛】本题主要考查了等边三角形的判定和性质，解直角三角形，解题的关键是正确作出辅助线，确定当△ABC周长最小时的情况．
模型十：如图，一条宽度相同的河流两侧有A、B两个营地，将军令下属在河流间搭建一座垂直于河岸的桥梁MN，使得AM+MN+NB之和最短，在何处搭建桥梁才能完成任务呢？
方法：如右图，将点A向下平移MN的单位长度得到点A’，连接A’B，交n于点N，过点N作MN⊥m，垂足为点M，点M和点N即为所求，最短距离为A’B+MN
模型十一：线段MN在直线L上可移动，且MN=a，当MN移动到什么位置时，求AM+MN+NB最小值.
方法：如右图，将点A向右平移a个单位长度得点A’，作B关于直线L的对称点B’，连接A’B’，交直线L于点N，将点N向左平移a个单位长度得点M，点M和点N即为所求，最短距离为A’B’+MN
模型十、十一的理论依据：平行四边形的性质+两点之间线段最短.
【将军饮马之模型十与模型十一 专项训练】
1．（2023·江苏盐城·统考三模）如图，在▱ABCD中，AB=4，AD=9，M、N分别是AD、BC边上的动点，且∠ABC=∠MNB=60°，则BM+MN+ND的最小值是 ．

【答案】129+4/4+129
【分析】由∠MNB=60°可知MN为定长，在AD、BC间滑动，故由造桥选址模型进行平移，转化为两点间距离加上定长，再利用特殊角构造直角三角形，使用勾股定理求出两点间距离．
【详解】解：作ME∥AB交BC于点E，在AD取DF=MN，连接EF，延长AB至点B'，使BB'=ME，连接B'F，作B'H⊥AD于点H，如下图：

∵AB∥ME，
∴∠MEN=∠ABC=∠MNB=60°，
∴△MEN为等边三角形，
∴ME=EN=MN，
∵▱ABCD，
∴AD∥BC，
∴四边形ABEM为平行四边形，
同理得四边形BB'EM与四边形ENDF为平行四边形，
∴ME=EN=MN=AB=4，B'E=BM，EF=ND，
∴BM+MN+ND=B'E+EN+ND=B'E+EF+4≥B'F+4，
Rt△B'HA中，HA=12B'A=4，B'H=B'A2-AH2=82-42=43，
Rt△B'HF中，B'F=B'H2+HF2=B'H2+AH+AD-FD2=B'H2+AD2=432+92=129，
∴BM+MN+ND≥129+4，
即BM+MN+ND的最小值是129+4．
故答案为：129+4．
【点睛】本题考查平移类最短路径，为造桥选址模型，即沿一个方向平移的定长线段两端到两个定点距离和最小，解题的关键是需要理清楚是否含有定长平移线段，且利用平移求出最短路径位置．
2．（2023·陕西西安·校考模拟预测）如图，▱ABCD中，AB=3，AD=2，∠DAB=60°，DF⊥AB，BE⊥CD；垂足分别为点F和E．点G和H分别是DF和BE上的动点，GH∥AB，那么AG+GH+CH的最小值为 ．

【答案】7+2/2+7
【分析】过点E作EI∥AD交AB于点I，连接HI．易求出AF=1，DF=3，DE=GH=BF=2．易证四边形AGHI为平行四边形，得出AG=HI，即说明当HI+CH最小时，AG+GH+CH最小．由当点I，H，C三点共线时，HI+CH最小．结合平行四边形的判定和性质和勾股定理求出HI=72，即得出CI=7，即可得出答案．
【详解】解：如图，过点E作EI∥AD交AB于点I，连接HI．

∵▱ABCD中，∠DAB=60°，DF⊥AB，
∴∠ADF=30°，
∴AF=12AD=1，
∴BF=AB-AF=2，DF=AD2-AF2=3．
∵DF⊥AB，BE⊥CD，
∴GF∥BH．
∵GH∥AB，
∴四边形GHBF为平行四边形，
∴GH=BF=2．
同理可得出BF=DE=2．
∵AB∥DE，AD∥EI，
∴四边形ADEI为平行四边形，
∴AI=DE=2=GH，
∴四边形AGHI为平行四边形，
∴AG=HI，
∴AG+GH+CH=HI+2+CH，
∴当HI+CH最小时，AG+GH+CH最小．
∵当点I，H，C三点共线时，HI+CH最小，
∴此时AG+GH+CH最小，如图，

∵AD∥EI，
∴BC∥EI．
∵CE∥BI，
∴四边形BCEI为平行四边形，
∴BH=12BE=12DF=32，CI=2HI，
∵AB=3，AI=2，
∴BI=1，
∴HI=BH2+BI2=72，
∴CI=7，
∴AG+GH+CH的最小值为CI+GH=7+2．
故答案为：7+2．
【点睛】本题考查平行四边形的性质和判定，含30度角的直角三角形，勾股定理，平行线的判定，两点之间线段最短等知识．正确作出辅助线，理解当点I，H，C三点共线时，HI+CH最小，即此时AG+GH+CH最小是解题关键．
3（2022上·广东广州·八年级统考期末）在长方形ABCD中，AB＝4，BC＝8，点P、Q为BC边上的两个动点（点P位于点Q的左侧，P、Q均不与顶点重合），PQ＝2
(1)如图①，若点E为CD边上的中点，当Q移动到BC边上的中点时，求证：AP＝QE；
(2)如图②，若点E为CD边上的中点，在PQ的移动过程中，若四边形APQE的周长最小时，求BP的长；
(3)如图③，若M、N分别为AD边和CD边上的两个动点（M、N均不与顶点重合），当BP＝3，且四边形PQNM的周长最小时，求此时四边形PQNM的面积．
【答案】(1)见解析
(2)4
(3)4
【分析】（1）由“SAS”可证△ABP≌△QCE，可得AP=QE；
（2）要使四边形APQE的周长最小，由于AE与PQ都是定值，只需AP+EQ的值最小即可．为此，先在BC边上确定点P、Q的位置，可在AD上截取线段AF=DE=2，作F点关于BC的对称点G，连接EG与BC交于一点即为Q点，过A点作FQ的平行线交BC于一点，即为P点，则此时AP+EQ=EG最小，然后过G点作BC的平行线交DC的延长线于H点，那么先证明∠GEH=45°，再由CQ=EC即可求出BP的长度；
（3）要使四边形PQNM的周长最小，由于PQ是定值，只需PM+MN+QN的值最小即可，作点P关于AD的对称点F，作点Q关于CD的对称点H，连接FH，交AD于M，交CD于N，连接PM，QN，此时四边形PQNM的周长最小，由面积和差关系可求解．
【详解】（1）解：证明：∵四边形ABCD是矩形，
∴CD=AB=4，BC=AD=8，
∵点E是CD的中点，点Q是BC的中点，
∴BQ=CQ=4，CE=2，
∴AB=CQ，
∵PQ=2，
∴BP=2，
∴BP=CE，
又∵∠B=∠C=90°，
∴△ABP≌△QCE（SAS），
∴AP=QE；
（2）如图②，在AD上截取线段AF=PQ=2，作F点关于BC的对称点G，连接EG与BC交于一点即为Q点，过A点作FQ的平行线交BC于一点，即为P点，过G点作BC的平行线交DC的延长线于H点．
∵GH=DF=6，EH=2+4=6，∠H=90°，
∴∠GEH=45°，
∴∠CEQ=45°，
设BP=x，则CQ=BC-BP-PQ=8-x-2=6-x，
在△CQE中，∵∠QCE=90°，∠CEQ=45°，
∴CQ=EC，
∴6-x=2，
解得x=4，
∴BP=4；
（3）如图③，作点P关于AD的对称点F，作点Q关于CD的对称点H，连接FH，交AD于M，交CD于N，连接PM，QN，此时四边形PQNM的周长最小，连接FP交AD于T，
∴PT=FT=4，QC=BC-BP-PQ=8-3-2=3=CH，
∴PF=8，PH=8，
∴PF=PH，
又∵∠FPH=90°，
∴∠F=∠H=45°，
∵PF⊥AD，CD⊥QH，
∴∠F=∠TMF=45°，∠H=∠CNH=45°，
∴FT=TM=4，CN=CH=3，
∴四边形PQNM的面积=12×PF×PH-12×PF×TM-12×QH×CN=12×8×8-12×8×4-12×6×3=7．
【点睛】本题是四边形综合题，考查了矩形的性质，全等三角形的判定和性质，轴对称求最短距离，直角三角形的性质；通过构造平行四边形和轴对称找到点P和点Q位置是解题的关键．
4．（2022·全国·九年级专题练习）在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，A（3，0），B（0，4），D为边OB的中点.
(1)若E为边OA上的一个动点，求△CDE的周长最小值；
(2)若E、F为边OA上的两个动点，且EF=1，当四边形CDEF的周长最小时，求点E、F的坐标.
【答案】(1)13+35
(2)23,0，53,0
【分析】（1）作点D关于x轴的对称点D'，连接CD'与x轴交于点E，连接DE，先求出直线CD'的关系式，得出点E的坐标，求出AE=2，根据勾股定理求出CD=13，DE=5，CE=25，即可得出答案；
（2）将点D向右平移1个单位得到D'（1,2），作D'关于x轴的对称点D″（1,-2），连接CD″交x轴于点F，将点F向左平移1个单位到点E，此时点E和点F为所求作的点，用待定系数法求出CD″的关系式，然后求出与x轴的交点坐标，即可得出答案．
【详解】（1）解：如图，作点D关于x轴的对称点D'，连接CD'与x轴交于点E，连接DE，由模型可知△CDE的周长最小，
∵在矩形OACB中，OA=3，OB=4，D为OB的中点，
∴D（0，2），C（3，4），D'（0，-2），
设直线CD'为y=kx＋b，把C（3，4），D'（0，-2）代入，
得3k＋b=4，b=-2，解得k=2，b=-2，
∴直线CD'为y=2x-2，
令y=0，得x=1，
∴点E的坐标为（1，0）.
∴OE=1，AE=2，
利用勾股定理得CD=32+22=13，
DE=12+22=5，
CE=22+42=25，
∴△CDE周长的最小值为：13+5+25=13+35．
（2）解：如图，将点D向右平移1个单位得到D'（1,2），作D'关于x轴的对称点D″（1,-2），连接CD″交x轴于点F，将点F向左平移1个单位到点E，此时点E和点F为所求作的点，连接D″F，此时四边形CDEF周长最小，
理由如下：
∵四边形CDEF的周长为CD＋DE＋EF＋CF，CD与EF是定值，
∴DE＋CF最小时，四边形CDEF周长最小，
∵DD'∥EF，且DD'=EF，
∴四边形DD'FE为平行四边形，
∴DE=D'F，
根据轴对称可知，D'F=D″F，
∴DE＋CF=D'F＋CF=FD″＋CF=CD″，
设直线CD″的解析式为y=kx＋b，把C（3，4），D″（1,-2）代入，
得3k＋b=4k＋b=-2，解得k=3b=-5，
∴直线CD″的解析式为y=3x-5，
令y=0，得x=53，
∴点F坐标为53,0，
∴点E坐标为23,0．
【点睛】本题主要考查了轴对称的性质，将军饮马问题，根据题意作出辅助线，找出最短时动点的位置，是解题的关键．
5（2023·陕西西安·西安市庆安初级中学校联考模拟预测）在▱ABCD中，AB⊥AC，点E在边AD上，连接BE．

(1)如图1，AC交BE于点G，GH⊥AE，若BE平分∠ABC，且∠DAC=30°，CG=4，请求出四边形EGCD的面积；
(2)如图2，点F在对角线AC上，且AF=AB，连接BF，过点F作FH⊥BE于点H，连接AH，求证：HF+2AH=BH；
(3)如图3，线段PQ在线段BE上运动，点R在BC上，连接CQ，PR．若BE平分∠ABC，∠DAC=30°，AB=3，AC=BE=2PQ=3，BC=4BR．求线段CQ+PQ+PR的和的最小值．
【答案】(1)53
(2)见解析
(3)21+32
【分析】（1）由▱ABCD得到∠ABC=60°，根据角平分线求出∠ABE=∠CBE=30°，且∠ACB=∠DAC=30°，得到CG=BG=4，利用30度角的性质得到AG=EG=2．再求出CD,AH,GH，即可根据SΔEGCD=SΔACD-SΔAGE求出答案；
（2）过点A作AJ⊥AH于点A，交FH的延长线于点J．得∠BAF=∠BHF=∠BHJ=90°，∠AFB=∠ABF=45°，推出点A，B，F，H四点共圆，证得△AHJ是等腰直角三角形，得到AH=AJ，进而证得△ABH≌△AFJSAS，推出BH=FJ，由此得到结论FJ=HF+JH=HF+2AH即可．
（3）取AB的中点M，AE的中点N，连接PM，NQ，MN，则MN∥BE，MN=12BE=32．证得四边形PMNQ是平行四边形，得PM=NQ．在Rt△ABC中，BC=2AB，得BC=4BM推出BM=BR．证明△PBM≌△PBRSAS，得到PR=PM，由此得到CQ+PQ+PR的最小值为CN+32．过点C作CS⊥AD于点S．利用勾股定理求出CN即可．
【详解】（1）解：在▱ABCD中，∠BAC=90°，∠DAC=30°，
∴∠ABC=60°．
∵BE平分∠ABC，
∴∠ABE=∠CBE=30°，且∠ACB=∠DAC=30°，
∴CG=BG=4
∵∠ABE=∠AEB=30°，
∴AG=EG=2．
∵∠DAC=30°，
∴CD=2+4×33=23，AH=2×32=3，GH=2×12=1．
∴SΔEGCD=SΔACD-SΔAGE=12×2+4×23-12×1×3×2=63-3=53；
（2）证明：如图1，过点A作AJ⊥AH于点A，交FH的延长线于点J．

∵FH⊥BE，AB⊥AC，AB=AF，
∴∠BAF=∠BHF=∠BHJ=90°，∠AFB=∠ABF=45°，
∴点A，B，F，H四点共圆，
∴∠BHA=∠AFB=45°，
∴∠AHJ=45°，
∴△AHJ是等腰直角三角形，
∴AH=AJ，
∴JH=2AH．
∵AB=AF，∠BAH=∠FAJ=90°+∠OAH，AH=AJ，
∴△ABH≌△AFJSAS，
∴BH=FJ．
∵FJ=HF+JH=HF+2AH．
∴BH=FJ=HF+2AH；
（3）解：如图2，取AB的中点M，AE的中点N，连接PM，NQ，MN，则MN∥BE，MN=12BE=32．
由题意，得PQ=12BE=32，
∴PQ∥MN，PQ=MN，
∴四边形PMNQ是平行四边形，
∴PM=NQ．
在▱ABCD中，∠DAC=30°，
∴∠ACB=30°．
在Rt△ABC中，BC=2AB．
∵点M为AB的中点，
∴BC=4BM．
∵BC=4BR，
∴BM=BR．
∵BE平分∠ABC，
∴∠PBM=∠PBR．
∵BP=BP，
∴△PBM≌△PBRSAS，
∴PR=PM，
∴NQ=PR，
∴CQ+PQ+PR=CQ+NQ+32．
∵CQ+NQ≥CN，
∴CQ+PQ+PR的最小值为CN+32．
如图2，过点C作CS⊥AD于点S．

由（1），得∠ABE=∠AEB=30°，
∴AE=AB=3，
∴AM=AN=12AE=32．
∵∠DAC=30°，
∴AD=2CD=23，CS=12AC=32，
∴SD=CD2-CS2=32，
∴NS=AD-AN-SD=3，
∴CN=CS2+NS2=212，
∴CQ+PQ+PR的最小值为212+32=21+32．
【点睛】此题考查了平行四边形的性质，全等三角形的判定和性质，直角三角形30度角的性质，勾股定理，综合掌握各图形的判定和性质是解题的关键．
题型02 蚂蚁爬行
蚂蚁爬行模型的概述：蚂蚁在某几何体的一个顶点，爬行到另外一个相对的顶点去吃食物，求所走的最短路径是多少。
蚂蚁爬行模型的实质：两点之间，线段最短。
模型一：蚂蚁沿着长方体表面爬行，从点A到点B的最短距离：
解题方法：在长方体问题中，我们需要将长方体展开，然后利用两点之间线段最短画图求解。如果长方体的长、宽、高各不相同，一般分三种情况讨论。
【蚂蚁爬行之模型一 专项训练】
1．（2023·江苏常州·校考一模）如图，是一个棱长为1的正方体纸盒，若一只蚂蚁要沿着正方体纸盒的表面，从顶点A爬到顶点B去觅食，则需要爬行的最短路程是（ ）
A．3B．2C．5D．3
【答案】C
【分析】根据正方体展开图的特点，将正方体展开，然后利用勾股定理求解即可．
【详解】解：如图所示，将正方体展开，则AC=2，BC=1，∠ACB=90°，
∴由勾股定理得AB=AC2+BC2=5，
∴需要爬行的最短路程是5，
故选C．
【点睛】本题主要考查了勾股定理的实际应用，正确将正方体展开，利用勾股定理进行求解是解题的关键．
2．（2020·陕西西安·校考模拟预测）如图，长方体的长EF为3cm，宽AE为2cm，高CE为4cm，B是GF的中点，一只蚂蚁如果要沿着长方体的表面从点D爬到点B，那么它需要爬行的最短距离是（ ）
A．5cmB．29cmC．(22+3)cmD．(2+13)cm
【答案】B
【分析】若要求蚂蚁爬行的最短距离，需将长方体的侧面展开，进而根据“两点之间线段最短”得出结果．
【详解】解：（1）如图展开时，
CD=2cm，GF=4cm，CG=3cm，
∵B是GF的中点，
∴GB=2cm，∴CB=5cm，
∴DB=22+52=29cm，
（2）如图展开时，
CD=2cm，GF=4cm，CG=3cm，GB=2cm，
∴DG=5cm，
∴DB=22+52=29cm
故选：B．
【点睛】本题是一道趣味题，将长方体展开，根据两点之间线段最短，运用勾股定理解答即可．
3．（2020·内蒙古呼伦贝尔·统考二模）如图，正方体的棱长为2，B为一条棱的中点．已知蚂蚁沿正方体的表面从A点出发，到达B点，则它运动路程最短时，CD的长是（ ）

A．1B．12C．13D．14
【答案】B
【分析】根据正方体的性质可得CD∥EB，AC=EC，即C为AE中点，推出CD是△ABE的中位线，根据正方体的边长为2，B为一条棱的中点，得出EB=1，即可得出CD．
【详解】解：画出展开图如下，

由正方体的性质可得CD∥EB，AC=EC，即C为AE中点，
∴CD是△ABE的中位线，
∴CD=12EB，
∵正方体的边长为2，B为一条棱的中点，
∴EB=1，
∴CD=12，
故选：B．
【点睛】本题考查了中位线的性质，正方体的性质，得出CD是△ABE的中位线是解题关键．
4．（2014·全国·九年级统考专题练习）如图，长方体的长为15，宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是（ ）

A．521B．25C．105+5D．35
【答案】B
【分析】要求长方体中两点之间的最短路径，最直接的作法，就是将长方体侧面展开，然后利用两点之间线段最短解答．
【详解】解：只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形，如图1，

∵长方体的宽为10，高为20，点B离点C的距离是5，
∴BD=CD+BC=10+5=15，AD=20，
在直角三角形ABD中，根据勾股定理得：AB=BD2+AD2=25；
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形，如图2，

∵长方体的宽为10，高为20，点B离点C的距离是5，
∴BD=CD+BC=20+5=25，
在直角三角形ABD中，根据勾股定理得：
∴AB=BD2+AD2=529；
只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形，如图3，

∵长方体的宽为10，高为20，点B离点C的距离是5，
∴AC=CD+AD=20+10=30，
在直角三角形ABC中，根据勾股定理得：
∴AB=AC2+BC2=537；
∵2541，
∴最短路径为41；
（3）如图1：
设AB=x，则BC′=9-x，
在Rt△ABC′中，由勾股定理得：
d=x2+（9-x）2，
d=2（x-92）2+812，
令y=2(x-92)2+812，
∵a=2>0且012
(2)20.7
【分析】（1）根据等腰直角三角形的性质和等腰三角形的性质进行计算即可；
（2）先根据圆锥的侧面展开图的知识和扇形的弧长公式计算，可求扇形的圆心角；再根据TA的定义即可解答．
【详解】（1）解：如图1，
∠A=90°，AB=AC，则BCAB=2，
∴F(90°)=ABBC=22，
如图2，
∠A=120°，AB=AC，作AD⊥BC于D，则∠BAD=60°，
∴BD=32AB，
∴BC=3AB，
∴T(120°)=ABBC=33；
∵2AB＞BC，
∴ABBC>12，
∴T（A）＞12．
故答案为：22;33;T(A)>12．
（2）解：∵圆锥的底面直径PQ=14，
∴圆锥的底面周长为14π，即侧面展开图扇形的弧长为14π，
设扇形的圆心角为n°，
则n⋅π×18180=14π，解得n＝140，
∵T70°≈0.87，
∴蚂蚁爬行的最短路径长为180.87≈20.7．
【点睛】本题主要考查了等腰直角三角形的性质、等腰三角形的性质、圆锥的侧面展开图、弧长公式等知识点，掌握相关性质定理和TA的定义是解本题的关键．
6．（2020·广东·统考一模）已知圆锥的底面半径为r＝20cm，高h=2015cm,现在有一只蚂蚁从底边上一点A出发．在侧面上爬行一周又回到A点，求蚂蚁爬行的最短距离．

【答案】802cm
【分析】蚂蚁爬行的最短距离是圆锥的展开图的扇形中AA′的长度．根据勾股定理求得母线长后，利用弧长等于底面周长求得扇形的圆心角的度数为90度，再由等腰直角三角形的性质求解．
【详解】解：设扇形的圆心角为n，圆锥的
在Rt△AOS中，∵r=20cm，h=2015cm，
∴由勾股定理可得母线l=r2+h2=80cm，
而圆锥侧面展开后的扇形的弧长为2×20π=nπ×80180.
∴n=90°
即△SAA′是等腰直角三角形，
∴由勾股定理得：AA'=802+802=802cm．
∴蚂蚁爬行的最短距离为802cm．
【点睛】本题利用了勾股定理，弧长公式，圆的周长公式，等腰直角三角形的性质求解．
7．（2022·广东潮州·校考一模）在几何体表面上，蚂蚁怎样爬行路径最短？
（1）如图①，圆锥的母线长为12cm，B为母线OC的中点，点A在底面圆周上，AC的长为4πcm．在图②所示的圆锥的侧面展开图中画出蚂蚁从点A爬行到点B的最短路径，并标出它的长（结果保留根号）．
（2）图③中的几何体由底面半径相同的圆锥和圆柱组成．O是圆锥的顶点，点A在圆柱的底面圆周上．设圆锥的母线长为l，圆柱的高为h．
①蚂蚁从点A爬行到点O的最短路径的长为________（用含l，h的代数式表示）．
②设AD的长为a，点B在母线OC上，OB=b．圆柱的侧面展开图如图④所示，在图中画出蚂蚁从点A爬行到点B的最短路径的示意图，并写出求最短路径的长的思路．
【答案】（1）作图如图所示；（2）①h +l；②见解析．
【分析】（1）根据两点之间线段最短，即可得到最短路径；连接OA，AC，可以利用弧长与母线长求出∠AOC，进而证明出△OAC是等边三角形，利用三角函数即可求解；
（2）①由于圆锥底面圆周上的任意一点到圆锥顶点的距离都等于母线长，因此只要蚂蚁从点A爬到圆锥底面圆周上的路径最短即可，因此顺着圆柱侧面的高爬行，所以得出最短路径长即为圆柱的高h加上圆锥的母线长l；
②如图，根据已知条件，设出线段GC的长后，即可用它分别表示出OE、BE、GE、AF，进一步可以表示出BG、GA，根据B、G、A三点共线，在Rt△ABH中利用勾股定理建立方程即可求出GC的长，最后依次代入前面线段表达式中即可求出最短路径长．
【详解】解：（1）如图所示，线段AB即为蚂蚁从点A爬行到点B的最短路径；
设∠AOC=n°，
∵圆锥的母线长为12cm， AC的长为4πcm，
∴12πn180=4π，
∴n=60；
连接OA、CA，
∵OA=OC=12，
∴△OAC是等边三角形，
∵B为母线OC的中点，
∴AB⊥OC，
∴AB=OA×sin60°=63．
（2）① 蚂蚁从点A爬行到点O的最短路径为：先沿着过A点且垂直于地面的直线爬到圆柱的上底面圆周上，再沿圆锥母线爬到顶点O上，因此，最短路径长为h+l
② 蚂蚁从点A爬行到点B的最短路径的示意图如下图所示，线段AB即为其最短路径（G点为蚂蚁在圆柱上底面圆周上经过的点，图中两个C点为图形展开前图中的C点）；
求最短路径的长的思路如下：如图，连接OG，并过G点作GF⊥AD，垂足为F，由题可知，OG=OC=l，GF=h， OB=b，
由AD的长为a，得展开后的线段AD=a，设线段GC的长为x，则GC的弧长也为x，由母线长为l，可求出∠COG，
作BE⊥OG，垂足为E，
因为OB=b，可由三角函数求出OE和BE，从而得到GE，利用勾股定理表示出BG，
接着由FD=CG=x，得到AF=a-x，利用勾股定理可以求出AG，
将AF+BE即得到AH，将EG+GF即得到HB，
因为两点之间线段最短，∴A、G、B三点共线，
利用勾股定理可以得到：AB2=AH2+BH2,进而得到关于x的方程，即可解出x，
将x的值回代到BG和AG中，求出它们的和即可得到最短路径的长．
【点睛】本题考查的是曲面上的最短路径问题，涉及到圆锥和圆柱以及它们的组合体上的最短路径问题，解题过程涉及到“两点之间、线段最短”以及勾股定理和三角函数等知识，本题为开放性试题，答案形式不唯一，对学生的空间想象能力以及图形的感知力要求较高，蕴含了数形结合等思想方法．
方法指导
当不易直接比较两个正数m与n的大小时，可以对它们的平方进行比较：
∵m2-n2=(m+n)(m-n)，m+n>0，
∴(m2-n2)与(m-n)的符号相同．
当m2-n2>0时，m-n>0，即m>n；
当m2-n2=0时，m-n=0，即m=n；
当m2-n2