2024~2025学年上海市九年级上学期期末模拟卷（一模）01数学试卷（解析版）

这是一份2024~2025学年上海市九年级上学期期末模拟卷（一模）01数学试卷（解析版），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
第Ⅰ卷
一、选择题:(本大题共6题，每题4分，共24分)
1．在中，，如果，，那么等于
A．B．C．D．
【答案】B
【解析】，
，
故选：B．
2．已知非零向量、、，下列条件中不一定能判定的是
A．B．
C．，D．，
【答案】A
【解析】由只能判定它们模的关系，不能判定方向关系，故选项符合题意，
选项、、一定能判定，
故选：．
3．已知：△△△，如果△与△的相似比为2，△与△相似比为4，那么△与△的相似比为
A．2B．4C．6D．8
【答案】D
【解析】△△△，如果△与△的相似比为2，△与△相似比为4
，，
设，则，
，
△与△的相似比为8．
故选：．
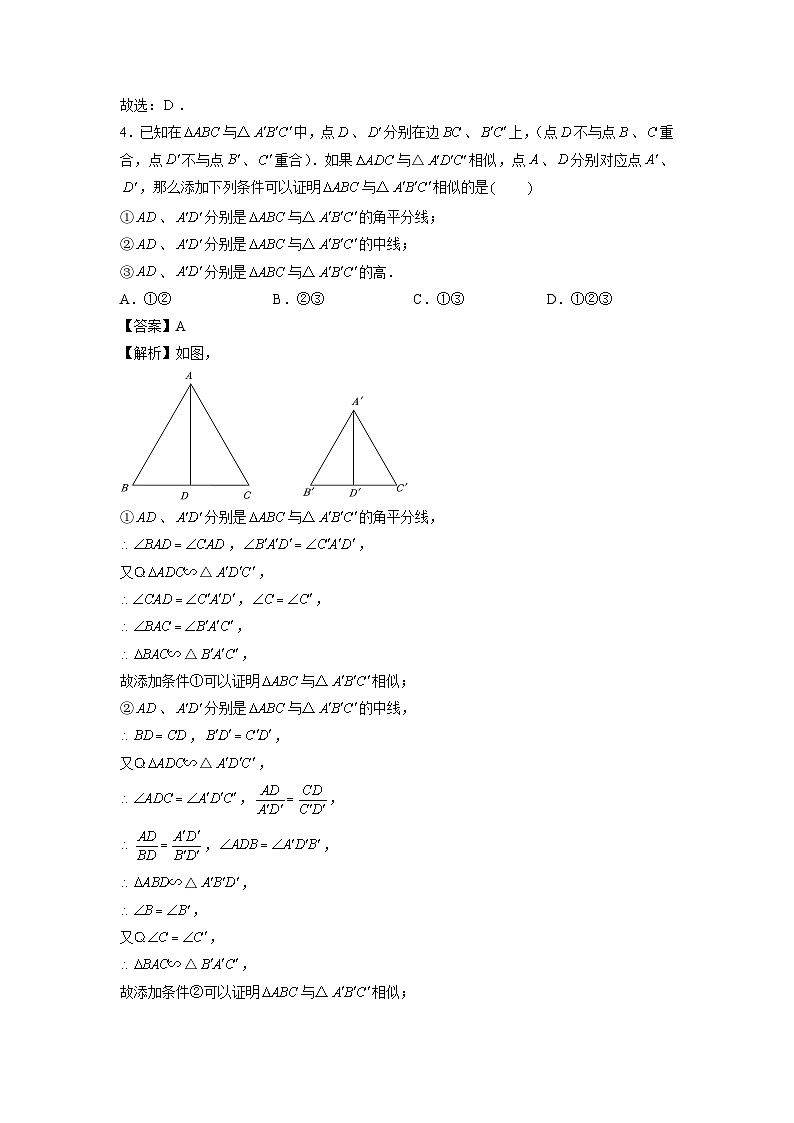
4．已知在与△中，点、分别在边、上，（点不与点、重合，点不与点、重合）．如果与△相似，点、分别对应点、，那么添加下列条件可以证明与△相似的是
①、分别是与△的角平分线；
②、分别是与△的中线；
③、分别是与△的高．
A．①②B．②③C．①③D．①②③
【答案】A
【解析】如图，
①、分别是与△的角平分线，
，，
又△，
，，
，
△，
故添加条件①可以证明与△相似；
②、分别是与△的中线，
，，
又△，
，，
，，
△，
，
又，
△，
故添加条件②可以证明与△相似；
③、分别是与△的高，△，
由图形可知，与△不相似，
故选：．
5．如图，△三边上点、、，满足，，那么下列等式中，成立的是
A．B．C．D．
【答案】B
【解析】、，
，，
△△，
，故错误；，
、，
四边形是平行四边形，
，，
，故正确；
，故错误；
，故错误，
故选：．
6．如图，二次函数的图象的顶点在第一象限，且过点和，下列结论：①：②；③；④当时，．其中正确结论的个数是
A．1个B．2个C．3个D．4个
【答案】C
【解析】由所给函数图象可知，，，，则．
故①②正确．
因为函数图象经过点，所以．故③正确．
由函数图象可知，
抛物线与轴有两个不同的交点，且抛物线开口向下，
所以当的取值在两个交点横坐标之间的时候（不包括端点），函数值大于零．
故④错误．
故选：．
第Ⅱ卷
二、填空题:(本大题共12题，每题4分，共48分)
7．已知，那么 ．
【答案】
【解析】，，
．
8．计算： ．
【答案】
【解析】．
9．已知线段，，那么线段、的比例中项等于 ．
【答案】
【解析】线段，，
线段、的比例中项．
故答案为：．
10．如图，，如果，，那么线段的长为 ．
【答案】6
【解析】，，
，；
故答案为：6．
11．已知线段，点是的黄金分割点，且，那么 ．
【答案】
【解析】线段，点是的黄金分割点，且，
，
故答案为：．
12．如图，某人沿着斜坡方向往上前进了30米，他的垂直高度上升了15米，那么斜坡的坡比 ．
【答案】
【解析】如图，过点作水平面于点，
米，米，
，，
斜坡的坡比，．
13．如图，已知，，，，那么用表示 ．
【答案】
【解析】连接交于，
，，
，，，，
，，，，
，，，，
．
14．抛物线的对称轴是直线，如果点、在此抛物线上，那么 ．（填“”、“ ”或“”
【答案】
【解析】抛物线的对称轴为直线，，
当时，随着的增大而增大．
，．
故答案为：．
15．如图，是线段上一点，，，，联结并延长交于点，联结并延长交于点．已知，，，，，那么 ．
【答案】1.6
【解析】，，
，
，
，，
，，，
，，，
设，则，
，，，
，，，
，，，解得：，
即，
故答案为：1.6．
16．“二鸟饮泉”问题中记载：“两塔高分别为30步和20步．两塔之间有喷泉，两鸟从两塔顶同时出发，以相同速度沿直线飞往喷泉中心，同时抵达．喷泉与两塔在同一平面内，求两塔之间的距离．”如图，已知，，是上一点，，在处测得点的俯角为，，，那么 ．
【答案】
【解析】由题知，
在点处测得点的俯角为，
．
在中，，
又，．
同理可得，．
又，．
在中，．
．
17．规定：平面上一点到一个图形的距离是指这点与这个图形上各点的距离中最短的距离．如图①，当时，线段的长度是点到线段的距离；当时，线段的长度是点到线段的距离；如图②，在中，，，，点为边上一点，，如果点为边上一点，且点到线段的距离不超过，设的长为，那么的取值范围为 ．
【答案】
【解析】过点作的垂线，交于点，
，，
，．
又，
，，则．
，在点的右侧存在到线段距离等于的点．
当且时，，则，
由勾股定理得，．
当点在点的左侧，且时，
过点作的垂线，垂足为，
由得，，，．
在△中，，
．．
18．如图，在中，，．点在边上，，点是射线上一动点，联结，将沿直线翻折，点落在点处，联结，如果，那么的长是 ．
【答案】6
【解析】过点作，，，垂足分别为、、，
，
，
．
，
设，，
，
，
，，
，
，
，
，
，
，，
，
，即与重合，
、、三点在同一直线上，
，
由折叠性质可知，，
，
，
，
故答案为：6．
三、解答题（本大题共7题，满分78分，10+10+10+10+12+12+14）
19．计算：．
解：原式
．
20．如图，在中，，，的平分线交边于点，点在边上，且，与相交于点．
（1）求的长；
（2）求的值．
解：（1），的平分线交边于点，
，，
，，
在中，，，
，
或（舍去），
；
（2）如图，过点作于点，
，
，
，
，，
，
，
，
故答案为：．
21．在平行四边形中，点是的中点，、相交于点．
（1）设，，试用、表示；
（2）先化简，再求作：（直接作在图中）．
解：（1）四边形是平行四边形，
，，
点是的中点，
，
，
，
，，
，
，
；
（2），
，，
如图，过点作交于点，连接，则即为所求．
22．如图①是某款智能磁吸键盘，如图②是平板吸附在该款设备上的照片，图③是图②的示意图．已知，，．当与形成的为时，求的长．（参考数据：，，；，，
解：过作于，
在中，，，
，，
在中，，，
，，
，
答：的长为．
23．已知：如图，在中，点、分别在边、上，与相交于点，，．
（1）求证：；
（2）如果，求证：．
（1）证明：，
，
，
，
．
，
，
，，
，
；
（2）解：，，
，
由（1）知：，
，
，
，
．
由（1）知：，
，
．
24．已知抛物线与轴交于、两点（点在点的左侧），与轴交于点，直线经过点与点．
（1）求抛物线的表达式；
（2）点在线段下方的抛物线上，过点作的平行线交线段于点，交轴于点．
①如果、两点关于抛物线的对称轴对称，联结，当时，求的正切值；
②如果，求点的坐标．
解：（1）直线经过点与点，
则点、的坐标分别为：、，
由题意得：，解得：，
则抛物线的表达式为：；
（2）①如图1，、两点关于抛物线的对称轴对称，
则轴，当时，则轴，
则，则；
②设点，如图2，
，，
则直线的表达式为：，
过点、分别作轴的垂线，垂足分别为点、，
，
则，
即，
则，
则点，，
将点的坐标代入抛物线表达式得：，
解得：，
则点．
25．在中，，，．点、分别在边、上，连接，将线段绕点按顺时针方向旋转得到线段．
（1）如图1，当点与点重合，时，与相交于点，求的值；
（2）如果（如图，当点、、在一条直线上时，求的长；
（3）如图3，当，时，连接，求的正切值．
解：（1）如图1，点与点重合，，
，
，
，
，，
，
由旋转得，，
，
，
，
，
的值为．
（2）如图2，作于点，则，
，，，，
，
，，
，，
，，
，
，，
点、、在一条直线上，，
，
，
，
，
，
整理得，
解得或，
的长是或．
（3）如图3，作于点，交的延长线于点，交于点，
，
，，
，，
，，
，，
，
，
，
，
，，
，
，
，
，
，，
，
，
的正切值为．