数学九年级下册第一章 直角三角形的边角关系4 解直角三角形评课ppt课件

这是一份数学九年级下册第一章 直角三角形的边角关系4 解直角三角形评课ppt课件，共49页。PPT课件主要包含了学习目标，新课探究，特殊角的三角函数值表，典例分析，归纳小结，巩固练习等内容，欢迎下载使用。
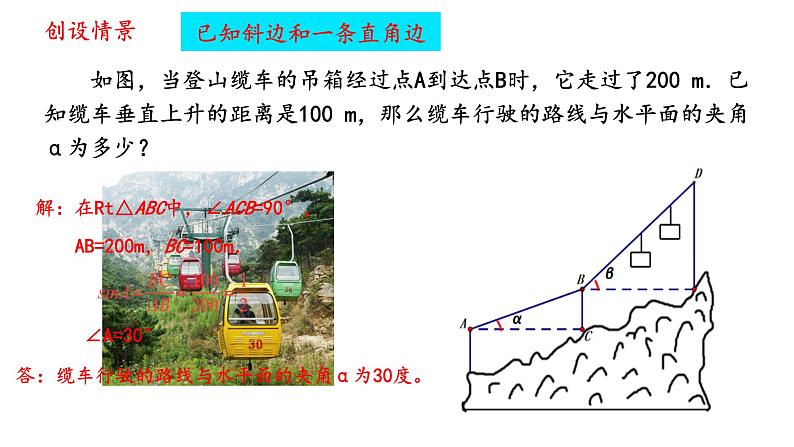
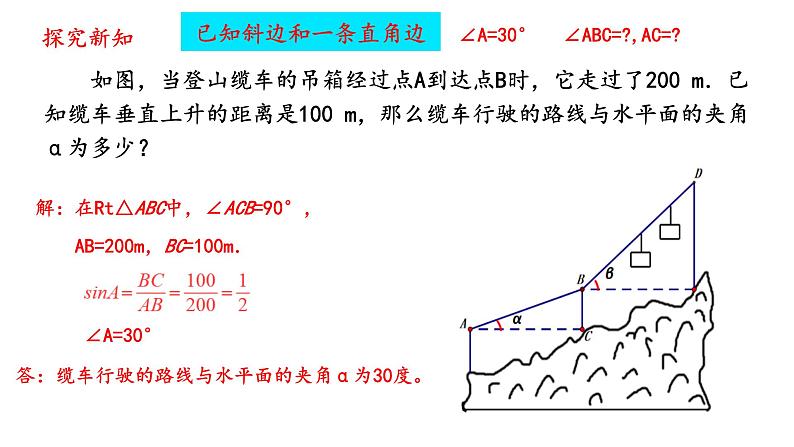
如图，当登山缆车的吊箱经过点A到达点B时，它走过了200 m．已知缆车垂直上升的距离是100 m，那么缆车行驶的路线与水平面的夹角α为多少？
解：在Rt△ABC中，∠ACB=90°， AB=200m，BC=100m．
答：缆车行驶的路线与水平面的夹角α为30度。
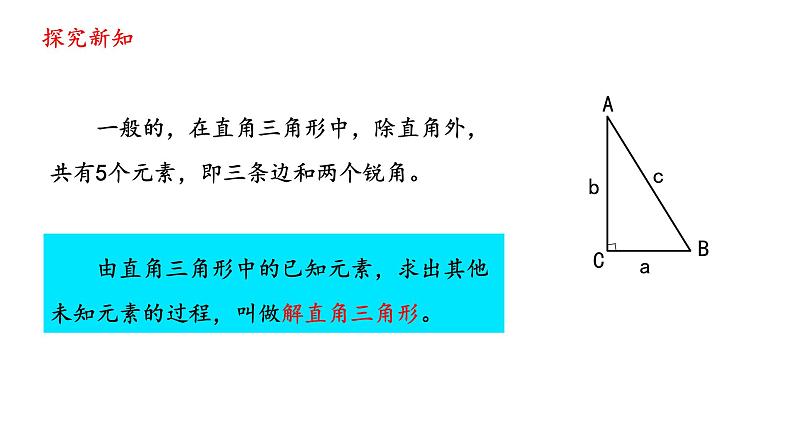
一般的，在直角三角形中，除直角外，共有5个元素，即三条边和两个锐角。
由直角三角形中的已知元素，求出其他未知元素的过程，叫做解直角三角形。
∠ABC=?,AC=?
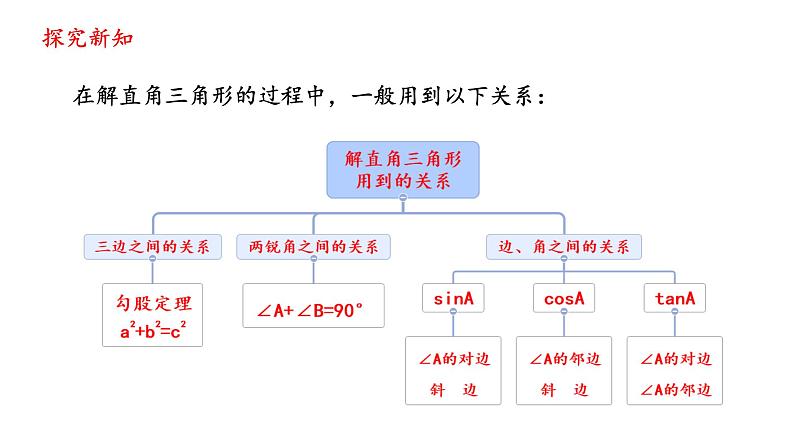
在解直角三角形的过程中，一般用到以下关系：
2.如图，在Rt△ABC中，∠B＝35°，b=20，解这个直角三角形。（精确到0.1）
解：∠A＝90°－∠B＝90°－35°＝55°
你还有其他的方法求c吗？
3.在本节课开始提出的问题中，当缆车继续由点B到达点D时，他又走过了200 m，缆车由点B到点D的行驶路线与水平面的夹角为∠β=42°，由此你还能计算什么？
解：在Rt△BDF中，∠BFD=90°， BD=200m，∠DBF=42°．
∠D＝90°－∠DBF＝90°－42°＝48°
已知一角一边可以解直角三角形，注意优化解题方法。
(1) 三边之间的关系:a2+b2=_____；
(2)锐角之间的关系：∠A+∠B=_____；
(3)边角之间的关系：sinA=_____，csA=_____，tanA=_____.
在Rt△ABC中，共有六个元素（三条边，三个角），其中∠C=90°，那么其余五个元素之间有怎样的关系呢？
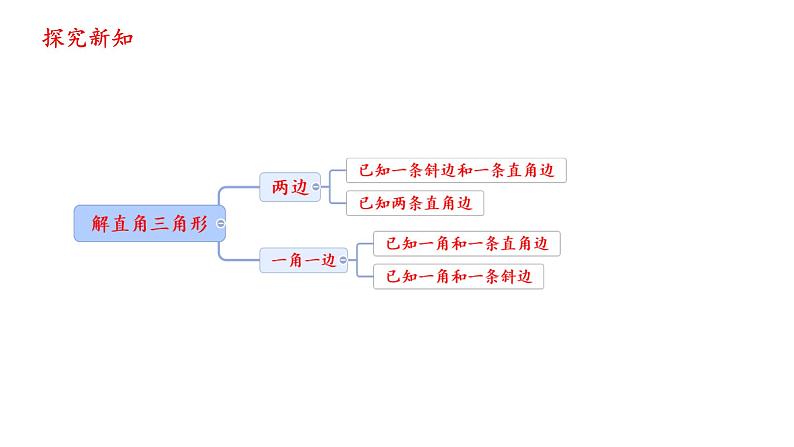
问题1 如果已知Rt△ABC中两边的长，你能求出这个三角形其他的元素吗？
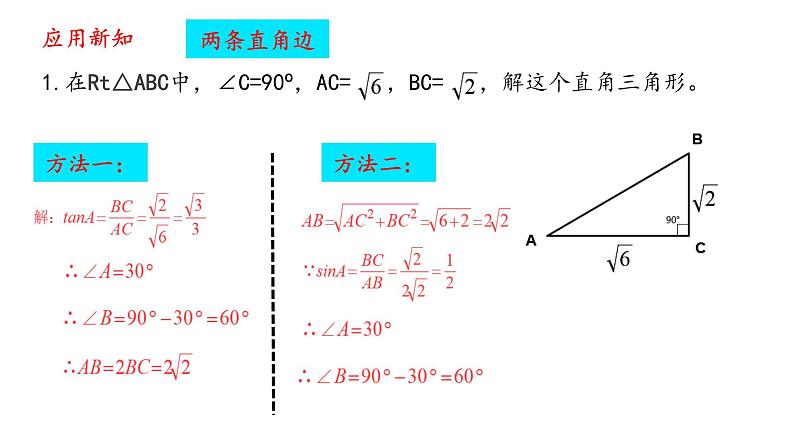
例1 如图，在Rt△ABC中，∠C＝90°，∠A，∠B，∠C所对的边分别为a，b，c，且 ,求这个直角三角形的其他元素.
解：在Rt△ABC中，a2+b2=c2,
在如图的Rt△ABC中，根据AC＝2.4，斜边AB＝6，你能求出这个直角三角形的其他元素吗？
问题2 如果已知Rt△ABC中一边和一锐角，你能求出这个三角形其他的元素吗？
例2 如图，在Rt△ABC中，∠C＝90°，∠A，∠B，∠C所对的边分别为a，b，c，且b=30，∠B＝25°,求这个直角三角形的其他元素(边长精确到1）.
在Rt△ABC中，∠C=90°，∠B=25°，
在图中的Rt△ABC中，根据∠A＝75°，斜边AB＝6，你能求出这个直角三角形的其他元素吗？
例3 如图，在△ABC中，∠B=30°，∠C=45°，AC=2，求BC.
如图，在菱形ABCD中，AE⊥BC于点E，EC=4， sinB＝ ，则菱形的周长是（　　） A．10 B．20 C．40 D．28
解直角三角形:在直角三角形中，由已知元素求未知元素的过程．
在解直角三角形的过程中，一般要用到下面一些关系：
要点精析：解直角三角形时，①已知两边求第三边用勾股定理；②已知一锐角求另一锐角用“直角三角形两锐角互余”；③在两边一锐角中，有两个元素已知，则可用三角函数的定义求出第三个元素． 由上可知在直角三角形的六个元素(三条边和三个角) 中，直角是已知元素，如果再知道一条边和第三个元素，就可以求出另外三个元素．3．解直角三角形时，选择三角函数关系式遵循以下原则： ①尽量选可以直接应用原始数据的关系式； ②尽量选择便于计算的关系式．如：当所求的元素既可 用乘法又可用除法求解时，一般用乘法，不用除法．4．易错警示：在直角三角形中寻找已知元素与未知元素的数量关系时，常建立三角函数模型研究边角之间的关系，注意正弦、余弦、正切三种函数都是涉及两边一角，要正确选择，不能将它们弄混．5. 解直角三角形的类型：（1）已知两边解直角三角形（2）已知一边及一锐角解直角三角形 已知两边解直角三角形 已知斜边和一条直角边解直角三角形
例2 已知在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边分别为a，b，c，且c＝5，b＝4，求这个三角形的其他元素．(角度精确到1′)
例3 在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边分别为a，b，c，且a＝1，b＝2.求这个三角形的其他元素．(角度精确到1′，边长精确到0.01)
已知一边及一锐角解直角三角形
在Rt△ABC中，如果已知一边和一个锐角，你能求出这个三角形的其他元素吗？
例4 在Rt△ABC，∠C=90°，∠A，∠B，∠C所对的边分别为a，b，c， 且b = 30, ∠B = 25°求这个三角形的其他元素（边长精确到1).
2.已知斜边和一锐角解直角三角形： 已知斜边和一锐角，则另一锐角易求．而求两直角边，必然要运用定义法，由斜边乘已知锐角的正弦可得已知锐角的对边；由斜边乘已知锐角的余弦可得已知锐角的邻边．当求出一直角边后，另一直角边也可用勾股定理计算，但要注意误差可能较大．
例5 在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边分别为a，b，c，且c＝100，∠A＝26°44′.求这个三角形的其他元素．(长度精确到0.01)
已知一边及一锐角的三角函数解直角三角形
导引：要求的BC边不在直角三角形中，已知条件中有∠B的正弦值，作BC边上的高，将∠B置于直角三角形 中，利用解直角三角形就可解决问题．
1.如图，在Rt△ABC中，∠C=90°，∠B=30°， AB=8，则BC的长是（　　）
2.在△ABC中，AB=AC=3，BC=4，则csB 的值是_________.
4.在Rt△ABC中，∠C＝90°，根据下列条件解直角三角形；（1）a = 30 , b = 20 ;
(2) ∠B＝72°，c = 14.
5. 如图，在Rt△ABC中，∠C＝90°，AC=6， ∠BAC的平分线 ，解这个直角三角形.
当△ABC为锐角三角形时，如图②，BC=BD+CD=12+5=17.
当△ABC为钝角三角形时，如图①，
∵AC=13，∴由勾股定理得CD=5
∴BC=BD-CD=12-5=7；
∴BC的长为7或17.
（2）两锐角之间的关系