初中数学1.不等式复习ppt课件

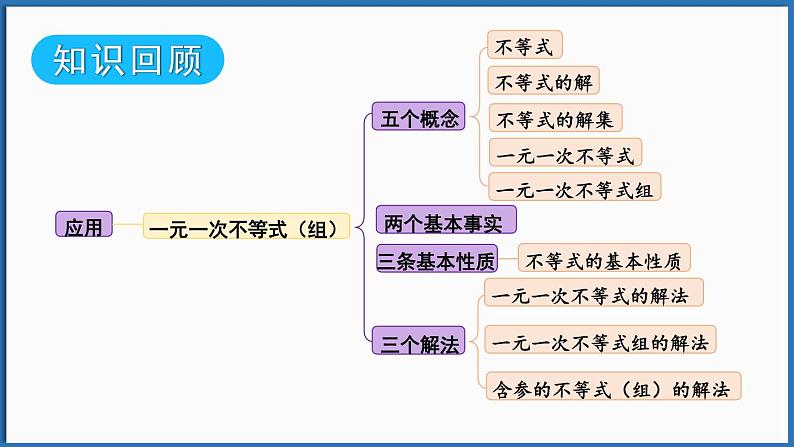
这是一份初中数学1.不等式复习ppt课件，共26页。PPT课件主要包含了+3＞5，x+y＞z，x–12，一元一次不等式，-4x3，①去分母，②去括号，③移项，④合并同类项，⑤系数化为1等内容，欢迎下载使用。
x = 1是不等式 x – 1  2的解
不等式 x – 1 2的解集是 x  3
用“≠”表示不等关系的式子也是不等式.
5. 一元一次不等式组
3x < 2x + 1
判断：1. 3b ≠ 1不是不等式. （ ）2. x + 2x + 3π < 1200是一元一次不等式. （ ）3. x = 2是不等式 x + 3 > 0的解. （ ）4. a 是负数表示为 a < 0. （ ）5. 不等式 3x > 6 的解集是 x > 2. （ ）6. 不等式 x + 3 > 0 的解集是 x = 2. （ ）7. 解集 0 < x < 3 的正整数解有 3 个. （ ）
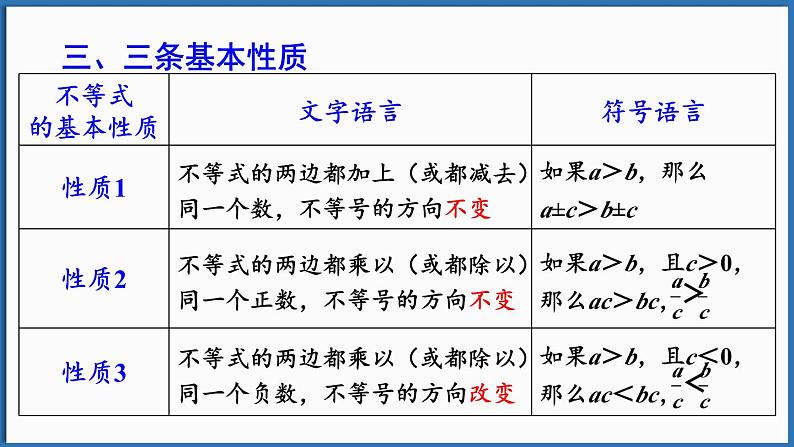
不等式的性质与等式的性质的不同点和相同点：
两边乘（或除以）同一个负数，不等号的方向改变
两边乘（或除以）同一个负数，结果仍相等
1.两边加（或减）同一个数（或式子），不等式和等式仍成立；2.两边乘（或除以）同一个正数，不等式和等式仍成立
练一练1. 如果 a＞b，下列不等式中，不成立的是（ ）A. a-3＞b-3 B. C. -2a＜-2b D. -2a＞-2b
2. 若a＜b，则下列不等式一定成立的是（ ）A. a-1＞b-1 B. a-b＜0 C. ma＜mb D. –a＜-b
1. 一元一次不等式的解法.
解不等式，并把解集在数轴上表示出来
2. 一元一次不等式组的解法.
解一元一次不等式组的步骤：
（1）求出各不等式的解集；（2）在数轴上表示各解集；（3）确定各解集的公共部分；（4）写出不等式组的解集.
解：解不等式①，得x > 2.
不等式的解集在数轴上表示如下：
解不等式②，得x  4.
所以不等式组的解集为2 < x  4.
关于 x 的不等式组 的解集为x＜3，求m的取值范围.
解：解不等式①，得x＜3，
∵原不等式组的解集为 x＜3，
解不等式②，得 x＜5-m.
2. 含参的不等式（组）的解法.
∴ 5 – m 3.
结合实例体会运用不等式解决实际问题的过程.
审：认真审题，分清已知量、未知量；
找：找出题目中的不等关系，抓住关键词， 如“超过”“不大于” “最多”等；
设：设出适当的未知数；
五、一元一次不等式（组）的应用
答：检验答案是否符合实际意义，并作答.
列：根据题中不等关系，列出一元一次不等式；
解：求出一元一次不等式的解集；
特别提醒：常见的不等式基本语言与符号表示：
老张与老李购买了相同数量的种兔，一年后，老张养兔数比买入种兔数增加了 2 只，老李养兔数比买入种兔数的 2 倍少 1 只，老张养兔数不超过老李养兔数的 ，一年前老张至少买了多少只种兔？
解：设一年前老张买了 x 只种兔，由题意得：2+x  （2x-1），解得 x  8.答：一年前老张至少买了 8 只种兔.
近年来新能源汽车产业及市场迅猛增长，为了缓解新能源汽车充电难的问题，某小区计划新建地上和地下两类充电桩，每个充电桩的占地面积分别为 3 m2 和1 m2. 已知新建地上充电桩与地下充电桩的数量与费用情况如下表:
（1）该小区新建一个地上充电桩和一个地下充电桩各需多少万元？（2）若该小区计划用不超过 16.3 万元的资金新建 60 个充电桩，且地下充电桩的数量不少于地上充电桩数量的 2 倍，则共有几种建造方案？请列出所有方案.
解：（1）设新建一个地上充电桩需要 x 万元，新建一个地下充电桩需要 y 万元.由题意得 解得答:新建一个地上充电桩需要 0.2 万元，新建一个地下充电桩需要 0.3 万元.
（2）设新建 m 个地上充电桩，则新建(60-m)个地下充电桩.由题意，得 解得 17  m  20. 因为 m 为正整数，所以 m 的值可以取17，18，19，20.所以一共有 4 种方案，分别为：方案一：新建 17 个地上充电桩，43 个地下充电桩；方案二：新建 18 个地上充电桩，42 个地下充电桩；方案三：新建 19 个地上充电桩，41个地下充电桩；方案四：新建 20 个地上充电桩，40个地下充电桩.