
2024-2025学年安徽省淮北市高三上学期第二次月考数学质量检测试题
展开
这是一份2024-2025学年安徽省淮北市高三上学期第二次月考数学质量检测试题,共4页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
第Ⅰ卷(选择题)
一、单选题(本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 已知集合,,,则( )
A. B. C. D.
2. 设复数,则的共轭复数在复平面内对应点的坐标为( )
A. B.
C. D.
3. 已知,,,则a,b,c的大小关系是( )
A B.
C. D.
4. 已知命题,,则的一个必要不充分条件是( )
A. B.
C. D.
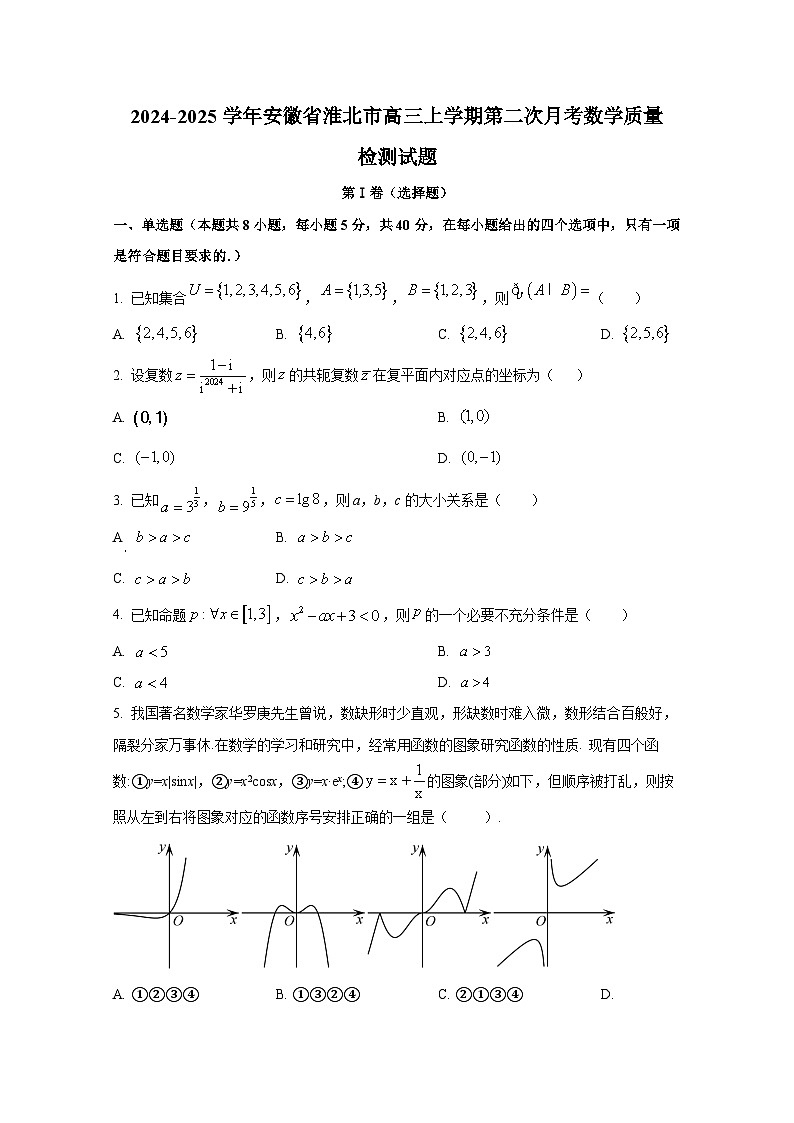
5. 我国著名数学家华罗庚先生曾说,数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,经常用函数的图象研究函数的性质. 现有四个函数:①y=x|sinx|,②y=x2csx,③y=x·ex;④的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是( ).
A. ①②③④B. ①③②④C. ②①③④D. ③②①④
6. 已知函数,若恰有两个零点,则正数的取值范围是( )
A. B. C. D.
7. 设函数,,若对任意的,存在,使得,则实数的取值范围是( )
A. B. C. D.
8. 已知函数.若,则实数的取值范围是( )
A. B. C. D.
二、多选题(本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求,全部选对得6分,部分选对的得部分分,有选错的得0分.)
9. 已知,,且,则下列说法正确的是( )
A B.
C. 的最小值为D.
10. 下列说法不正确的是( )
A. 已知,若,则组成集合为
B. 不等式对一切实数恒成立的充要条件是
C. 的定义域为,则的定义域为
D. 不等式解集为−∞,−2∪3,+∞,则
11. 设定义在上的函数与的导函数分别为和.若,,且为奇函数,则下列说法中一定正确的是( )
A. 函数的图象关于点对称
B.
C.
D.
第Ⅱ拳(非选择题)
三、填空题(本题共3小题,每小题5分,共15分.)
12. 已知幂函数在0,+∞上单调递减,则值为______.
13. 若函数存在单调递减区间,则实数的取值范围是________.
14. 函数.若对任意,都有,则实数m的取值范围为_________.
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演㑧步聚.)
15. 已知函数.
(1)若,求的取值范围;
(2)当时, 求函数的值域.
16. 如图,已知△ABC的内角A,B,C所对的边分别是a,b,c,.
(1)求角C:
(2)若,,延长CB至M,使得,求BM.
17. 如图,已知四棱锥的底面是边长为的正方形,,,是侧棱上的动点.
(1)若为的中点,证明平面;
(2)求证:不论点在何位置,都有;
(3)在(1)的条件下,求二面角的大小.
18. 已知函数.
(1)求曲线在处切线方程.
(2)求函数的极值;
(3)设函数.证明:存在实数,使得曲线关于直线对称.
19 已知函数.
(1)讨论的单调性;
(2)当时,求证;
(3)若有两个零点,求的取值范围.
相关试卷
这是一份2024-2025学年安徽省淮北市高三上册第二次月考数学质量检测试题(含解析),共16页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
这是一份安徽省淮南市和淮北市2024-2025学年高三上学期第一次质量检测数学试题,共4页。试卷主要包含了未知等内容,欢迎下载使用。
这是一份38,安徽省淮北市2024届高三第二次质量检测数学试题,共6页。试卷主要包含了考试结束后,将答题卡交回,已知A为双曲线E等内容,欢迎下载使用。








