2025高考数学考点剖析精创专题卷七-空间向量与立体几何【含答案】

这是一份2025高考数学考点剖析精创专题卷七-空间向量与立体几何【含答案】，共30页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。
1．某同学有一个形如圆台的水杯如图所示，已知圆台形水杯的母线长为，上、下底面圆的半径分别为和.为了防烫和防滑，水杯配有一个杯套，包裹水杯高度以下的外壁和杯底，如图中阴影部分所示，则杯套的表面积为（不考虑水杯材质和杯套的厚度）( )
A.B.C.D.
2．在《九章算术》中，将四个面都是直角三角形的四面体称为鳖臑.在鳖臑中，平面，，，，则此四面体的外接球表面积为( )
A.B.C.D.
3．已知l，m，n表示不同的直线，，，表示不同的平面，则下列四个命题正确的是( )
A.若，且，则B.若，，，则
C.若，且，则D.若，，，则
4．在正四棱台中，已知，，则侧棱与底面所成角的正弦值为( )
A.B.C.D.
5．在正方体中，E，F分别为AB，BC的中点，则( )
A.平面平面B.平面平面
C.平面平面D.平面平面
6．如图，在四棱锥中，底面ABCD是正方形，E是PD的中点，点F满足.若，，，则( )
A.B.C.D.
7．已知空间向量，，，若这三个向量共面，则实数等于( )
A.1
B.2
C.3
D.4
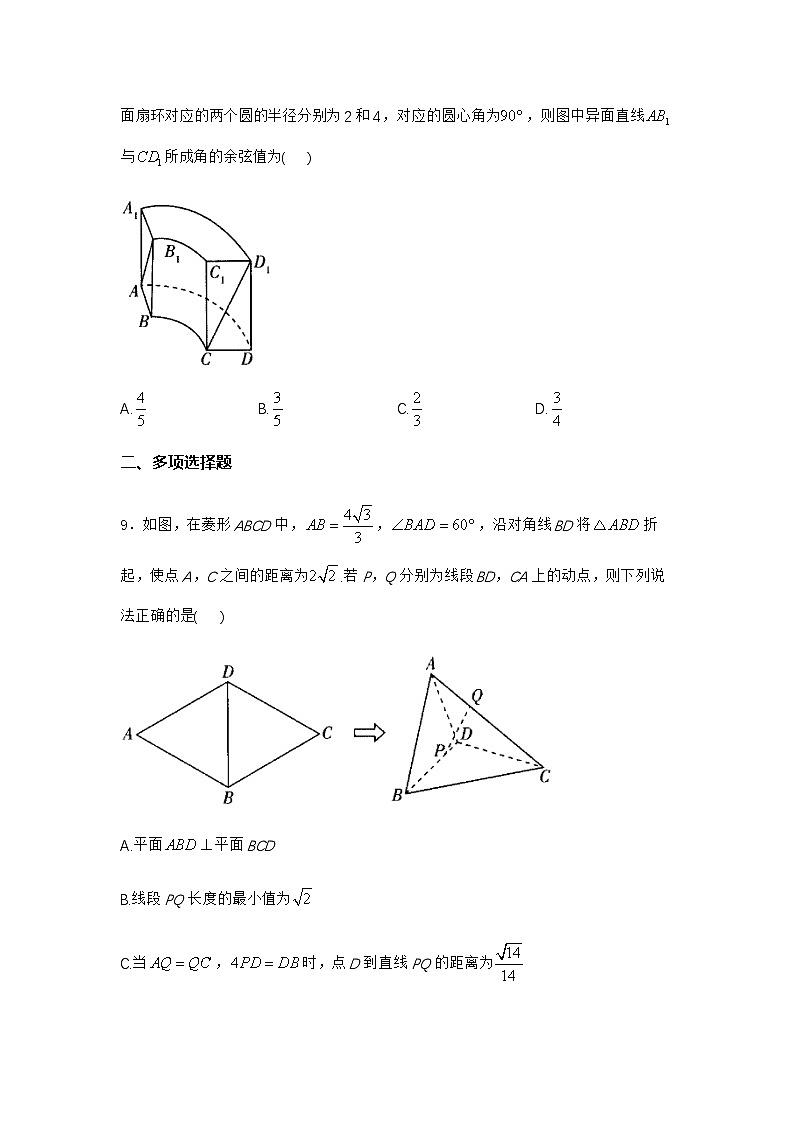
8．在中国古代数学著作《九章算术》中记载了一种称为“曲池”的几何体，该几何体的上、下底面平行，且均为扇环形（扇环是指圆环被扇形截得的部分）.现有一个如图所示的“曲池”，它的高为4，，，，均与“曲池”的底面垂直，底面扇环对应的两个圆的半径分别为2和4，对应的圆心角为，则图中异面直线与所成角的余弦值为( )
A.B.C.D.
二、多项选择题
9．如图，在菱形ABCD中，，，沿对角线BD将折起，使点A，C之间的距离为.若P，Q分别为线段BD，CA上的动点，则下列说法正确的是( )
A.平面平面BCD
B.线段PQ长度的最小值为
C.当，时，点D到直线PQ的距离为
D.当P，Q分别为线段BD，CA的中点时，PQ与AD所成角的余弦值为
10．如图，正方体的棱长为1，线段上有两个动点E，F，且，则下列结论正确的有( )
A.当点E运动时，总成立
B.当E向运动时，二面角逐渐变小
C.二面角的最小值为
D.三棱锥的体积为定值
11．已知在直三棱柱中，底面是一个等腰直角三角形，且，E，F，G，M分别为，，，的中点，则( )
A.与平面夹角的余弦值为
B.与的夹角为
C.平面EFB
D.平面平面
三、填空题
12．在正方体中,E是的中点,求与两条异面直线所成角的余弦值为______________.
13．已知平面四边形ABCD中，点B，D在线段AC两侧，且线段AC的垂直平分线为直线BD，其中，，现沿BD进行翻折，使得点A到达点的位置，且A′到C的距离为3，连接，，，则四面体体积的最大值为_____________.
14．如图，由直三棱柱和四棱锥构成的几何体中，，，，，平面平面.P为线段BC上一动点，当_________时，直线DP与平面所成角的正弦值为.
四、解答题
15．如图，在三棱锥中，平面平面，，O为BD的中点.
（1）证明：；
（2）若是边长为1的等边三角形，点E在棱AD上，，且二面角的大小为，求三棱锥的体积.
16．已知直三棱柱中，侧面为正方形，，E，F分别为AC和的中点，D为棱上的点，.
（1）证明：；
（2）当为何值时，面与面DFE所成的二面角的正弦值最小？
17．如图，四面体ABCD中，，，，E为AC的中点.
（1）证明：平面平面ACD；
（2）设，，点F在BD上，当的面积最小时，求CF与平面ABD所成的角的正弦值.
18．在如图所示的试验装置中，两个正方形框ABCD，ABEF的边长都是1，且平面平面ABEF，活动弹珠（大小不计）M，N，G分别在线段AC，BF，AB上移动，，平面MNG，记.
（1）证明：平面ABEF；
（2）当MN的长度最小时，求二面角的余弦值.
19．如图①，已知三棱锥，图②是其平面展开图，四边形ABCD为正方形，和均为正三角形，O，G分别为AC，PA的中点，.
（1）求证：；
（2）求二面角的余弦值；
（3）若点M在棱PC上，满足，，点N在棱BP上，且，求的取值范围.
参考答案与详细解析
一、选择题
1．答案：C
解析：根据题意，杯套的形状可看作一个圆台，且该圆台的母线长是圆台形水杯的母线长的，即，下底面圆的半径为圆台形水杯的下底面圆的半径，即，上底面圆的半径是，所以杯套的表面积.故选C.
2．答案：B
解析：根据题意，平面，平面，所以，
又，，平面，所以平面，
将鳖臑补全成长方体，如图，
则此四面体的外接球的半径为，
其外接球的表面积为.
故选：B.
3．答案：C
解析：若，且，则l与m可能平行，可能相交，可能异面，A选项错误；
若，，，则m与n可能平行，可能相交，可能异面，B选项错误；
两条平行直线，其中一条与平面垂直，则另一条也与平面垂直，C选项正确；
若，，，则与可能平行可能相交，D选项错误.
故选：C
4．答案：B
解析：
由题意可得正四棱台的截面图，如图所示，且为等腰梯形，过点做，过点做，由线面角的定义可知，侧棱与底面所成角即为，
由条件可得，，,，则，,则，所以为等腰直角三角形，
所以，即.
故选：B.
5．答案：A
解析：对于A选项：在正方体中，因为E，F分别为AB，BC的中点，所以，则有，又由正方体的性质可得，又，从而平面.又因为平面，所以平面平面，所以A选项正确.
对于B选项：因为平面平面，由选项A知平面平面，若平面平面，则平面，显然不成立，所以B选项错误.
对于C选项：由题意知直线与直线必相交，故平面与平面有公共点，所以C选项错误.
对于D选项：如图，连接，，，易知平面平面，
又因为平面与平面有公共点，故平面与平面不平行，所以D选项错误.故选A.
6．答案：C
解析：由题意知
.
故选C.
7．答案：A
解析：由题意得，存在实数x，y，满足，即，所以解得故实数等于1.
8．答案：A
解析：设上底面圆心为，下底面圆心为O，连接，，，，，
以O为原点，分别以，，所在直线为x轴、y轴、z轴，建立空间直角坐标系，则，，，，则，.
所以，
又异面直线所成角的范围为，故异面直线与所成角的余弦值为.故选A.
二、多项选择题
9．答案：ABD
解析：取BD的中点O，连接OA，OC.在菱形ABCD中，，，所以.
因为，所以，所以.
又因为，O为BD的中点，所以，同理可得，
因为，，，平面BCD，所以平面BCD.
因为平面ABD，所以平面平面BCD，故A正确.
又，，，故以O为原点，OB，OC，OA所在直线分别为x，y，z轴建立如图所示的空间直角坐标系，
则，，，.
当，时，，，，，
所以点D到直线PQ的距离为，故C错误.
设，，设，，得，，
当且时，，故B正确.
当P，Q分别为线段BD，CA的中点时，，，，，
设PQ与AD所成的角为，则，
所以PQ与AD所成角的余弦值为，故D正确.故选ABD.
10．答案：ACD
解析：对于A，连接，，.
因为四边形为正方形，所以，
因为平面，平面，所以，
又，平面，所以平面.
又因为平面，所以，同理可证.
又因为，平面，所以平面，又因为平面，所以总成立，故A正确.
对于B，连接BD，平面EFB即平面，平面EFA即平面，所以当E向运动时，二面角的大小不变，故B错误.
对于C，建立如图所示的空间直角坐标系，
则，，
所以，
因为E，F在上，且，
故可设，，，则，
由题易知平面ABC的一个法向量为，
设平面ABE的法向量为，则
取，则，，故，设二面角的平面角为，则为锐角，
所以，又，所以当时，取得最大值，取得最小值，故C正确.
对于D，因为，点A到平面EFB的距离即为点A到平面的距离，为，所以，为定值，故D正确.故选ACD.
11．答案：BCD
解析：如图①，以B为原点，BC，，所在直线分别为x轴，y轴，z轴，建立空间直角坐标系，设，则有，，，，，，，，，，.
设平面的法向量为，则有令，可得平面的一个法向量为，则，
与平面夹角的正弦值为，则余弦值为，A错误.
，与的夹角的余弦值为，则其夹角为，B正确.
如图②，连接，，设，连接，，M分别为，的中点，且，为平行四边形，则O为的中点.
又为的中点，，又平面，平面，平面，C正确.
连接，如图②，由题可知平面即为平面，且，，又，平面，平面，又平面，则，又四边形为正方形，则，又，平面，所以平面，又平面，平面平面，即平面平面，D正确.故选BCD.
三、填空题
12．答案：
解析：如图,取的中点,连接,,,
则,,所以,且,
故四边形是平行四边形,
则,故即为与所成角（或其补角）,
设正方体的棱长为2,由勾股定理得,,
在中,由余弦定理得,
故与两条异面直线所成角的余弦值为.
故答案为：.
13．答案：
解析：如图，，，所以A点在以B，D为焦点，长轴长为15的椭圆上，该椭圆中：，，即，，因此，
由椭圆性质知A点到直线的距离的最大值为，
设与交于点O，因为，即，，
又，，平面，所以面，
，
，因此，而，因此，
，
所以时，取得最大值，
即取得最大值.
故答案为：.
14．答案：1
解析：以A为坐标原点，，，的方向分别为x，y，z轴的正方向建立空间直角坐标系.
则，，，，，所以，.
设平面的法向量，所以
所以
取，可得平面的一个法向量，设，，所以，所以解得或（舍去），所以.
因为，所以.
四、解答题
15．答案：（1）证明见解析
（2）
解析：（1）证明：因为，O为BD的中点，所以.
又平面平面，平面ABD，平面平面，
所以平面BCD.又平面BCD，所以.
（2）如图，取OD的中点F，连接CF，则.
过点O作交BC于点G，则.所以OG，OD，OA两两垂直.
以点O为坐标原点，分别以OG，OD，OA所在直线为x，y，z轴建立空间直角坐标系Oxyz，如图所示，
则，，，.
设，，又，则，所以，.
设平面BCE的法向量为，
则
令，则，，所以.
易知平面BCD的一个法向量为，因为二面角的大小为，
所以.
又，得，即，
所以
16．答案：（1）证明见解析
（2）
解析：（1）因为E，F分别是AC和的中点，且，
所以，.
连接AF，由，，得，
于是，
所以.
由，得，
故以B为坐标原点，以，，的方向分别为x，y，z轴的正方向建立空间直角坐标系，
则，，，.
设，则，
于是.
所以，所以.
（2）平面的一个法向量为.
设面DFE的一个法向量为，，，
则，所以，
令，得，，
所以，
所以.
设面与面DFE所成的二面角为，
则，
故当时，面与面DFE所成的二面角的正弦值最小，为，
即当时，面与面DFE所成的二面角的正弦值最小.
17．答案：（1）证明见解析
（2）
解析：（1）证明：因为在和中，，，，
所以，所以.
又因为E为AC的中点，所以.
因为，E为AC的中点，所以.
又，所以平面BED.
又因为平面ACD，所以平面平面ACD.
（2）由（1）得，又，所以为等边三角形.
因为，所以，.
因为，，
所以是等腰直角三角形，所以，.
因为，所以，
于是在中，设h为的边BD的高，
则由等面积可得，即.
连接EF，由（1）知平面BED，
又平面BED，所以，于是当时，的面积最小，
此时，，，
所以此时F为线段BD上靠近点D的四等分点.
以E为坐标原点建立如图所示的空间直角坐标系，
则，，，，，，
所以，，.
设平面ABD的法向量为，
则即，令，则.
所以，
故直线CF与平面ABD所成的角的正弦值为.
18．答案：（1）证明见解析
（2）
解析：（1）证明：因为平面MNG，且平面ABEF，
平面平面，
所以.
因为，
所以，
则，，
即，所以.
因为，所以，
又平面平面ABEF，平面平面，平面ABCD，
所以平面ABEF.
（2）由（1）知，平面ABEF，
因为平面ABEF，所以，
所以，
当且仅当时，等号成立.
所以当MN的长度最小时，，G为AB中点.
以点B为坐标原点，BA，BE，BC所在直线分别为x，y，z轴建立如图所示的空间直角坐标系，
则，，，，
则，，.
设平面AMN的法向量为，则
取，可得.
设平面BMN的法向量为，则
取，可得.
所以，
由图可知，二面角为钝角，故二面角的余弦值为.
19．答案：（1）证明见解析
（2）
（3）
解析：（1）证明：因为O，G分别为AC，PA的中点，
在中，，，所以.
（2）如图①，连接GB，OB，
在等边中，，又，所以为二面角的平面角.
又，所以，，，
所以，所以，所以，
所以二面角的余弦值为.
（3）如图②，过点N作交CP于点Q，
因为，所以.因为，所以.
在中，根据余弦定理，得，所以.
设，所以，，，
在中，根据余弦定理得，.
因为，所以.
在中，，
在中，，得，
又，所以，
即的取值范围为，的取值范围为